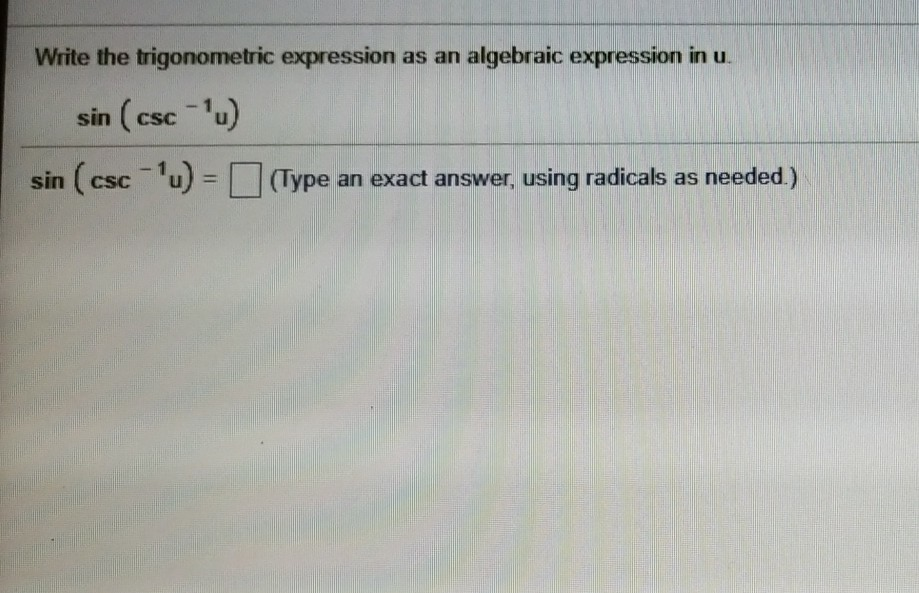
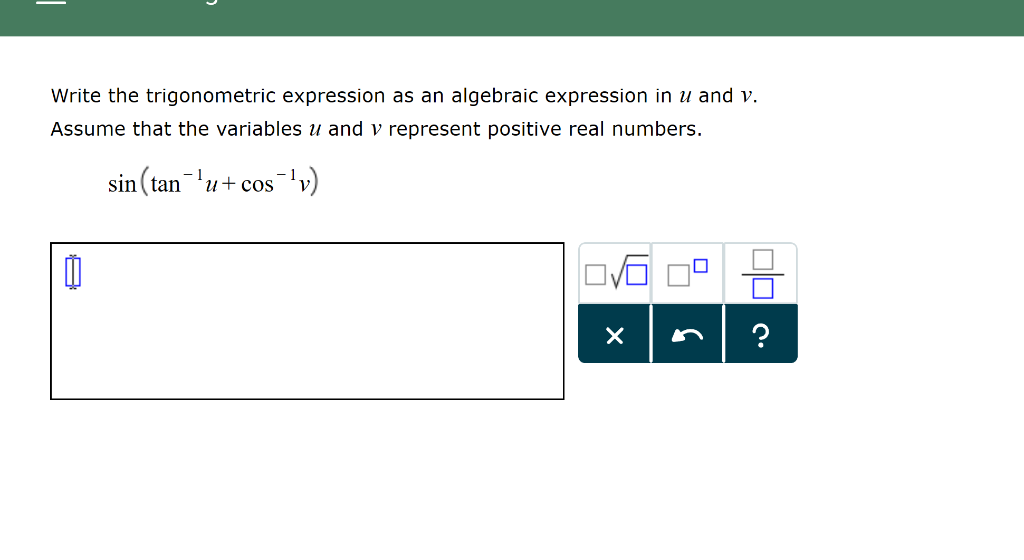
Write The Trigonometric Expression As An Algebraic Expression In U
Hey there, fellow curious minds! Ever stumbled across a math problem that looked like it was written in some secret ancient language? You know, the kind with a bunch of sin(), cos(), and tan() symbols doing a dizzying dance? Well, today, we're going to demystify one of those situations. Specifically, we're going to chat about how to take a trigonometric expression – the fancy math word for stuff involving those trig functions – and turn it into a nice, neat algebraic expression, which is basically just an expression with numbers, variables (like our friend 'u'), and arithmetic operations (+, -, *, /).
Think of it like this: Imagine you're looking at a beautiful, intricate stained-glass window. It's stunning, right? But sometimes, you might want to understand the underlying structure, the way the different colored pieces fit together to create that masterpiece. Trigonometric expressions are a bit like those windows – beautiful and descriptive, but sometimes we want to see the basic building blocks. And converting them to algebraic expressions in terms of 'u' is like understanding those building blocks.
So, what's the big deal? Why would we even bother doing this? Well, sometimes, working with algebraic expressions is just plain easier. They're often simpler to manipulate, substitute values into, or integrate (if you're into calculus!). It's like switching from trying to measure something with a protractor and compass to just using a ruler. It gets the job done more directly.
Our star player in this transformation is usually something like sin(θ) or cos(θ), where 'θ' (theta) is an angle. But sometimes, instead of a simple angle, we have something a bit more complex, like sin(2θ), or even sin(θ/2), or maybe even a mix like sin(θ)cos(θ). The problem asks us to express these in terms of a single variable, 'u'. Usually, this 'u' is related to one of the trigonometric functions of our original angle. For example, a common scenario is when we're asked to express something in terms of u = sin(θ), or perhaps u = cos(θ).
Let's dive into a common scenario. Suppose we have an expression like sin(2θ) and we want to write it in terms of u = sin(θ). How do we do that? Well, math has these handy little tools called trigonometric identities. These are like secret codes or shortcuts that tell us how different trigonometric functions are related. One of the most famous identities is the double angle formula for sine, which states: sin(2θ) = 2sin(θ)cos(θ).

Aha! See what happened there? We've got sin(θ) in the formula, which is our 'u'. But we also have cos(θ). So, we're not quite there yet. We need to get rid of that cos(θ) and express it in terms of 'u' as well. This is where another fundamental identity comes to the rescue: the Pythagorean identity. This one says: sin²(θ) + cos²(θ) = 1.
From the Pythagorean identity, we can rearrange it to solve for cos²(θ): cos²(θ) = 1 - sin²(θ). Now, if we take the square root of both sides, we get cos(θ) = ±√(1 - sin²(θ)). Notice the 'plus or minus' there? That's important! The sign of cosine depends on which quadrant the angle 'θ' is in. But for many problems, we might be given a specific range for 'θ' that clarifies the sign, or we might be asked for a general expression where the ± is included.
Now, let's put it all together. We had sin(2θ) = 2sin(θ)cos(θ). We know sin(θ) = u. And we know cos(θ) = ±√(1 - sin²(θ)). So, substituting 'u' in, we get cos(θ) = ±√(1 - u²). Therefore, sin(2θ) = 2 * u * (±√(1 - u²)). Which simplifies to sin(2θ) = ±2u√(1 - u²).
Isn't that neat? We took something that looked purely trigonometric and turned it into an algebraic expression involving only 'u' and some basic operations and a square root. It's like taking a beautiful painting and being able to describe it using just a few primary colors and geometric shapes.
Let's try another one to solidify this. What if we wanted to express cos(2θ) in terms of u = cos(θ)? There are actually a few versions of the double angle formula for cosine. One of them is: cos(2θ) = 2cos²(θ) - 1.

This one is even more straightforward! If we let u = cos(θ), then cos²(θ) = u². So, substituting directly into the formula, we get cos(2θ) = 2u² - 1. Boom! Done. No square roots, no plus-or-minus. Just a simple quadratic expression in 'u'. It’s like finding a shortcut on a road trip; sometimes the most complex-looking route turns out to have a surprisingly simple bypass.
What about something like tan(θ) if we know u = sin(θ)? We know that tan(θ) = sin(θ) / cos(θ). We already figured out that cos(θ) = ±√(1 - sin²(θ)). So, substituting 'u' for sin(θ), we get tan(θ) = u / (±√(1 - u²)). Or, we could write it as tan(θ) = ±u / √(1 - u²).
The key takeaway here is that these trigonometric identities act as our translators. They allow us to swap out trigonometric functions for their algebraic equivalents, using our chosen variable 'u'. It's all about understanding the relationships between the different trigonometric functions.

Why else is this useful? Imagine you're trying to solve a complex equation that involves both trigonometric and algebraic terms. Sometimes, transforming all the trigonometric parts into algebraic ones can make the equation much simpler to solve. It’s like clearing the table of clutter before you start a big project; once everything is in one place and in a consistent format, it’s much easier to tackle.
So, the next time you see a trigonometric expression that needs to be converted into an algebraic one in terms of 'u', don't sweat it! Remember the power of trigonometric identities. They are your best friends in this quest. Think of them as your magic wand, allowing you to transform the seemingly complex into the elegantly simple.
It's a bit like learning to read sheet music. At first, those little notes on the lines can look like a jumble. But once you learn the rules, the relationships between the notes, and how they form chords and melodies, you can understand and even create entire symphonies. Similarly, understanding these trigonometric-to-algebraic transformations opens up a whole new level of understanding and manipulation in mathematics. It's a fundamental skill that unlocks doors to solving more advanced problems and appreciating the interconnectedness of mathematical concepts. Pretty cool, right?
