Write An Equation For The Hyperbola With The Given Characteristics

Ever wondered what makes a satellite dish curve just so, or why a fountain’s arc looks so graceful? It all comes down to fascinating shapes, and today we're diving into one of the coolest: the hyperbola! Don’t let the fancy name scare you; understanding hyperbolas is actually a lot of fun and surprisingly useful. Think of it as unlocking a secret code to understand some of the elegant curves we see all around us.
So, what’s the point of writing an equation for a hyperbola? Well, for beginners, it’s a fantastic way to build foundational math skills in a visually interesting way. You’re not just crunching numbers; you’re describing a shape! For families, it can be a fun way to connect abstract math concepts to real-world objects. Imagine sketching out a hyperbola and then finding examples in your own home or neighborhood – it turns learning into a treasure hunt! And for hobbyists, whether you're into 3D printing, design, or even astronomy, understanding hyperbolic shapes can open up new creative possibilities. Knowing how to write the equation is like having the blueprint to design or analyze these intriguing curves.
Let’s look at how we might describe a hyperbola. Imagine you're given a couple of key pieces of information. For instance, you might be told where the center of the hyperbola is and the locations of its foci. The foci are like special points that guide the shape of the hyperbola. Another way to define it is by its vertices (the points where the hyperbola is closest to its center) and its asymptotes. Asymptotes are lines that the hyperbola gets closer and closer to but never actually touches – like a racehorse that can run alongside a track but never quite reaches the finish line!
For example, if we’re told a hyperbola is centered at the origin (0,0) and its vertices are at (3,0) and (-3,0), and its foci are at (5,0) and (-5,0), we can start building its equation. This is a standard hyperbola that opens left and right. If, however, the vertices were at (0,3) and (0,-3) and the foci at (0,5) and (0,-5), it would be a hyperbola opening up and down. The specific numbers and their positions are what dictate the exact equation.
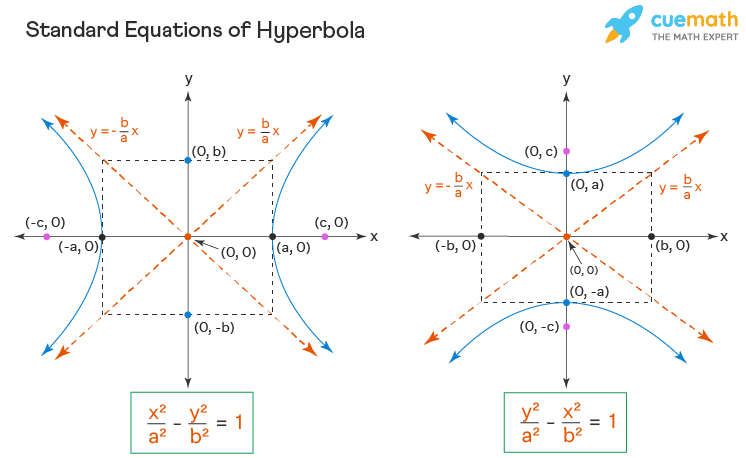
Getting started with writing hyperbola equations is simpler than you might think. First, visualize the shape. Is it opening left and right, or up and down? This will tell you which variable (x or y) will be positive in your equation. Next, identify the center. If it’s not at (0,0), you’ll need to adjust your equation accordingly. Then, figure out the distances related to the vertices and foci. These distances are crucial for plugging into the standard formula. Don't be afraid to sketch it out! A simple drawing can make a huge difference in understanding the relationships between the different parts of the hyperbola.
Writing an equation for a hyperbola might seem like a purely academic exercise, but it’s a gateway to appreciating the mathematical beauty of curves and their presence in our world. It’s a rewarding process that combines logic and visualization, leading to a deeper understanding and enjoyment of mathematics.
