Write An Equation For The Hyperbola Shown In The Graph
Alright folks, settle in, grab your lattes, and let's talk about something that sounds super fancy but is actually, dare I say, kind of a blast. We're diving headfirst into the wild, wacky world of hyperbolas. Yeah, I know, it sounds like something you'd get from a mad scientist's lab or a particularly difficult exam question. But trust me, these things are cooler than a penguin in a snowsuit.
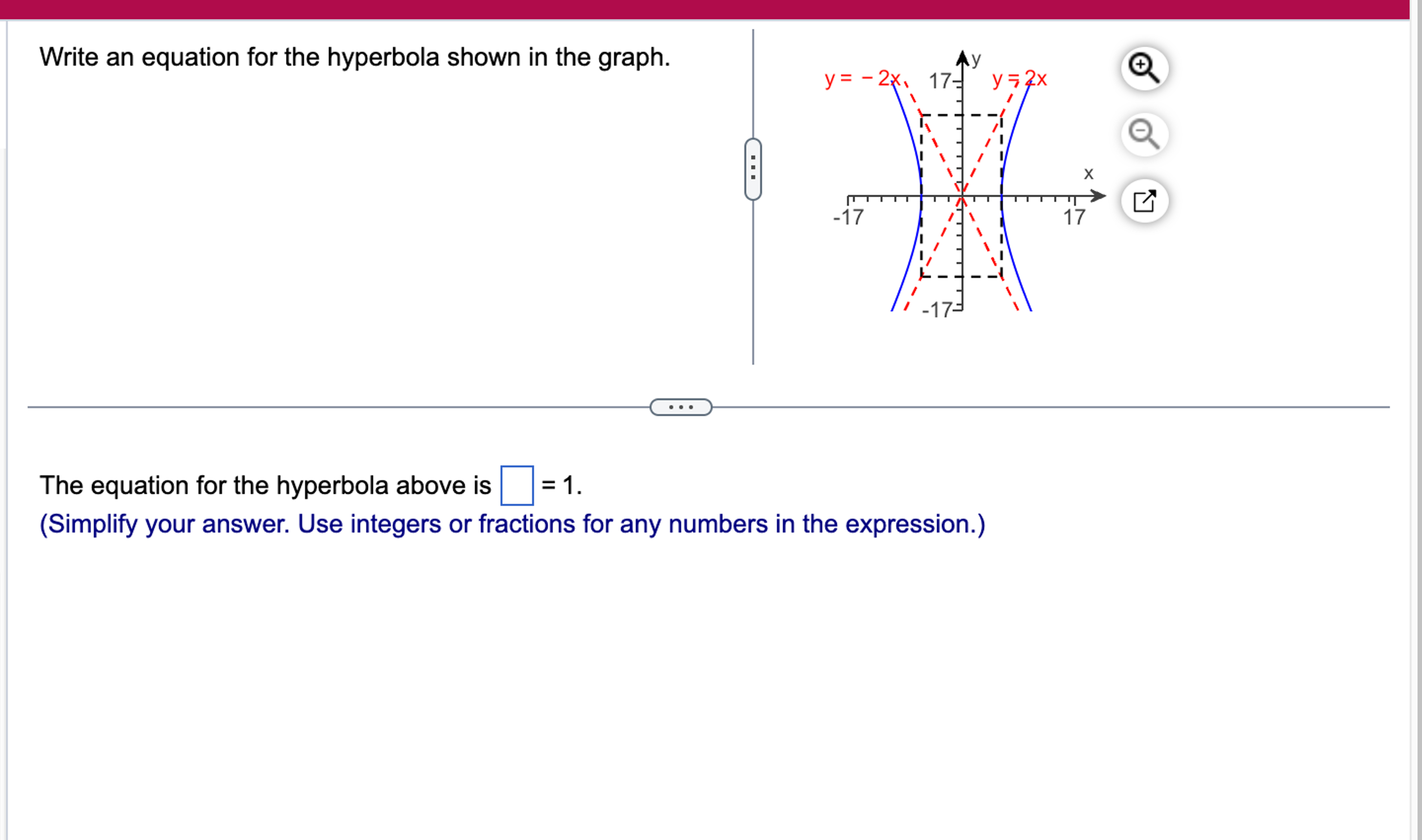
So, imagine you're at a coffee shop, right? And this is the coffee shop. This is our visual feast, our graph of doom (or delight, depending on your math tolerance). We've got these two swooshing, curving lines that look like they're trying to escape each other, or maybe they're just having a really intense staring contest. They're like the Romeo and Juliet of conic sections, destined to be apart but forever defined by their relationship.
Now, our mission, should we choose to accept it (and we will, because we're brave mathematicians-in-training), is to write an equation for this bad boy. Think of it as giving this beautiful, sassy hyperbola a name. And not just any name, but a mathematical name that tells us exactly how it's shaped, where it lives, and how it behaves. It's like its astrological chart, but with numbers.
The Anatomy of a Hyperbola
Before we write its autobiography, let's get to know our hyperbola. We need to identify its key features, the parts that make it tick. First up, we have the center. This is the grumpy old man of the hyperbola, the point right in the middle from which everything else radiates. Looking at our graph, it seems to be chilling right at the origin, that cozy little (0,0) spot. Easy peasy, lemon squeezy!
Next, we need to talk about the vertices. These are the points where the hyperbola actually turns. They're like the hyperbola's elbows, the sharpest points of its curve. On our graph, these vertices are sitting pretty on the x-axis. One's at (-3, 0) and the other is at (3, 0). See? They're perfectly symmetrical, like twins who always wear matching outfits.
The distance from the center to each vertex is super important. It's like the hyperbola's arm span. In this case, that distance is 3. We call this magical number 'a'. So, a = 3. Remember that. It's a key piece of our puzzle.

Now, there's another crucial element, something that makes hyperbolas so… hyperbolic. They have these things called asymptotes. These are imaginary lines that the hyperbola's arms chase forever, getting closer and closer but never, ever touching. It's like trying to hug a ghost – you get really close, but there's always that invisible barrier. They’re the ultimate "it's complicated" relationship status of the math world.
On our graph, these asymptotes are these dashed lines zipping through the center. One goes up and to the right, and the other goes down and to the right. They form a sort of X-shape. To find the equations of these asymptotes, we need something else: the distance from the center to the points called co-vertices. But wait, we don't have co-vertices explicitly marked on our graph! What gives?
Here's where things get a little detective-y. For a hyperbola that opens left and right (like ours does, with the vertices on the x-axis), the standard equation looks like this: (x²/a²) - (y²/b²) = 1. Notice the minus sign in the middle. That's what makes it a hyperbola and not a smug ellipse. Elipses are all about unity and closeness; hyperbolas are about dramatic separation.
The asymptotes for this type of hyperbola have equations of the form y = ±(b/a)x. We know 'a' is 3. We need 'b'. How do we find 'b' if it's not directly on the graph? Sometimes, the graph gives us enough clues, or we might need another piece of information, like the location of the foci. The foci are like the hyperbola's secret crushes, the points that define its shape. But alas, no foci are shown here.
However, and this is a big "however" – a capitalized, underlined, glitter-bombed "however" – sometimes the graph is drawn in such a way that we can infer the 'b' value by looking at the steepness of the asymptotes. If you look really, really closely at those dashed lines, they seem to go up 2 units for every 3 units they go across. That means the slope of the asymptotes is ±2/3. Aha! Since the asymptote equation is y = ±(b/a)x, and we know a=3, then b/a must equal 2/3. So, b/3 = 2/3. Multiply both sides by 3, and what do you get? b = 2! Boom!
Putting It All Together
So, we've got our ingredients: * Center: (0,0) * Vertices: (±3, 0) -> This means a = 3 * Asymptotes: y = ±(2/3)x -> This means b = 2
Now, let's plug these into our standard hyperbola equation for a horizontal transverse axis (that's math-speak for opening left and right):

(x²/a²) - (y²/b²) = 1
Substitute our values for 'a' and 'b':
(x²/3²) - (y²/2²) = 1

And simplified, that gives us:
(x²/9) - (y²/4) = 1
There you have it! That's the secret handshake, the mathematical DNA, the equation for the hyperbola shown in the graph. It's a beautiful, concise way to describe those dramatic, swooshing curves. It tells us where it's centered, how wide its arms are (that's 'a'), and how far apart its asymptotes are, which is dictated by 'b'.
Think of it this way: if the hyperbola were a celebrity, 'a' would be its height and 'b' would be its charisma – both contributing to its overall public image. And the equation is its biography. Pretty neat, huh? So next time you see a hyperbola, don't run screaming. Give it a friendly nod, knowing you've unlocked its mathematical secrets.
