Write A Sequence Of Transformations That Maps Quadrilateral Abcd

Hey there, design enthusiasts and geometric gurus! Ever look at a perfectly formed shape and think, "Wow, that's art!"? Well, guess what? Mathematics is practically the ultimate art form, and today, we're diving into a fun, accessible way to manipulate shapes – specifically, quadrilaterals. Think of it like giving your favorite armchair a makeover, but with math! We're talking about transforming a quadrilateral ABCD, and trust me, it's way more exciting than assembling IKEA furniture.
You know those cool optical illusions that make a flat drawing pop out in 3D? Or how graphic designers can take a simple logo and twist it, stretch it, and rotate it into a hundred different versions for various campaigns? That's the magic of transformations. It’s all about moving, flipping, or resizing shapes without fundamentally changing what they are. It's like a chameleon changing its colors, but for geometry!
So, what exactly are these "transformations" we're chatting about? Imagine you have a physical shape, like a cool cookie cutter. You can slide it across the dough (that's a translation), flip it over to make a mirror image (that's a reflection), spin it around a central point (that's a rotation), or make it bigger or smaller (that's a dilation). These are the foundational moves in our geometric dance.
The ABCD Quadrilateral: Our Canvas
Let's set the stage. We've got our trusty quadrilateral, ABCD. Picture it as a blank canvas, maybe a quirky rooftop patio with distinct corners labeled A, B, C, and D. Or perhaps it's the layout of your dream studio apartment. Whatever it is, it's got four vertices, four sides, and four angles. Our mission, should we choose to accept it, is to move this shape around using a sequence of transformations. It's like giving our patio a complete reno, or rearranging the furniture in our studio to make it feel brand new.
Why ABCD? It's a standard way to name our shape. A, B, C, and D are the corners, and when we connect them in that order, we trace out our quadrilateral. Think of it like following a treasure map – from A, you go to B, then C, then D, and finally back to A to complete the loop.
The Transformation Toolbox: Let's Get Creative!
We've got a few key tools in our transformation belt. Let's break them down:
1. Translation: The Smooth Slide
This is the most straightforward. A translation is simply sliding a shape from one position to another. No spinning, no flipping, just pure, unadulterated movement. Imagine pushing your dining table across the floor – that's a translation. In math terms, we're adding a specific amount to the x-coordinates and another specific amount to the y-coordinates of each point of our quadrilateral.
For example, if point A is at (2, 3), and we want to translate it 4 units to the right and 2 units up, the new A (let's call it A') would be at (2+4, 3+2) = (6, 5). We do this for all four points (B, C, and D) to move the entire quadrilateral. It's like giving your favorite piece of art a new spot on the wall – same artwork, different vibe.
Practical Tip: Think about redecorating a room. You don't change the furniture; you just rearrange it to create a new flow and feel. Translation is your geometric furniture mover!
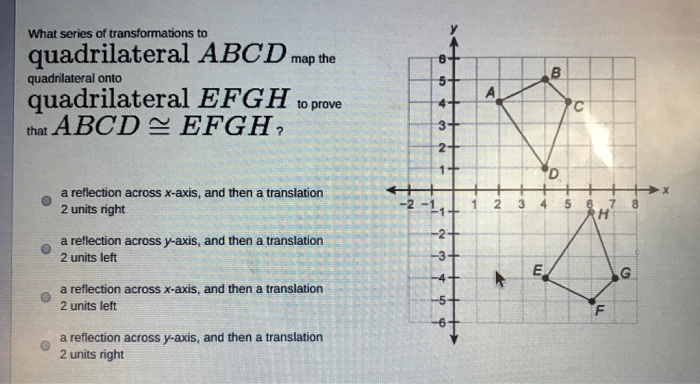
2. Reflection: The Mirror Image Magic
Reflections are like looking in a mirror. You get a flipped version of your shape. The original shape and its reflection are congruent, meaning they are exactly the same size and shape, just oriented differently. We can reflect across the x-axis, the y-axis, or even a diagonal line. It's like seeing your reflection in a calm lake – the image is there, but it's reversed.
If we reflect point A (x, y) across the x-axis, the new A' becomes (x, -y). If we reflect across the y-axis, A' becomes (-x, y). It’s a simple flip, but it can drastically change how a design is perceived. Think about how some logos have a mirrored version for different applications – it maintains brand recognition while offering visual variety.
Fun Fact: Did you know that palindromes, like "madam" or "racecar," are words that read the same forwards and backward? They're a linguistic form of reflection!
3. Rotation: The Spin Cycle
Rotations are all about spinning a shape around a fixed point, called the center of rotation. You can rotate by 90 degrees, 180 degrees, 270 degrees, or any angle you like! Imagine a carousel at a fair – the horses go around and around the central pole. That's a rotation. It's a fantastic way to add dynamism to a design.
Rotating a point (x, y) 90 degrees counterclockwise around the origin (0,0) gives you a new point (-y, x). A 180-degree rotation gives you (-x, -y), and a 270-degree counterclockwise rotation (or 90 degrees clockwise) gives you (y, -x). This is super useful in animation and graphic design, where you see objects subtly or dramatically turning.
Cultural Reference: Think of the intricate patterns in Islamic art, which often rely heavily on rotational symmetry. It’s a testament to how elegant a simple spin can be.
4. Dilation: The Zoom In/Zoom Out
Dilation is when you resize a shape. You can make it larger (an enlargement) or smaller (a reduction). It's like using the zoom feature on your camera or smartphone. The shape remains similar, meaning its angles stay the same, but its sides are scaled up or down by a certain factor, called the scale factor. If the scale factor is greater than 1, it's an enlargement. If it's between 0 and 1, it's a reduction.

If we dilate point A (x, y) from the origin with a scale factor 'k', the new A' becomes (kx, ky). This is how we get those amazing miniature versions of famous landmarks for souvenirs or how movie posters make the main characters look larger than life.
Entertainment Nugget: Think of those "honey, I shrunk the kids" movies. That's dilation in action, making everything appear huge from the perspective of the shrunken characters!
Crafting a Transformation Sequence for ABCD
Now, the real fun begins: combining these transformations. A sequence of transformations means performing more than one of these moves, one after the other, to get from our original quadrilateral ABCD to a new, transformed quadrilateral A''B''C''D''.
Let's say we want to move our quadrilateral. We can do it in stages. Imagine our ABCD is a quirky, L-shaped building block on a blueprint. We want to move it to a new location, maybe flip it to face a different direction, and perhaps slightly shrink it to fit a smaller space.
Here’s a possible sequence:
Step 1: Translation - Giving it a New Address
First, let's translate ABCD. Let's say we want to move it 5 units to the right and 3 units down. Our original points (A, B, C, D) will become (A', B', C', D') by adding 5 to each x-coordinate and subtracting 3 from each y-coordinate. This moves the entire shape without changing its orientation or size.

For example, if A was at (1, 7), A' would be at (1+5, 7-3) = (6, 4).
Step 2: Rotation - Adding a Little Flair
Now that our quadrilateral is in its new neighborhood, let's give it a spin. Let's rotate A'B'C'D' by 180 degrees around the origin. This will flip it upside down. A point (x, y) becomes (-x, -y). So, A' at (6, 4) would become A'' at (-6, -4).
This is like turning your favourite photo frame to hang it in landscape mode. The image is the same, but its presentation has shifted dramatically.
Step 3: Reflection - Creating a Mirror Image (Optional but Fun!)
To make things a bit more interesting, let’s add a reflection. Let's reflect A''B''C''D'' across the y-axis. A point (x, y) becomes (-x, y). So, A'' at (-6, -4) would become A''' at (-(-6), -4) = (6, -4).
This might sound complicated, but think of it as creating a symmetrical pattern. If you're designing a symmetrical garden, you might reflect one half of your design to create the other. It's a classic design principle.
Step 4: Dilation - Adjusting the Scale
Finally, let's adjust the size. Let's say we want to make our quadrilateral smaller, perhaps by a factor of 0.5 (halving its size). We'll dilate A'''B'''C'''D''' from the origin with a scale factor of 0.5. A point (x, y) becomes (0.5x, 0.5y).
So, A''' at (6, -4) would become A'''' at (0.5 * 6, 0.5 * -4) = (3, -2).
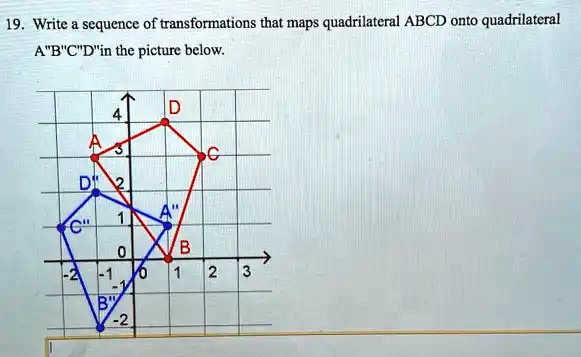
And there you have it! Our original quadrilateral ABCD has gone through a journey of translation, rotation, reflection, and dilation, ending up as A''''B''''C''''D''''. The final shape is related to the original, but it’s in a completely new position, orientation, and size.
Why Does This Matter? Beyond the Math Class
You might be thinking, "Okay, that's neat, but how does this apply to my life?" Well, think about it. Every time you arrange furniture, choose an outfit, or even plan a route on a map, you're unconsciously using principles of transformation.
When you rotate your phone to watch a video, you're performing a rotation. When you zoom in on a photo, that's dilation. When you mirror an image in a photo editor, you're reflecting. These mathematical concepts are woven into the fabric of our visual and spatial experiences.
In graphic design, these transformations are the bread and butter. Creating different versions of a logo for various platforms, animating elements in a website, or designing eye-catching advertisements all rely on these fundamental geometric operations. Even in architecture and urban planning, understanding how shapes can be moved, rotated, and scaled is crucial for creating functional and aesthetically pleasing spaces.
Cultural Insight: Consider the art of origami. It’s all about folding paper, which is a form of transformation (a reflection and a fold creating new shapes). The intricate designs that emerge are a beautiful testament to what can be achieved with simple geometric principles.
A Little Reflection for Your Day
Our quadrilateral ABCD, on its journey through a sequence of transformations, is a bit like us navigating life. We move from one experience to another (translation), we sometimes face new perspectives that flip our understanding (reflection), we adapt and grow in different directions (rotation), and we often scale our ambitions up or down depending on circumstances (dilation).
The beauty is that even after all these changes, the core of who we are, the fundamental shape of our being, remains intact. We are simply experiencing the world from a new vantage point, with a fresh orientation, and perhaps at a different pace. So, the next time you see a shape being manipulated, remember it's not just math; it's a visual metaphor for the dynamic, ever-changing, and ultimately resilient nature of life itself. Embrace the transformations, and see where they take you!
