Write A Polynomial That Satisfies The Given Conditions
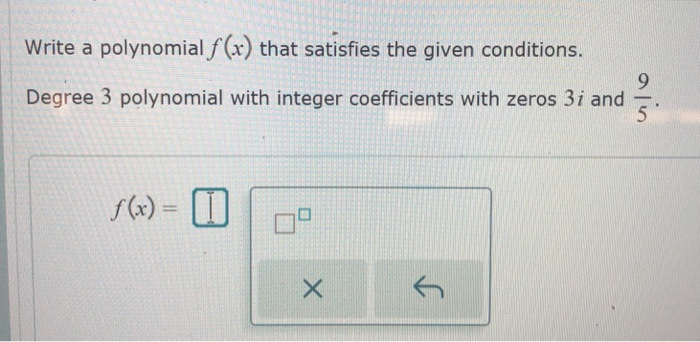
Imagine you're baking a cake, but instead of flour and sugar, you're using numbers and letters! That's kind of what we're doing when we "write a polynomial that satisfies the given conditions." Sounds a bit like a secret agent mission, doesn't it? Except, our spies are numbers and our secret codes are equations.
Let's say you have a bunch of secret desires for your cake. Maybe you want it to be a certain height at a specific time, or perhaps you want it to reach its peak deliciousness exactly when your best friend arrives. These are your "conditions," your desired outcomes. And your polynomial? That's the magical recipe that makes your cake behave exactly as you've envisioned.
Think about it like this: you want to plan a surprise party. You know your friend, let's call her Eleanor, loves ice cream. You also know she absolutely hates broccoli. So, your party conditions are: "Lots of ice cream" and "Zero broccoli." Now, how do you create the perfect party plan? You need to make sure the ice cream supply is always abundant (that's like saying the polynomial should have a specific value) and that no broccoli, not even a tiny speck, makes it onto the dessert table (that's like saying the polynomial should equal zero at a certain point).
Writing a polynomial is like figuring out the secret ingredient list and the exact baking instructions to achieve precisely what you want. Sometimes, the conditions are straightforward. You might want a polynomial that hits the number 5 when you plug in the number 2. Easy peasy. It's like saying, "I want my cake to be exactly 5 inches tall when it's been in the oven for 2 minutes."
But sometimes, the conditions get a little more interesting. You might want your polynomial to be 0 when you plug in 3, and also 0 when you plug in -1. This is like saying, "I want my party to be a complete surprise (zero stress!) when I tell my friend it's on Tuesday (plug in 3), and also zero awkwardness if my cousin brings his weird parrot (plug in -1)."
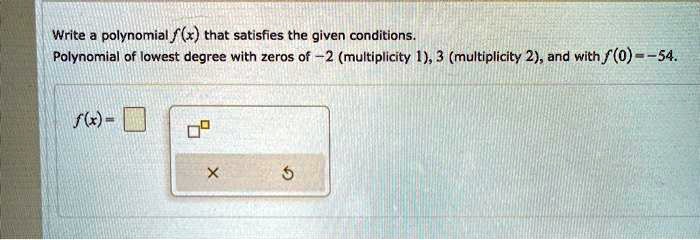
The amazing thing is, there's a whole toolbox of tricks to build these number recipes. We can use what are called "roots." Roots are basically the numbers that make your polynomial equal zero. If you know where your polynomial must be zero, you've already got some of the building blocks. It’s like knowing that if you mention the word "karaoke," your friend Eleanor will immediately start singing (the polynomial hits zero!).
So, if you know your polynomial needs to be zero at 3 and -1, you can start building. You'd put in things like "(x - 3)" and "(x + 1)". These are like the basic spices in your recipe. When you multiply them together, something magical happens. If you put in 3, the (x - 3) part becomes (3 - 3), which is 0. And anything multiplied by 0 is 0! Boom! One condition met.

Then, if you put in -1, the (x + 1) part becomes (-1 + 1), which is also 0. And again, 0 times anything is 0! Another condition satisfied. Your polynomial is starting to look like a successful party planner, ensuring all the important moments are perfectly calibrated.
But what if you have more conditions? Maybe you want your polynomial to be 0 at 3 and -1, but you also want it to be a whopping 12 when you plug in the number 1? This is like saying, "My party is a zero-stress zone for Eleanor and her parrot, and when my Uncle Barry (plug in 1) arrives, I want him to be absolutely blown away by the sheer volume of delicious cheese puffs (the polynomial equals 12)!"

To handle this, we need to add a little more to our recipe. We might need to multiply our existing polynomial by some extra number. This is like adding a pinch of something special to make the flavor even richer. We call this a "leading coefficient." It's the secret multiplier that adjusts the overall "oomph" of your polynomial, ensuring it hits those higher targets.
It's a bit like detective work. You're given clues – these are your conditions – and you have to piece together the puzzle to find the one polynomial that fits all of them. Sometimes the solutions are simple, like a single dash of hot sauce. Other times, they're more complex, like a multi-layered ganache with edible gold leaf. But the beauty is, with the right tools and a little bit of number-crunching creativity, you can always build that perfect polynomial.
And the best part? These polynomials aren't just for abstract math problems. They're used in so many cool things! They help design rollercoasters that give you just the right thrill, they help predict the weather (though sometimes they get it wrong, just like a party guest arriving too early!), and they even help create amazing computer graphics. So, the next time you see a perfectly swooping curve on a screen or feel the perfectly calculated jolt on a ride, remember there might be a cleverly written polynomial working its magic behind the scenes, all thanks to a set of carefully crafted conditions.
