Which Statement Is True About Kinetic Molecular Theory

Remember that time you were at a ridiculously crowded concert? The air was thick, everyone was practically on top of each other, and if someone coughed even slightly, you were guaranteed to get a face full of… well, let’s not dwell on that. It felt like the whole universe was just a giant, buzzing, vibrating blob of people. Well, funny thing, that feeling you had? It's actually a surprisingly accurate, albeit slightly exaggerated, picture of what’s going on at a molecular level. Pretty neat, huh?
My little concert flashback is my way of diving headfirst into the wonderfully weird world of the Kinetic Molecular Theory (KMT). It’s this super-important set of ideas that helps us understand why stuff behaves the way it does, especially gases. Think of it as the superhero origin story for why your soda fizzes or why a balloon pops if you leave it in the sun. You might be thinking, "Kinetic what-now?" Stick with me, it's not as scary as it sounds. It's all about tiny things moving around, and honestly, isn't that the basis of most things in life? Just a bunch of stuff jiggling andiggling?
So, What's the Big Deal with KMT?
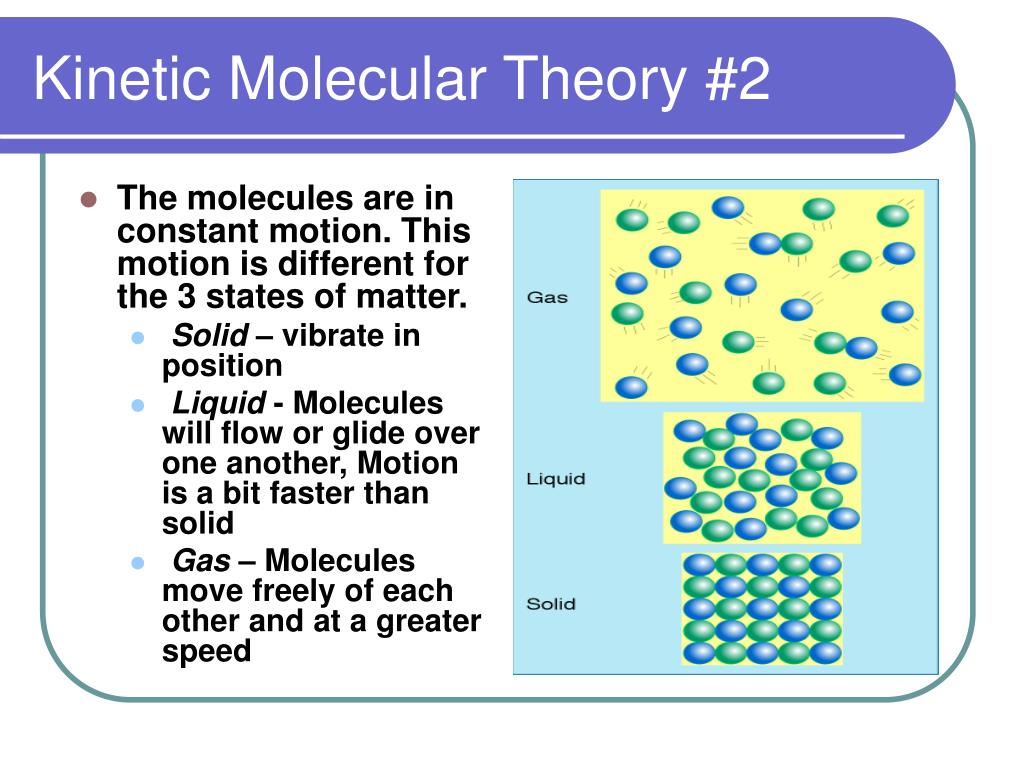
Essentially, the Kinetic Molecular Theory is a model. It's not like, the actual molecules themselves, but it’s our best guess, based on tons of observations and experiments, to describe how these minuscule particles (atoms, molecules, ions – the tiny building blocks of everything) behave. And when we talk about KMT, we're usually focusing on gases. Why gases? Because they’re the wildest dancers in the molecular ballroom. Solids are like polite waltzers, liquids are a bit more of a shuffle, but gases? They're doing the cha-cha, the tango, and maybe a little bit of interpretive dance all at once.
The KMT makes a few key assumptions. These are the bedrock, the commandments, if you will, of molecular movement. If you can wrap your head around these, you’re golden. Let’s break them down, shall we? No pop quiz at the end, I promise.
Assumption 1: Molecules Are TINY and FAR Apart
Okay, so the first biggie is that gas particles themselves are considered to be negligible in volume. What does that even mean? It means compared to the total space they occupy, the actual physical size of the individual molecules is so incredibly small that we can practically ignore it. Imagine a few marbles scattered in a huge gymnasium. The marbles themselves take up hardly any space compared to the vastness of the gym. That’s the idea.
This also means there's a huge amount of empty space between gas particles. They're not huddled together like they were at that concert, trying to catch a glimpse of the stage. Nope, they’re zipping around in this expansive emptiness. This is why gases are so compressible, right? You can squish them because there’s all that room to play with. Unlike, say, trying to squeeze a brick. Good luck with that.
Assumption 2: They Never, Ever Stop Moving
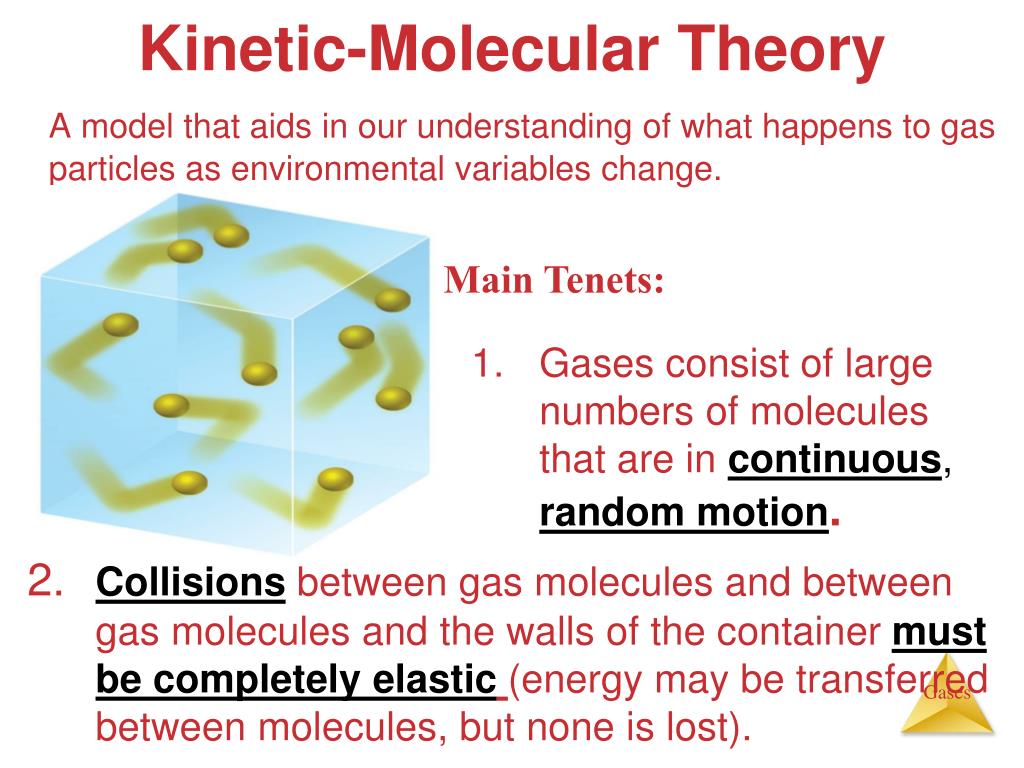
This is where the "kinetic" part comes in. Kinetic means related to motion. And in KMT, gas particles are in constant, random motion. They’re not just chilling; they're perpetually on the go. Think of a bunch of hyperactive toddlers let loose in a candy store. They're bumping into walls, bouncing off each other, changing direction seemingly without rhyme or reason. That’s our gas molecules!

This random motion is crucial. It’s not like they’re all marching in a parade. They’re moving in straight lines until they collide with something – another particle or the walls of their container. Then, boing, they change direction and keep on trucking. It’s this ceaseless, chaotic dance that gives gases their unique properties. It's like the ultimate game of molecular pinball.
Assumption 3: Collisions? Totally Elastic!
Now, this is a bit of a theoretical simplification, but it’s a really important one. The KMT states that all collisions between gas particles, and between particles and the container walls, are perfectly elastic. What’s an elastic collision? Think of a super bouncy ball. When it hits a surface, it bounces back with almost the same amount of energy it had before. No energy is lost as heat or deformation.
In the real world, no collision is perfectly elastic. Some energy is always lost. But for gases, especially ideal gases (which KMT often describes), we assume this energy loss is negligible. This is key because if energy were lost with every collision, the particles would eventually slow down and stop moving. And then, well, no more gas! It's like the universe has a magic rulebook that says, "Nope, you gotta keep moving, kids."
Assumption 4: They Don't Really Care About Each Other
This one is a bit counterintuitive, but stick with it. The KMT assumes that there are no significant attractive or repulsive forces between gas particles. They're basically loners. They might bump into each other, but they don't "like" or "dislike" each other. They don't stick together or push each other away when they're not colliding.
Again, this is an idealization. Real molecules do have intermolecular forces. Think about how water molecules like to huddle together to form liquid water. But for gases, especially at low pressures and high temperatures, these forces are very weak compared to the energy of motion the particles have. So, in essence, they’re just passing by each other like strangers on the street, totally unbothered.
Assumption 5: Temperature is Key to Motion!
And finally, the grand finale: the average kinetic energy of gas particles is directly proportional to the absolute temperature of the gas. This is a mouthful, so let’s unpack it. Absolute temperature, by the way, means temperature measured on a scale like Kelvin, where zero is the theoretical point of no molecular motion. So, basically, hotter gas means faster particles, and colder gas means slower particles.
When you heat a gas, you're literally adding energy to it, and that energy makes the molecules move faster. They zip around with more vigor, hit the walls harder, and generally become more energetic. Conversely, when you cool a gas, you're taking energy away, and the particles slow down. It’s like giving them a molecular lullaby. This is why a balloon expands in the sun (hotter = faster molecules = more outward push) and shrinks in the freezer (colder = slower molecules = less outward push).
Which Statement Is True About Kinetic Molecular Theory? The Big Reveal!
So, given all those assumptions, what kind of statements can we make that are true about the Kinetic Molecular Theory? We’ve already touched on many, but let’s see if we can nail down some solid truths that often appear in questions or discussions about KMT.
Here are some statements that are generally considered true based on the Kinetic Molecular Theory:
- Gas particles are in constant, random motion. (We hammered this one home, remember the hyperactive toddlers?)
- The volume of the gas particles themselves is negligible compared to the total volume of the container. (The marbles in the gymnasium analogy.)
- There are no significant attractive or repulsive forces between gas particles. (The "strangers on the street" idea.)
- Collisions between gas particles and with container walls are perfectly elastic. (The super bouncy ball.)
- The average kinetic energy of gas particles is directly proportional to the absolute temperature of the gas. (Hotter = faster, colder = slower.)
Now, let’s look at some statements that might be presented as true, but are actually false, according to the strict KMT for ideal gases. Understanding these common misconceptions is just as important as knowing the truths.
- Gas particles are stationary until heated. (Nope! Always moving.)
- Gas particles have strong attractive forces. (The opposite is assumed.)
- Collisions between gas particles lose energy. (They are assumed to be elastic, meaning no energy loss.)
- The volume of the gas particles themselves is significant compared to the container volume. (We assume it's negligible.)
- Temperature has no effect on the motion of gas particles. (Big NO. Temperature is a measure of their motion!)
Why Does This Matter?
You might be thinking, "Okay, these are nice theoretical ideas, but what’s the practical application?" Oh, my friend, it’s everywhere! The KMT is the foundation for understanding many gas laws, like Boyle's Law, Charles's Law, and the Ideal Gas Law. These laws help us predict how gases will behave under different conditions, which is crucial for everything from weather forecasting to chemical engineering to even how your car engine works.
It helps explain why blowing up a balloon is possible (all that empty space!), why a hot air balloon rises (heating the air makes it less dense because the particles move faster and push outward more strongly), and why a pressure cooker works (trapping steam increases pressure, making water boil at a higher temperature). It’s like having a secret decoder ring for the physical world!
Think about cooking. When you boil water, you see steam. That’s water molecules escaping their liquid state and becoming a gas. The KMT helps us understand the energetic nature of those steam molecules. Or imagine a can of aerosol spray. The pressure inside is due to those gas molecules constantly colliding with the can's walls. Shake it up? You're just making them bounce around even more energetically, increasing the pressure!

Even something as simple as a scent spreading across a room is explained by KMT. Those perfume molecules are released, and because they're in constant, random motion, they eventually spread out until you can smell them. If they weren't moving randomly, you'd only smell the perfume right where it was sprayed, which would be… anticlimactic.
The "Ideal" vs. "Real" Gas Dance
It’s important to remember that KMT describes an ideal gas. Real gases aren't perfectly ideal. As I mentioned, real molecules do have attractive forces, and their collisions aren't perfectly elastic. However, the KMT is an incredibly useful model because, under many common conditions (like relatively low pressure and high temperature), real gases behave very closely to ideal gases.
When do real gases start to deviate significantly from ideal behavior? Usually, when you try to make them behave like a liquid or a solid. That is, when you increase the pressure (forcing the particles closer together, making their volume less negligible and intermolecular forces more significant) or decrease the temperature (slowing them down, making attractive forces more impactful).
So, when you see a statement about Kinetic Molecular Theory, ask yourself: does it align with these five core assumptions? Is it talking about constant, random motion? Negligible volume? Elastic collisions? No intermolecular forces? And the direct link between temperature and kinetic energy? If it hits those points, you're likely looking at a true statement for the KMT of an ideal gas.
It’s all about these tiny, energetic particles doing their thing. And honestly, the more you think about it, the more you realize how much of our world is governed by these fundamental principles. So next time you see steam rising or a balloon inflate, give a little nod to the Kinetic Molecular Theory. It’s the invisible force behind the visible world, and it's pretty darn cool.
