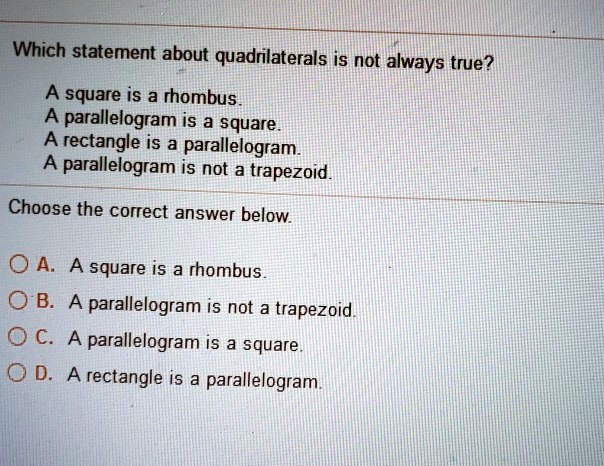
Which Statement Is Not Always True For A Parallelogram
Imagine you're at a picnic, right? You've got your trusty picnic blanket spread out, and you notice its shape. It's probably a rectangle, a nice, neat shape. Now, picture a bunch of those picnic blankets lined up side-by-side, creating a long, winding path. That's kind of like what we're talking about today, but with shapes. We're going to explore the wonderfully wobbly world of shapes that aren't quite as predictable as they seem. Specifically, we're going to have a little fun with something called a parallelogram.
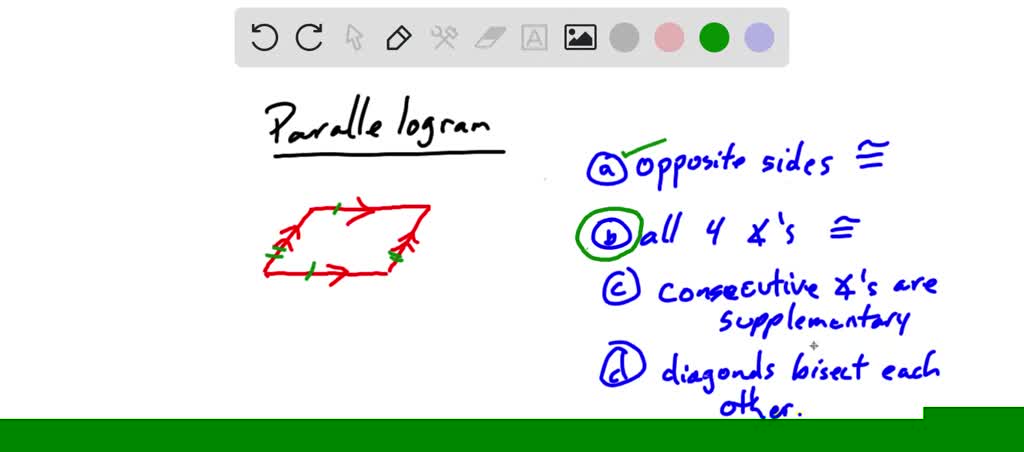
Think of a parallelogram like a friendly, slightly mischievous cousin to a rectangle. It's got four sides, and its opposite sides are like best buddies – they're always the same length and they run perfectly parallel to each other, like train tracks. Pretty cool, right? It’s like they’re always whispering secrets to each other, forever running alongside without ever meeting. And its opposite angles? Also best buddies! They're always the same size. This makes parallelograms feel very balanced and fair, like everyone gets a turn.
Now, we often think of parallelograms as looking like a tilted rectangle, or maybe a leaning tower of shapes. And yes, many of them do! Think of a classic rhombus, with all sides equal – that's a super-duper special parallelogram. Or a square, which is basically a rectangle that decided to be a rhombus too! These are the show-offs of the parallelogram family, always sticking to all the rules with extra enthusiasm.
But here's where things get interesting, and where our little shape exploration takes a surprising turn. While many statements about parallelograms are always true, like those parallel sides and equal opposite angles, there's one little detail that sometimes trips us up. It’s like trying to remember if you turned off the oven – you usually do, but sometimes, just sometimes, you might forget.
Let's talk about the sides. We know opposite sides are always equal. That’s like knowing your mom and dad will always be there for you. Then there are the angles. Opposite angles are always the same size. That's like having two best friends who are both really good at telling jokes – they’ll always bring the same amount of laughter.
So, what's the statement that isn't always true? It’s about the angles. Specifically, it's about whether all the angles in a parallelogram are the same. Think about a rectangle. All its corners are perfect, crisp 90-degree angles. They’re like little squares, very polite and precise. Because a rectangle is a type of parallelogram, you might think, "Aha! All parallelograms have perfect 90-degree angles!" But that's where our mischievous parallelogram likes to play a little trick.
Imagine you’re pushing on the sides of a cardboard box. If you push just right, the perfectly square corners can start to lean. They become those lovely, slanted angles we see in a typical parallelogram. The opposite corners might still be equal, and the opposite sides are still running parallel, but those angles? They're not 90 degrees anymore! One pair of opposite angles might be sharp and pointy (less than 90 degrees), and the other pair might be wide and gaping (more than 90 degrees). They’re like a happy, wobbly dance.
It's like the difference between a perfectly made bed and one that’s been slept in all cozy and a little rumpled. Both are beds, both are comfortable in their own way, but their exact shapes can vary!
So, the statement "all angles in a parallelogram are 90 degrees" is not always true. While it can be true (when the parallelogram is also a rectangle or a square, the superstars!), it doesn't have to be. This is what makes parallelograms so fascinating. They're flexible, adaptable, and can take on so many different forms, all while keeping their core parallelogram identity. They’re the shape equivalent of a chameleon, able to blend into different moods and situations.

Think about it this way: If someone says, "All dogs bark," is that always true? Well, mostly! But what about Basenjis? They don't bark in the traditional sense; they yodel! Similarly, while most parallelograms have those beautifully slanted angles, the ones that are perfectly rectangular have those special 90-degree angles. So, you can't make a blanket statement about all the angles being the same size.
It's a gentle reminder that not everything in life has to be rigidly perfect to be wonderful. Parallelograms show us that there's beauty in variation, and that even when things lean a bit, they can still be strong, structured, and incredibly useful. From the way buildings are designed to the patterns we see in nature, these friendly, sometimes wobbly shapes are everywhere, reminding us to appreciate the slightly imperfect, wonderfully diverse world around us. They’re the unsung heroes of geometry, quietly holding things together with their reliable parallel sides and their charmingly varied angles.
