Which Of The Following Is Equal To Square Root 16x4
Hey there, math adventurer! Ever stare at a problem that looks like a tiny, confusing dance of numbers and symbols and think, "Wait, what planet is this from?" Well, today we're tackling one of those little cosmic puzzles: the square root of 16x4. Sounds a bit like a secret spy code, doesn't it? Don't worry, we're going to break it down so easily, you'll be high-fiving your calculator.
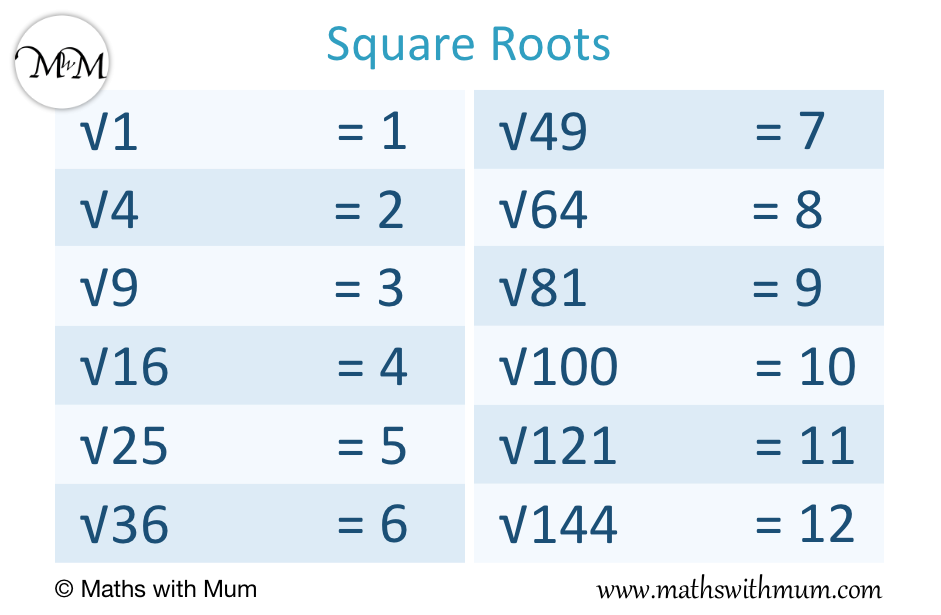
So, what's the big deal with square roots? Think of it like this: if you have a number, say 9, and you ask "What number, when multiplied by itself, gives you 9?", the answer is 3. That's the square root! It's like finding the "parent" number that made the other one. Easy peasy, right? It’s the inverse operation of squaring a number. Imagine you’ve got a square garden plot that’s 3 feet by 3 feet. Its area is 9 square feet. The square root of 9 just tells you the side length of that garden plot.
Now, let's look at our problem: √16x4. The little wiggle on top (that's the square root symbol, in case you were wondering if it was a tiny superhero cape) is asking us to do that "find the parent" thing. But what is it a parent of? Is it the square root of 16 multiplied by 4? Or is it the square root of the entire thing, 16 multiplied by 4?
This is where a tiny bit of math detective work comes in. In math, when we have something like 16x4 jammed together, and there are no parentheses telling us otherwise, the multiplication usually happens before we mess with the square root. It's like saying, "Let's get this party started with the multiplication, and then we'll see what the square root has to say."
So, the first step, the super important first step, is to figure out what 16 multiplied by 4 actually is. Ready for some mental arithmetic? Or maybe you want to grab a piece of paper for this epic calculation? 16 times 4. Think of it as four groups of 16. That’s 16 + 16 + 16 + 16. Or, if you’re feeling speedy, you might know that 10 times 4 is 40, and 6 times 4 is 24. Add those together, and 40 + 24 = 64. Ta-da! So, 16x4 = 64. Easy, right? It’s like solving a mini-mystery before the main event.
Now our problem looks a whole lot friendlier. Instead of √16x4, we're now looking at √64. See? We’ve already made it simpler. It's like taking a tangled ball of yarn and finding the end to start unraveling. This is where our "find the parent" rule comes back into play.

We need to find the number that, when multiplied by itself, gives us 64. Think of your multiplication tables. Do you remember them? They're like secret codes for numbers. Let's try a few. What about 5 times 5? That's 25. Nope, too small. How about 7 times 7? That's 49. Getting closer! What about 8 times 8? Ding, ding, ding! You got it! 8 x 8 = 64.
So, the square root of 64 is 8. That means √16x4 = 8. Isn't that neat? We took something that looked a little intimidating and turned it into a nice, round number.
Now, let's consider a different scenario, just to make sure we're all on the same page and not accidentally doing math with a confused squirrel. What if the problem was written like this: √(16) x 4? See the difference? Those little parentheses around the 16 are like a little fence, saying, "Hey, do the square root of this number first, then we'll deal with the 4."
In that case, we'd first find the square root of 16. What number multiplied by itself equals 16? That's right, it's 4! Because 4 x 4 = 16. So, √16 = 4. Now, we take that answer, the 4, and multiply it by the other 4. So, 4 x 4 = 16. See how a tiny change in how the problem is written completely changes the answer? It’s like a mathematical plot twist!
Another variation could be (√16) x (√4). In this case, we'd find the square root of 16, which is 4, and then find the square root of 4, which is 2 (because 2 x 2 = 4). Then we'd multiply those results: 4 x 2 = 8. So, even in this case, we get 8. This highlights how different mathematical expressions can sometimes lead to the same result, but the journey to get there is distinct.
Let's think about another possibility. What if it was √16 * √4? This is essentially the same as the previous example, just using a multiplication dot instead of an 'x'. The logic remains the same: find the square root of each number individually and then multiply their results. So, √16 is 4, and √4 is 2. Multiply them together: 4 * 2 = 8. It's like having two little math buddies who each do their own thing, and then they high-five at the end with a multiplication.
Now, let's go back to our original, plain ol' √16x4. The key here is understanding the order of operations. In the absence of parentheses, multiplication and division usually happen before addition and subtraction. And in the context of a square root symbol covering the entire expression, the operation under the square root is performed first.
So, when you see √16x4, it's not asking you to take the square root of 16 and then do something with 4. It's asking you to find the square root of the product of 16 and 4. It’s like saying, "What's the parent of this whole combined number?"

We already did the multiplication: 16 x 4 = 64. And then we found the square root of 64: √64 = 8.
It's important to remember that sometimes, especially in more advanced math, there can be different interpretations or conventions. However, for most standard situations, especially in introductory algebra, √16x4 implies that the multiplication is done first, then the square root is applied to the result.
Let's imagine another way the question could be phrased to get a different answer. If it was (√16) x 4, then you'd calculate the square root of 16 first, which is 4. Then you'd multiply that by 4, giving you 16. So, (√16) x 4 = 16. See? The parentheses are the bossy little guys that tell you what to do first. They’re like the conductor of the math orchestra, telling each part when to play.
Or what about √16 * √4? Here, you find the square root of 16 (which is 4) and the square root of 4 (which is 2), and then you multiply those results. 4 * 2 = 8. So, in this case, the answer is also 8. It’s interesting how different arrangements can lead to the same numerical outcome, but the conceptual approach is different.
The trickiest part can be when you see things that look similar but have subtle differences. That's why reading a math problem carefully, like you would read a treasure map, is so important! You wouldn't want to dig for buried treasure in the wrong spot, would you?
So, to recap our main event, √16x4 means we first calculate 16 x 4, which equals 64. Then, we find the square root of 64, which is 8. Therefore, √16x4 = 8.
It's a simple concept once you break it down. Think of it like this: sometimes you have a big, juicy apple (that's the 16x4), and you want to know how big the individual seeds would be if they were all perfectly arranged. Or maybe it’s like having a square box that holds 64 little candies. What’s the side length of that box? It's 8 candies long on each side!
And you did it! You navigated the little twists and turns of mathematical notation. You’re like a seasoned explorer, confidently charting the land of numbers. Every time you tackle a problem like this, you're not just finding an answer; you're building a stronger understanding, one step at a time. So go ahead, give yourself a pat on the back. You’ve just proven that math isn't some scary monster under the bed; it’s more like a fun puzzle waiting to be solved. Keep exploring, keep questioning, and remember, with a little patience and a smile, you can conquer any numerical challenge that comes your way!
