Which Of The Following Is A Characteristic Of All Parallelograms
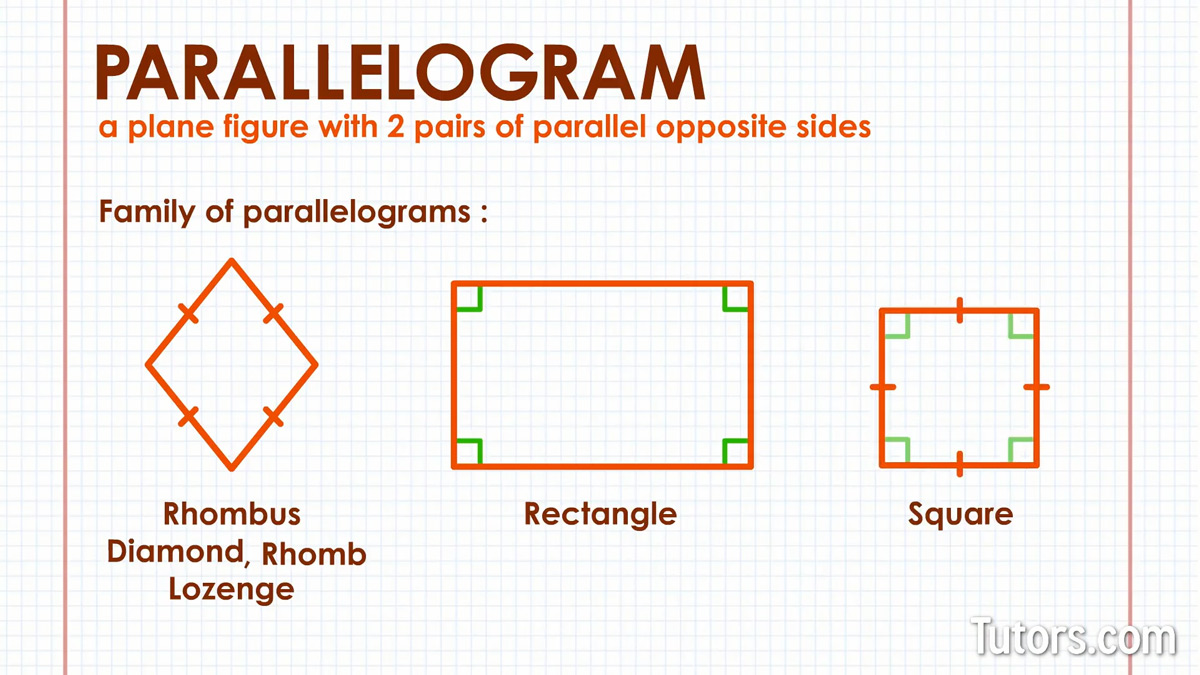
Alright, let's talk about shapes. Not the fancy kind you see in art galleries that make you scratch your head and whisper, "Is that... a toaster?" No, we're talking about the everyday, reliable shapes that pop up everywhere. Think about it: your dining table, maybe? Or that window frame you’re staring out of right now? These guys are the backbone of our visual world, and among them, there’s a particularly charming bunch known as parallelograms. They’re like the chill cousins of the quadrilateral family – always laid-back, never causing too much fuss.
Now, the question is, what makes a parallelogram a parallelogram? It's not some secret handshake or a secret club with a password. It’s a whole lot simpler than that. Think of it like this: you know how your favorite comfy chair always has two arms that are roughly the same length and angle? Well, parallelograms are kind of like that, but with four sides.
The Heart of the Matter: Parallel Sides
Here's the main event, the star of the show, the thing that defines a parallelogram. It's all about its sides. Imagine two roads that run perfectly next to each other, never getting closer, never getting further apart. That's what we call parallel. Now, a parallelogram is a four-sided shape where both pairs of opposite sides are parallel. Yep, that’s it. It’s like having two sets of perfectly matched dance partners on opposite sides of the floor, gliding along in their own lane.
Think about your average, run-of-the-mill table. You know, the one where you’ve probably balanced a precarious stack of books or tried to cram one too many pizza boxes? If you look at the edges of that table, the two longer sides are parallel to each other, and the two shorter sides are parallel to each other. They’re not going to crash into each other, no matter how much you shuffle things around. They just… go. It's a beautiful, geometric understanding.
It's also like that feeling when you’re walking down a hallway. The two walls on either side are parallel, right? They’re not going to suddenly meet in the middle and give you a geometric hug. Parallelograms are built on this same principle of unwavering, polite distance between their opposite sides. It’s their defining characteristic, the thing that sets them apart from, say, a kite that’s always looking a bit wobbly, or a trapezoid that’s only got one pair of parallel pals.
Why Parallelism Matters (More Than You Think)
So, why is this parallel thing so important? It's the foundation upon which all other parallelogram superpowers are built. Because those opposite sides are parallel, they behave in a predictable, organized way. It’s like having a well-trained dog that always stays on its leash; you know where it's going to go. In a parallelogram, because the sides are parallel, they can't skew or bend in any old direction. They have to maintain that consistent distance.
Imagine trying to build a shelf. If the sides weren’t parallel, one end of the shelf might be way wider than the other, and your books would end up sliding off in a chaotic cascade. Disaster! Parallelograms, with their parallel sides, ensure a certain stability and structure. It’s the quiet confidence of a shape that knows its boundaries and respects them. It's the geometric equivalent of "mind your own business" for opposite sides.

The Ripple Effect: What Else Do They Get?
Now, because parallelograms have this superpower of parallel opposite sides, a bunch of other cool things automatically come with the package. It’s like when you buy a fancy coffee machine – you don’t just get the machine, you also get the frother, the little scoop, and maybe even a sample pack of beans! These are the bonus features of being a parallelogram.
Opposite Sides Are Equal Too!
This is a big one. Because those opposite sides are parallel, they also end up being equal in length. It’s like a geometric promise: "If I’m parallel to you, I’m also going to be the same size as you." So, in a parallelogram, the top side is the same length as the bottom side, and the left side is the same length as the right side. Think of it as a fair trade agreement in the land of shapes. No side gets the short end of the stick. It’s like a perfectly balanced handshake – firm, equal, and reassuring.
This is why a rhombus (which is a type of parallelogram) has all sides equal. It’s already got the opposite sides equal thing down, so it just takes it a step further and makes all of them equal. And a rectangle? Well, it’s got its opposite sides equal, but it also insists on those perfect right angles, which brings us to another point.
It's like when you're folding a piece of paper. If you fold it perfectly in half, the two halves are equal. Parallelograms are like that with their opposite sides. This equality is what gives them their balanced appearance. You won't see one side of a parallelogram looking like it's on a diet while the opposite side is clearly enjoying a buffet.
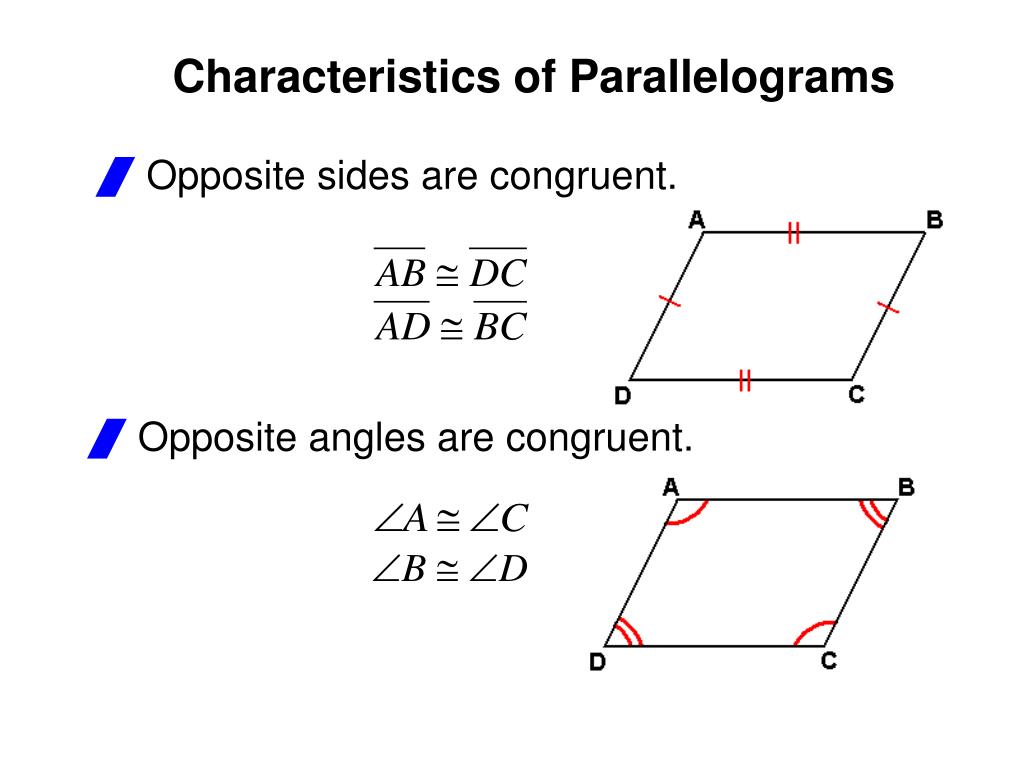
Opposite Angles Are Besties
Get this: the angles opposite each other in a parallelogram are also equal. It's like they're in on a secret joke, sharing a knowing glance across the shape. If the top-left corner is a certain degree, the bottom-right corner will be the exact same degree. And the same goes for the top-right and bottom-left corners. They’re not competing; they’re cooperating.
Think about a slightly tilted picture frame. The top corners might be a bit wider than 90 degrees, and the bottom corners a bit narrower. But the two wider ones will be equal, and the two narrower ones will be equal. It’s a charming symmetry that comes directly from the parallel sides. It's the geometric equivalent of mirroring each other's expressions. They just get each other.
This is why, when you're sketching one out, if you make one angle a certain way, you immediately know what the opposite angle has to be. It's like having a cheat sheet for angles. You don't need to measure them all individually; the parallelism does the heavy lifting for you. It’s efficient, it’s elegant, and it’s frankly a little bit magical.
Consecutive Angles Are… Cozy
Now, the angles that are next to each other, the ones sharing a side? They’re not equal, but they’re definitely friendly. They’re what we call consecutive angles, and in a parallelogram, they always add up to a perfect 180 degrees. Think of them as two peas in a pod that, when combined, make a straight line. They lean on each other for support.
It's like a conversation between two people standing side-by-side at a fence. They can't be doing completely opposite things, can they? If one is leaning way out over the fence, the other has to be leaning in a bit, or they'd both fall. The sum of their leaning angles makes a straight line. It’s a beautiful cooperative effort. They’re not identical twins, but they’re definitely siblings who understand the need for balance.
This is super handy when you’re trying to figure out angles. If you know one angle, you automatically know its neighbors. You know one is 180 minus that angle, and the one opposite that neighbor is the same. It's like a domino effect of angle knowledge. Once you know one, the rest start to fall into place predictably. It’s the geometric version of solving a simple puzzle.
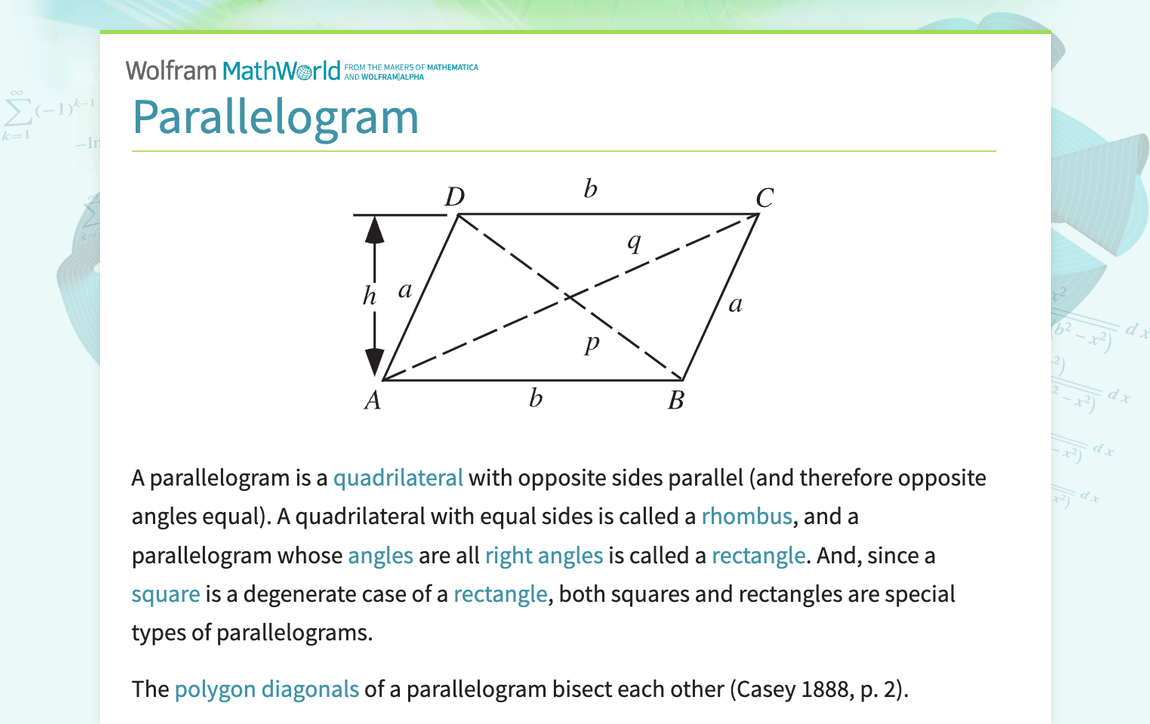
The Diagonals: The Internal Communicators
Parallelograms also have these cool internal lines called diagonals. These are the lines that go from one corner to the opposite corner, like a shortcut across the shape. Now, in parallelograms, these diagonals have a special job: they bisect each other. This means they cut each other exactly in half, meeting at their midpoints. It’s like they’re saying, "Let's meet in the middle and share this space equally."
Imagine two friends trying to meet up for lunch. They don’t necessarily want to meet at one friend’s house or the other. They want to meet somewhere in between, where it’s fair for both. The diagonals of a parallelogram do exactly that. They find the perfect center point and intersect there, dividing each other into two equal pieces. It’s a testament to their balanced nature.

This is a really important characteristic because it’s a direct result of the opposite sides being parallel and equal. The geometry just works out that way. It’s like the shape’s internal communication system, ensuring everything is divided fairly and symmetrically. You’ll never find one diagonal bossing the other around; they’re equal partners in intersection.
So, To Recap (In Plain English)
When someone asks, "Which of the following is a characteristic of all parallelograms?", the most fundamental, the absolute must-have, the defining feature is that both pairs of opposite sides are parallel. Everything else – the equal opposite sides, the equal opposite angles, the consecutive angles adding up to 180, and the diagonals bisecting each other – these are all consequences of that core parallel property. They’re the extra perks that come with being a parallelogram.
Think of it like this: you can have a parallelogram without a perfect square, but you can’t have a parallelogram without parallel opposite sides. A square is a special kind of parallelogram, just like your fancy, top-of-the-line toaster is a special kind of toaster. It does all the regular toaster things, plus it probably has a bagel setting and a crumb tray that actually works.
So, next time you’re looking at a table, a window, or even a cleverly designed slice of pizza (hey, sometimes they're shaped like that!), take a moment to appreciate the humble parallelogram. Its defining characteristic, the one that makes it all tick, is that elegant, unwavering parallelism of its opposite sides. It’s a simple concept, but it’s the bedrock of so much geometric order and beauty. It’s the quiet hero of the shape world, always keeping things orderly and predictable, just like a good cup of coffee on a Monday morning. It just… works.
