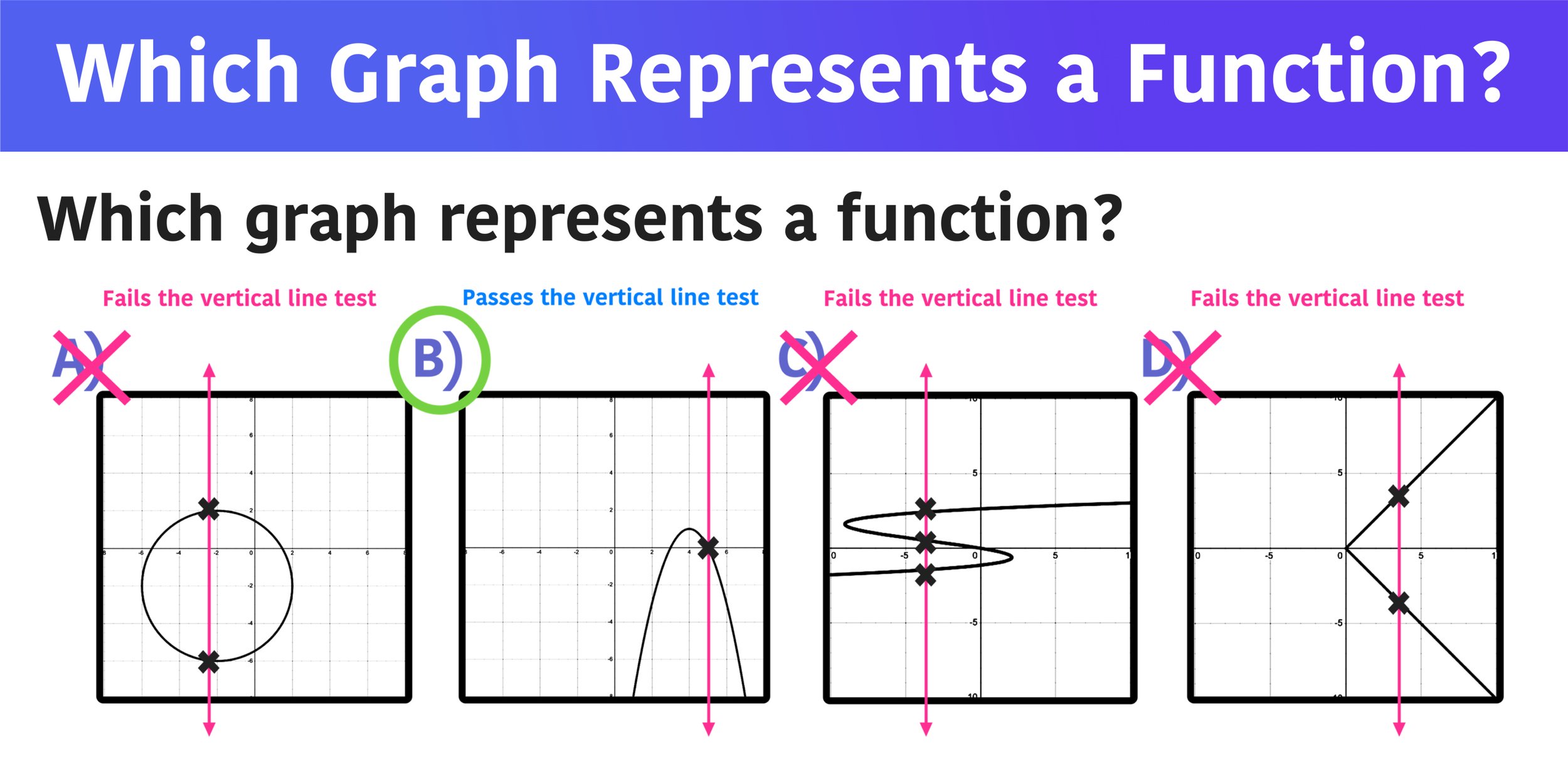
Which Of The Following Graphs Represents A Function
Let's be honest, math can sometimes feel like a secret language. We've all been there, staring at scribbles on a page, wondering if they hold any meaning at all. Today, we're tackling a topic that might sound a little intimidating: functions. But don't worry, we're going to make this as painless, and dare I say, enjoyable, as possible.
Think of it like this: some things in life are super straightforward. You put on your socks, then your shoes. There's a clear order, a definite outcome. It's like a perfectly behaved little machine.
Other things? Well, they're a bit more chaotic. You might try to make toast, and sometimes you get a perfect golden slice, and other times it's practically charcoal. Your toaster is having an off day, or maybe it's just feeling fancy.
The Mystery of the Magical Machine
In the land of graphs, we're looking for those perfectly behaved little machines. These are our functions. They're the reliable ones, the ones you can count on to give you the same answer every time you ask them a question.
Imagine you have a vending machine. You press button 'A1', and you always get a bag of salty crisps. That's a function! No surprises, just pure, unadulterated crisp satisfaction.
But what if you press 'A1' and sometimes you get crisps, but other times you get a fizzy drink? Or worse, a rogue bouncy ball? That vending machine is definitely not a function. It's more of a whimsical mystery box.
Unmasking the Suspects
Now, we're presented with a lineup of graphs. They're all drawn out, looking innocent enough. Our mission, should we choose to accept it, is to figure out which ones are the true functions.

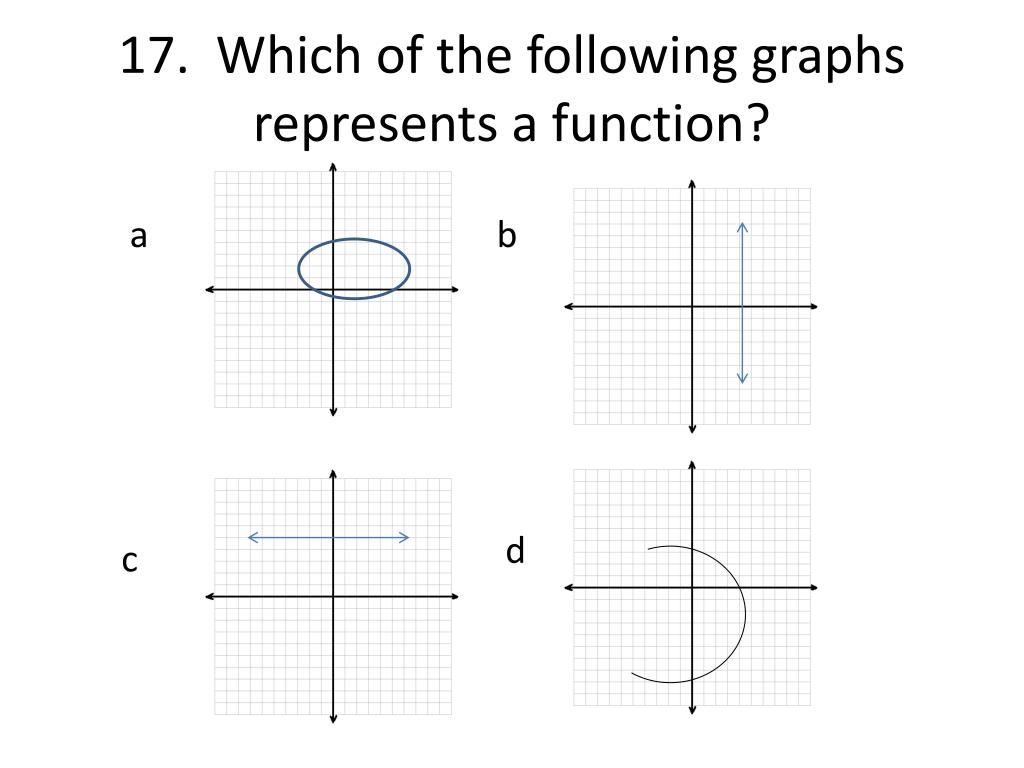
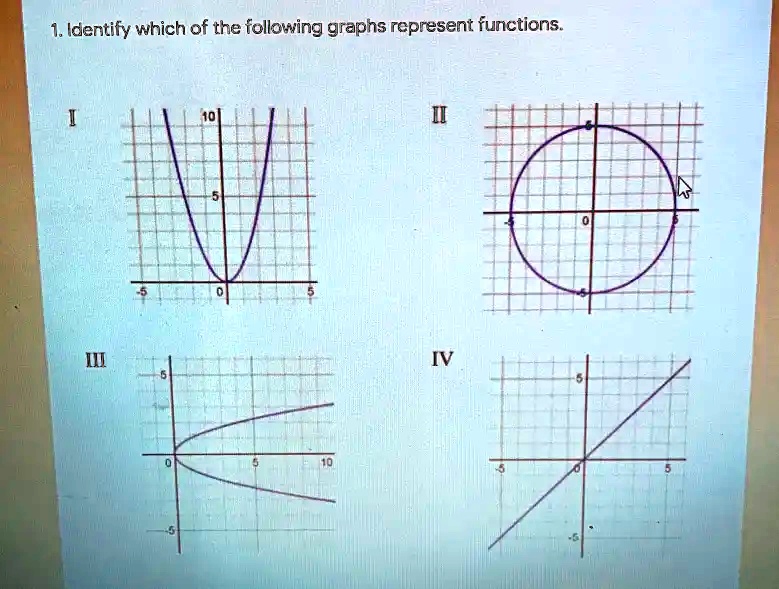
The easiest way to spot a function is to imagine drawing a straight line from top to bottom across the graph. We call this the vertical line test. It’s like shining a flashlight from the side.
If your flashlight beam (the vertical line) only ever hits the graph once, then congratulations, you've found a function! It's behaving itself, giving only one output for each input.
It's like a polite handshake. One hand meets another, and that's it. No awkward double-handshakes here.
But if your flashlight beam hits the graph more than once as you slide it across, then we have a problem. That graph is being a bit of a rebel. It's trying to give multiple answers for the same question.
Think of it like asking your friend, "What did you eat for lunch?" If they say, "I had a sandwich," that's a function. If they say, "I had a sandwich, and also a salad, and maybe some soup," well, that's a bit of a jumble, isn't it?
The Usual Suspects: Common Graph Shapes
Let's look at some common shapes. We have the lovely, smooth parabolas. You know, the ones that look like a happy 'U' or a sad upside-down 'U'.
If a parabola opens straight up or straight down, it usually passes the vertical line test with flying colors. It's the epitome of well-behaved. "Yes, this x-value gives me this y-value, and only this y-value." So dependable.
But if a parabola decides to lie on its side, looking more like a sideways smile, then it's probably not a function. Our flashlight beam will hit it in two places. That's a bit like asking your friend for the time, and they give you two different times. Utterly confusing!
Then we have those straight lines. The ones that go perfectly horizontal or perfectly vertical. A horizontal line? Totally a function. One y-value for all the x's. Simple, elegant, and predictable.
A vertical line, however, is the arch-nemesis of functions. It's like asking a question and getting an infinite number of answers all at once. Every single y-value is associated with that one x-value. It's graph anarchy!
It's the mathematical equivalent of trying to pet a cat and it suddenly sprouting ten extra tails. You're just not sure where to focus.
When Graphs Get a Little Too "Creative"
Sometimes, graphs look like they’ve been drawn by a toddler with a crayon. They might swirl around, loop back on themselves, or just generally look like they're having a party without inviting the vertical line test.
These are the graphs that love to keep you guessing. They might be beautiful in their chaos, but they’re rarely functions. They’re the free spirits of the graph world, unbound by the strict rules of input-output relationships.
Think of a circle. A perfect circle. If you try the vertical line test on a circle, your flashlight beam will likely hit it twice (except at the very left and right edges). That circle is definitely more interested in being a shape than a function.
It's like a group of friends all trying to wear the same hat. Not ideal for a clear photo, and not ideal for a function. Each input should have its own unique output.

The Unpopular Opinion: Maybe Some Graphs Just Want to Be Wild
Here's my little secret, my unpopular math opinion. While we're all trained to find functions, to appreciate their order and predictability, sometimes I look at a graph that isn't a function and I think, "Good for you!"
Maybe that circle is just embracing its roundness. Maybe that swirling line is just expressing itself artistically. Who are we to impose our strict definition of "functionality" on every single drawing?
It's like telling a dog it can only bark once. Sometimes, a dog just needs to let out a good, long howl. And sometimes, a graph just needs to be a little bit wild.
So, when you're faced with a graph, remember the trusty vertical line test. It’s your best friend for identifying functions. But don't forget to appreciate the creativity and freedom of the graphs that choose a different path. They might not be functions, but they’re definitely interesting.
After all, the world needs both perfectly behaved machines and a little bit of delightful chaos. It's what keeps things interesting, wouldn't you agree?
So, the next time you see a graph, give it the old flashlight test. See if it's a faithful function or a whimsical wonder. Either way, you're learning, and that's always a win.
