Which Inequality Is Graphed On The Coordinate Plane
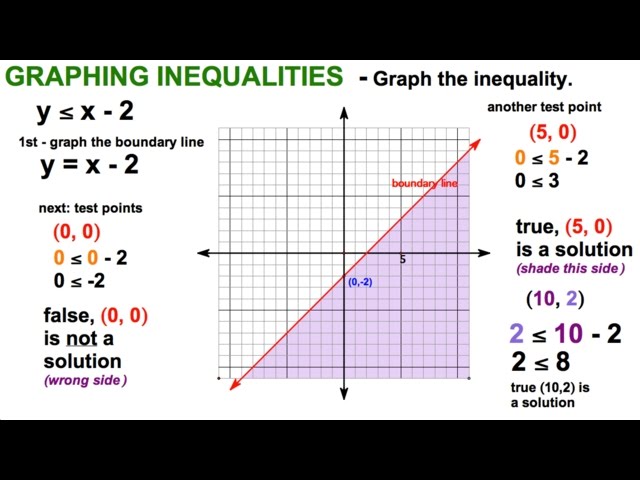
Hey there, math adventurers and graph enthusiasts! Ever find yourself staring at a grid, those trusty x and y axes looking all innocent, and wonder what kind of mathematical mischief is being cooked up there? Well, buckle your seatbelts, because today we're diving headfirst into the wonderfully wild world of inequalities graphed on the coordinate plane! It’s like a treasure map, but instead of buried gold, you're finding entire regions of possibility!
Imagine you're trying to figure out how many cookies you can bake before your mom really starts to give you the "seriously, again?" look. Let's say you have a maximum of 36 cookies you're allowed to make. On a graph, this could be represented by an inequality. If 'x' is the number of chocolate chip cookies and 'y' is the number of oatmeal raisin cookies, and you can't exceed 36 total, you'd have something like x + y ≤ 36. See? That little "less than or equal to" symbol (≤) is your secret decoder ring! It tells you that the total number of cookies you bake must be 36 or less. You're not going to get grounded if you make 30 cookies, but you might have a stern lecture if you decide to bake 40. The graph of this inequality wouldn't be a single point, oh no! It would be a whole area of points, a whole galaxy of cookie combinations that are totally okay! It's like the universe giving you permission to indulge (within reason, of course!).
Now, let's talk about the visual punchline. When you plot an inequality on the coordinate plane, you don't just get a lonely line. Nope! You get a whole shaded region! This shading is the superstar, the main event. It’s like the graph is throwing a party, and the shaded area is where all the fun is happening. Everything inside that shaded area? It's a solution! It's a valid combination, a happy outcome, a "yes, this works!" moment. It’s like saying, "You can have any of these combinations of cookies, and you'll be in the clear!" This is so much cooler than just getting a single number answer, right? It's like getting a whole buffet of correct answers!
Think about another scenario. You're at a restaurant and you've got a strict budget of $50. The fancy steak costs $25 and the delicious pasta is $15. Let 's' be the number of steaks and 'p' be the number of pastas you order. Your inequality might look something like 25s + 15p ≤ 50. Now, you can't exactly order 2.3 steaks, so we're dealing with whole numbers here. But the principle is the same! The graph of this inequality would show you all the possible combinations of steaks and pastas you could order without breaking the bank. You could order 2 steaks and 0 pastas (that's $50, right on the edge of your budget!). You could order 0 steaks and 3 pastas (that's $45, well within your budget). You could even order 1 steak and 1 pasta ($40, a delicious compromise!). The shaded region on the graph would visually confirm all these budget-friendly choices. It's like having a personal financial advisor, but way more colorful and less likely to wear a stuffy suit.
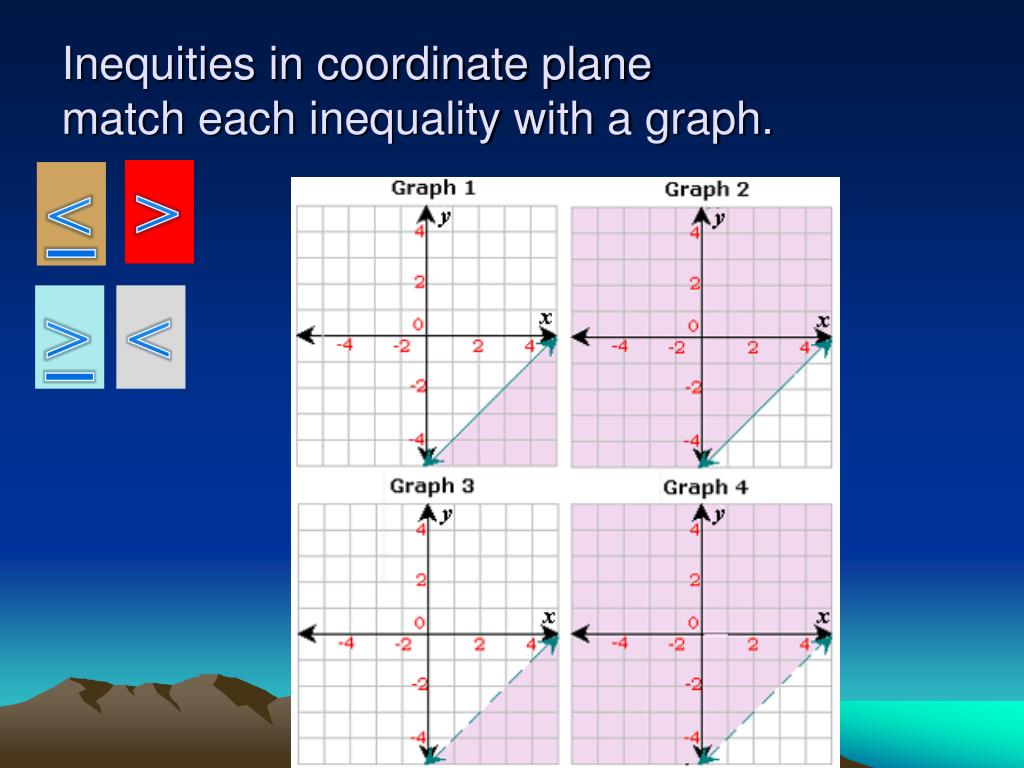
And what about those fancy lines? Sometimes the line itself is solid, and sometimes it’s dashed. This is where the real drama unfolds! If you see a solid line, it means the numbers on the line are also part of the solution. In our cookie example with x + y ≤ 36, if you made exactly 36 cookies (say, 18 chocolate chip and 18 oatmeal), that would fall right on the line, and it's perfectly acceptable. It’s like getting the "yes, and..." of mathematical solutions. If the line is dashed, however, it’s a different story. It’s like a "no-go zone" that you can get really close to, but you can't actually touch. Imagine you have a speed limit of 60 mph. Your inequality might be speed < 60. You can go 59.9 mph, and you're golden. But 60 mph? Nope! That's where the dashed line comes in, saying, "Almost there, but not quite!" It’s the mathematical equivalent of a tantalizing "almost"!
So, the next time you see a graph with a shaded region, don't just see lines and shading. See a world of possibilities! See all the ways things can work out! Whether it’s about cookies, budgets, or speed limits, these inequalities are just fun, visual ways of saying, "Here are all the amazing combinations that fit the bill!" They’re not just abstract math; they’re your permission slips to a world of valid solutions. Isn't that just wonderfully cool?

So, what inequality is being graphed? It's the one that says, "You've got a whole bunch of awesome choices!" It's the inequality that opens up a universe of possibilities on your trusty coordinate plane, painted with the glorious colors of the shaded solution set. It’s the inequality that whispers, "Go forth and be mathematically fabulous!"
It’s about understanding the boundaries, sure, but more importantly, it’s about celebrating the vast, exciting space within those boundaries. It’s the mathematical equivalent of looking at a buffet and saying, "I can have any of these delicious dishes (within my budget, of course!)" It’s a celebration of choice, a visualization of freedom, and a super fun way to see how numbers and regions dance together on the coordinate plane. So, embrace the shading, love the lines (solid or dashed!), and get ready to explore the incredible world of graphed inequalities!
