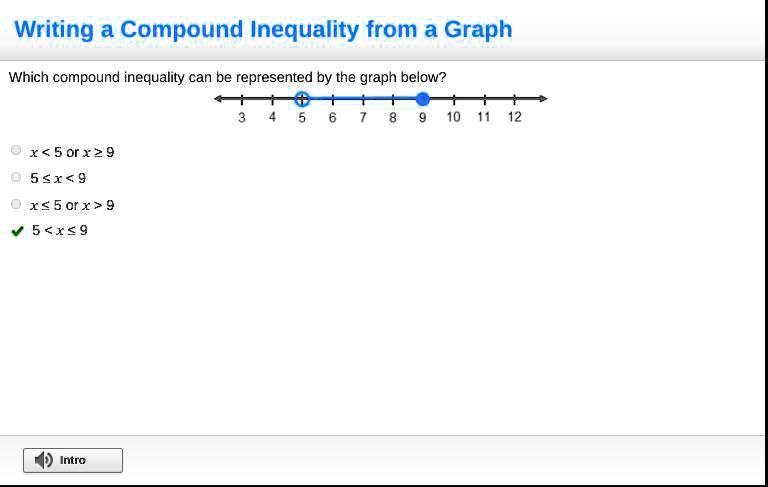
Which Compound Inequality Can Be Represented By The Graph Below
Ever looked at a picture, a map, or even a simple drawing and wondered what it all means? Well, sometimes, those pictures are actually representing mathematical ideas! Today, we're going to dive into a super-fun way math shows up in the world around us: compound inequalities. Think of them as clues that tell us a whole range of numbers are involved, not just one specific spot. It's like saying "I'll be there sometime between 2 PM and 4 PM," instead of a precise 3:15 PM. Pretty neat, right?
Understanding what a graph of a compound inequality represents is incredibly useful, no matter your background. For beginners, it's a fantastic visual aid to grasp abstract mathematical concepts. Instead of just staring at symbols, you can see them come to life! For families, it can be a playful way to introduce kids to problem-solving. Imagine using a graph to decide on a movie time or a snack budget – you're exploring a range of possibilities together! And for hobbyists, whether you're into coding, crafting, or even gardening, knowing how to interpret these graphs can help you make more informed decisions. For instance, a gardener might use a compound inequality to represent the ideal temperature range for a specific plant to thrive.
Let's say you see a graph that looks like a line segment with filled-in circles at both ends. This often represents a compound inequality where numbers are between two values, including those two values themselves. For example, if the circles are at 5 and 10, and the line connects them, it could be saying that the number we're interested in is greater than or equal to 5 AND less than or equal to 10. In math terms, that's written as 5 ≤ x ≤ 10. Another variation might be an open circle at one end and a filled circle at the other, showing that one boundary is included, but the other isn't. Or perhaps two separate shaded regions, indicating that the number is either in one range OR another range – this is where the "compound" part really shines!
Getting started with interpreting these graphs is easier than you might think. First, identify the endpoints on the number line. These are the crucial boundaries. Next, look at the circles at those endpoints. Are they filled in (meaning the endpoint is included, usually with "or equal to") or open (meaning the endpoint is not included, just "less than" or "greater than")? Finally, observe the shading. Is it a continuous line between two points? Are there two separate shaded areas? This tells you if it's an "and" situation (numbers between) or an "or" situation (numbers in either region). You can even try sketching your own simple graphs based on everyday scenarios!
So, the next time you see a line or shaded region on a graph, remember it's not just squiggles; it's a visual story about numbers. Interpreting compound inequalities can add a layer of understanding and even enjoyment to various aspects of your life, making math feel a little less intimidating and a lot more practical.
