When Constructing An Angle Bisector Why Must The Arcs Intersect
Hey there, geometry geek! Or maybe you're just, you know, a human who sometimes has to draw a straight line. Either way, let's chat about something super cool. We're talking about angles. And not just any angles, but the ones you can bisect. That's a fancy word for splitting in half. Think of it like cutting a pizza, but with lines.
So, you've got your angle. Two lines meeting at a point, like a pointy hat. To split it perfectly in two, you need a special line. It's called the angle bisector. Pretty neat name, right? It’s like the VIP pass to the middle of the angle.
Now, how do we make this magical bisector? It’s not just about eyeballing it. Nope, we need some tools. A compass and a straightedge. The old-school tech. Think of them as your best buds for this mission.
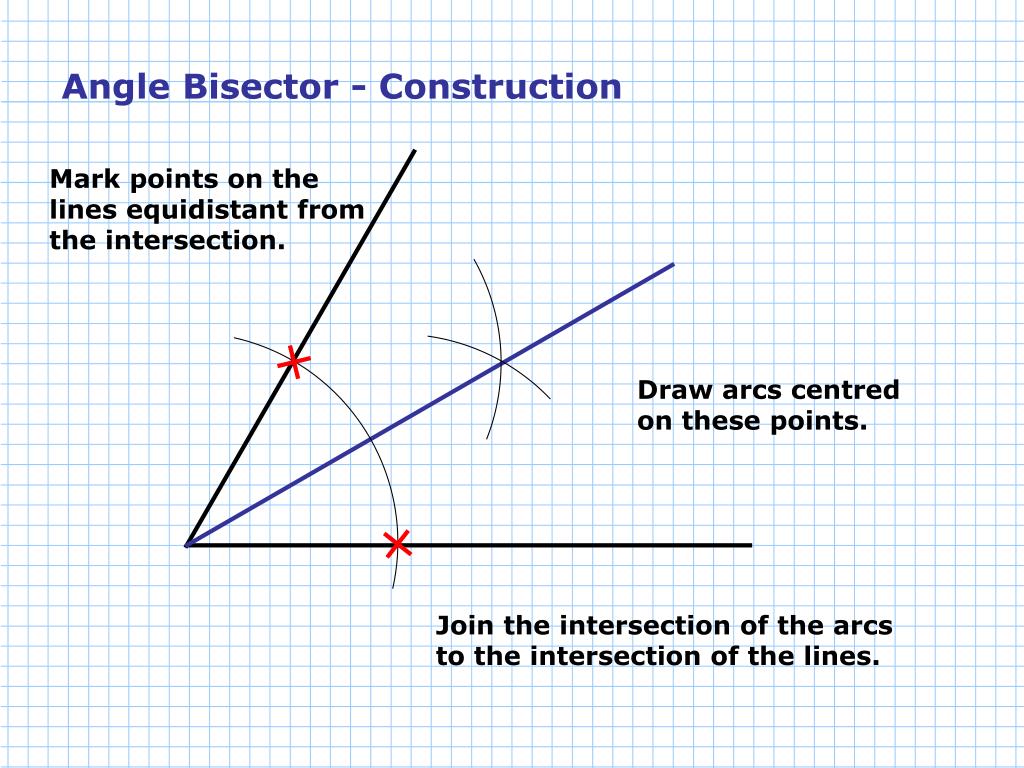
First step? You put your compass point on the vertex. That's the pointy tip of the angle. You open it up a bit. Not too much, not too little. Just right. Then, you draw an arc. This arc needs to cross both sides of your angle. Easy peasy.
This first arc is like saying, "Okay, angle, I see you. I'm marking your territory." It tells us that any point on this arc is the same distance from one side of the angle as it is from the other side.
But here’s where the real magic happens. We need a second step. And this is the part we’re really digging into today. The why. Why do we need more arcs? And why, oh why, do they have to cross?
After you draw that first arc, you move your compass. You don’t change the width of your compass. That's crucial. Think of it as keeping your secret weapon at the same strength. You move the compass point to one of the spots where your first arc hit the angle’s sides. Let's call these your "landing strips."
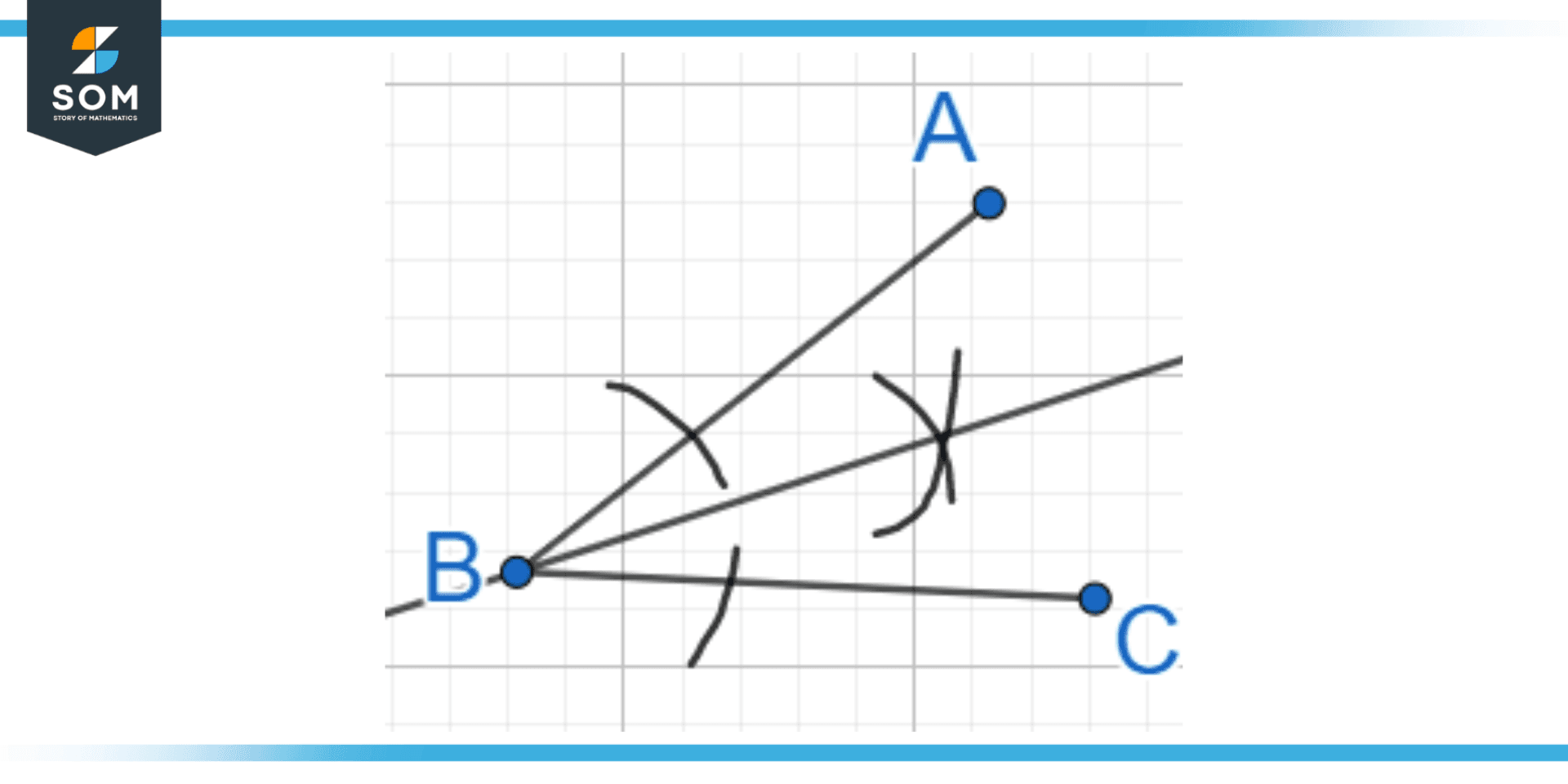
From that first landing strip, you draw another arc. This new arc is going to go inside your angle. It’s like a little whisper in the angle’s ear.
Then, you do it again. You move your compass to the second landing strip. Same compass width. And you draw a third arc. This one will also go inside the angle.
And here’s the big reveal! These two new arcs, the third and fourth arcs, are gonna meet. They're gonna cross each other. They’re gonna have a little get-together. They’ll have a point of intersection.
And that point? That intersection point? That’s your golden ticket. That’s the spot that’s going to be exactly halfway between the two sides of your original angle.
So, why the intersection? Why can't these arcs just do their own thing? Why must they collide? It's all about distance. Let's break it down. Remember the definition of a bisector? It’s a line that’s equidistant from both sides of the angle. Equally distant.

Think about the first arc. Every point on that arc is the same distance from side one of the angle as it is from side two. Makes sense, right? It’s like a sweet spot.
Now, when you move your compass to the first landing strip and draw that second arc, what are you saying? You’re saying, "All these points on this arc are a specific distance from this landing strip." And because that landing strip is already equidistant from both sides, you're creating a whole new set of potential midpoints.
But we need a point that is simultaneously equidistant from both sides and equidistant from the landing strip. It's like a double-threat location.
When you draw the third arc from the second landing strip, you're doing the same thing. You're saying, "All these points on this arc are a specific distance from that landing strip."

The intersection of these two arcs is the only place where both conditions are met at the same time. It's the cosmic handshake between your two arc-drawing missions.
Let's get a little geeky, but just for a sec. Imagine the two sides of your angle are lines, let's call them L1 and L2. The first arc creates a set of points that are equidistant from L1 and L2. This set of points is actually a segment of the angle bisector itself! Wild, right?
Now, let’s say your compass is set to a radius 'r'. When you put the compass on landing strip P1 (which is on L1 and L2), you draw an arc. Any point on this arc is distance 'r' from P1. When you do the same from P2, any point on that arc is distance 'r' from P2.
The point where these two arcs intersect is a point that is distance 'r' from P1 and distance 'r' from P2. And because P1 and P2 are symmetrically placed on the angle's sides, that intersection point must lie on the line that's perfectly in the middle.
It's like a treasure hunt. Each arc is a clue. The intersection is the X that marks the spot. If the arcs don’t intersect, it means either your compass wasn't opened wide enough, or you messed up the landing strips. It's a cosmic signal that something's amiss in geometry land.

Think of it this way: if you were trying to find a spot that's exactly halfway between two friends, and you both took steps in certain directions, you’d only meet at the middle if your steps were coordinated. The arcs are those coordinated steps.
The beauty of it is that this method is always going to work, as long as you do it right. It’s a foolproof system. A geometric guarantee. It’s proof that math can be elegant and practical at the same time.
And the quirky part? Even though it's a very precise geometric construction, it feels almost like drawing a smiley face or a simple star. There's a certain childlike joy in creating shapes with just a compass and a straightedge.
So, next time you need to bisect an angle, remember the dancing arcs. Remember their mission to intersect. They’re not just scribbles; they’re a conversation between distances, a pact to find the perfect middle. And that, my friend, is why the arcs must intersect. It's the universe's way of saying, "You've found the sweet spot!"
It’s a little bit of magic, a little bit of logic, and a whole lot of fun. Happy bisecting!
