What Is The Length Of Side Ab Of Parallelogram Abcd
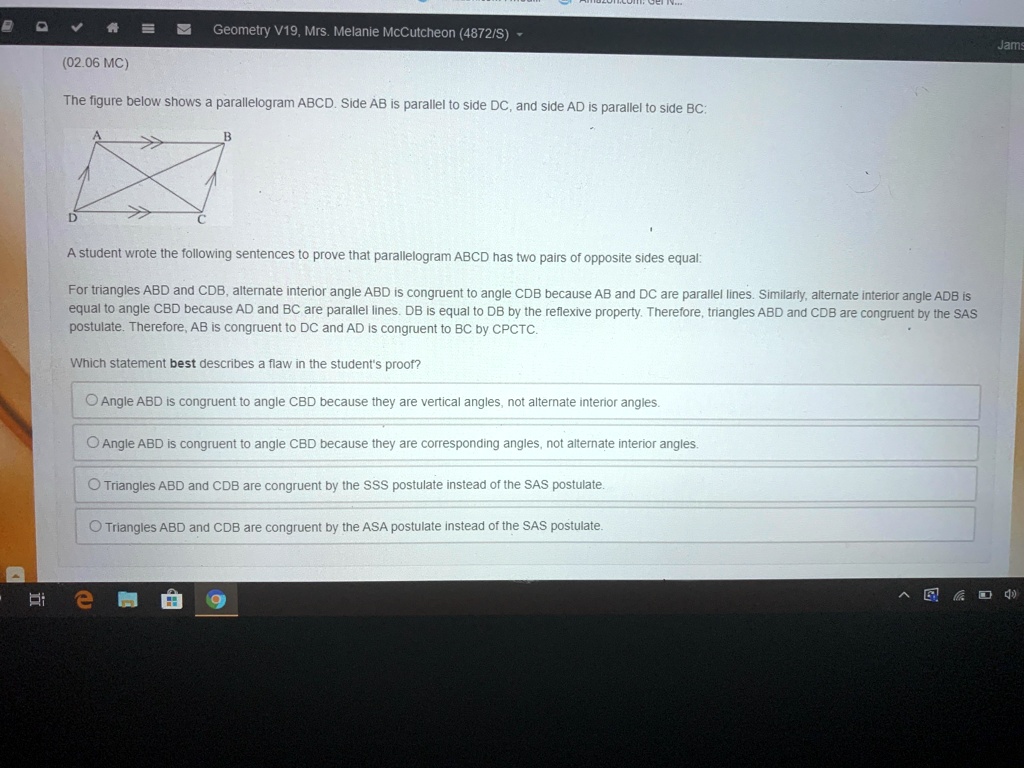
So, you're staring at a parallelogram, right? ABCD, to be exact. And your brain is doing that little whirr sound, asking, "Okay, but what's the deal with side AB?" It's a totally fair question! Like wondering how many jellybeans fit in a jar. Or if squirrels ever get tired of burying nuts. This whole parallelogram thing is pretty neat, though. It’s not just boring geometry. It’s got some personality!
Let's break it down. A parallelogram is like a slightly wonky rectangle. It's got four sides, and opposite sides are parallel. Think of train tracks. They never meet, right? That's parallel. And in a parallelogram, not only are opposite sides parallel, but they're also the same length. Mind. Blown. (Okay, maybe not blown, but it's a cool fact!)
So, back to our side AB. In parallelogram ABCD, AB is one of the sides. The one connecting point A to point B. Simple enough. But here's the kicker, the little secret handshake of parallelograms: side AB is exactly the same length as side DC. Yep. Those two opposite sides? Twinsies!
Why is this fun? Because it's like a tiny puzzle piece clicking into place. You see ABCD, and instantly, you know something about AB just by looking at DC. No complicated calculations needed. It's like having a superpower, but for shapes. Your friends might be scratching their heads, and you're there like, "Oh, that? That's just how parallelograms roll."
The Quirky Charm of Parallelograms
Parallelograms aren't just about lengths. They're also about angles. Opposite angles are equal, too! So, angle A is the same as angle C. And angle B is the same as angle D. It's all about symmetry. A bit like a perfectly balanced seesaw. Except, you know, with straight lines and corners.

And here's a funny thought: if you try to push on a rectangle, it resists. It wants to stay a rectangle. But a parallelogram? It's a bit more flexible. You can shear it. Imagine pushing on the top of a deck of cards. It slumps over, right? That's a parallelogram in action. It's got that give. That's why they're used in things like folding chairs and retractable gates. They can change shape without breaking.
Think of your favorite parallelogram. Maybe it's a slightly tilted window frame. Or a slice of pizza that’s a bit too enthusiastic with its lean. Every parallelogram has its own unique charm. And the length of its sides is part of that story.
So, How Do We Know the Length of AB?
This is where things get really interesting. The question "What is the length of side AB of parallelogram ABCD?" is like asking "How long is a piece of string?" There's no single answer! It depends entirely on the specific parallelogram you're looking at. It's not a universal constant, like the speed of light (which is way more complicated anyway).
To know the length of AB, you need more information. You might be given the length of side DC. Since they're equal, easy peasy! Or, you might be given the lengths of the adjacent sides, like AB and BC. In that case, AB could be any length, and BC could be any length. They just have to be opposite each other and parallel.
Sometimes, you might get a diagram with some numbers on it. That's a good sign! Or, the problem might state something like, "In parallelogram ABCD, side AB measures 5 units." Then, boom! You know AB is 5 units. And because of that amazing parallelogram rule, you also know DC is 5 units. High fives all around!
It’s like a secret code. You’re given one piece of the puzzle, and the properties of the parallelogram unlock the rest. It's detective work, but with shapes instead of footprints. And way less mud involved. Hopefully.

Why This Matters (Sort Of!)
Okay, let’s be honest. For most of us, knowing the exact length of side AB of a random parallelogram might not change our daily lives. You're probably not going to be measuring parallelograms on your commute. Unless your commute is exceptionally geometric.
But it's fun because it teaches us to observe. To look at shapes and understand their rules. It’s about noticing patterns. And in a world that can sometimes feel chaotic, finding order in shapes is strangely comforting. It's a little bit of predictable beauty.
Plus, understanding these basic properties is the stepping stone to cooler stuff. Like calculating the area of a parallelogram. Or understanding how they’re used in engineering, art, and even music (seriously, look up tessellations!). It all starts with these fundamental facts.

The Secret Life of Side AB
So, the length of side AB of parallelogram ABCD is not a fixed number. It's a variable! It's a character in the story of that particular parallelogram. It could be tiny, like a ladybug's shadow. Or it could be huge, like a billboard. It all depends on who its parallelogram buddies are.
But the rule? That AB is equal to DC? That's constant. That's the reliable friend in the parallelogram group. It's the anchor. It’s what makes a parallelogram a parallelogram. Without that rule, it's just a lumpy quadrilateral. And where's the fun in that?
Next time you see a parallelogram, give a little nod to side AB. Acknowledge its existence. And remember its twin, DC. They’re the silent, equal partners holding the whole thing together. It’s a small detail, but it's a pretty awesome detail. And that's why we talk about it. Because geometry, when you look at it the right way, is anything but boring. It's full of little surprises. Just like finding an extra fry at the bottom of your fast-food bag. Pure, unexpected joy. Or, you know, the length of side AB.
