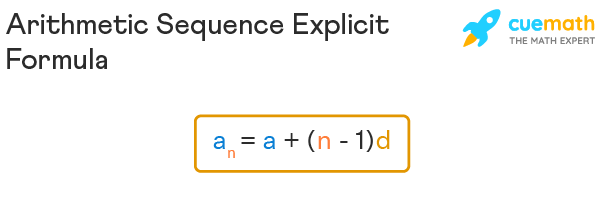What Is The Explicit Formula For The Arithmetic Sequence Mc017-1.jpg

Ever found yourself staring at a list of numbers that seems to have a secret superpower? You know, the kind where you can predict what’s coming next with uncanny accuracy? That, my friends, is the magic of an arithmetic sequence! And let me tell you, figuring out the exact number way, way down the line, without having to painstakingly count every single step, is like unlocking a cheat code for numbers. Today, we're diving headfirst into the marvelous world of the explicit formula for these sequences. Prepare to have your mind gently tickled and your numerical confidence boosted!
Imagine this: you’re at a bake sale, and the cookies are flying off the shelves. The first customer buys 3 cookies. The next, eager for more, buys 5. Then another buys 7. See the pattern? It’s like the cookie vendor has a secret recipe for enticing customers – adding 2 more cookies each time! This is a classic arithmetic sequence. The numbers are 3, 5, 7, and if we’re lucky, the next person will buy 9, then 11, and so on. It’s a steady, predictable climb, like a perfectly baked soufflé rising in the oven.
Now, what if you wanted to know how many cookies the 100th customer would buy? Are you going to stand there and count 3, 5, 7, 9… all the way to 100? No way! That’s where our superhero, the explicit formula, swoops in to save the day. It’s like a super-fast calculator that can jump straight to any number in the sequence, no matter how far down the line it is. Think of it as a magical crystal ball for numbers!
So, what is this magical formula? Drumroll please… It’s:
an = a1 + (n - 1)d
Now, I know what you might be thinking. "Whoa, what are all these fancy letters?" Don't let them scare you! They're just shorthand for the important players in our arithmetic sequence game.

Let's break them down. First up, we have a1. This is simply the first number in your sequence. In our cookie example, that would be the initial 3 cookies. It’s the starting point, the launchpad for our numerical rocket. Easy peasy, right?
Next, we have n. This is the position of the number you're interested in. So, if you want to know about the 100th customer, n would be 100. It’s the target, the destination we're aiming for in our sequence journey.
And then there’s d. This is perhaps the most important player in our arithmetic sequence team. It’s called the common difference. This is the constant amount that gets added (or subtracted, if the sequence is going down) between each number. In our cookie example, the difference between 3 and 5 is 2. The difference between 5 and 7 is also 2. So, our common difference, d, is 2. It’s the secret sauce, the consistent step that keeps the sequence marching along!
Finally, an is the grand prize! It’s the actual number at that specific position n. It’s what we’re trying to find – the number of cookies the 100th customer will buy, for instance.

Let’s put our cookie example to the test. We want to find out how many cookies the 100th customer buys. So, we have:
- a1 (the first number of cookies) = 3
- n (the position we're interested in) = 100
- d (the common difference) = 2
Now, plug these into our amazing formula:
a100 = 3 + (100 - 1) * 2
Fórmula Aritmética Explícita Full Article: The Impact Of Two
Let's do some super simple math. First, we handle the stuff inside the parentheses: 100 - 1 = 99.
a100 = 3 + 99 * 2
Next, we multiply: 99 * 2 = 198.
a100 = 3 + 198
Arithmetic Sequence Explicit Formula - Formula, Derivation, Examples
And finally, we add: 3 + 198 = 201.
Voila! The 100th customer will buy a whopping 201 cookies! Can you believe it? We skipped all the tedious counting and jumped straight to the answer. It's like having a direct express train to the end of the number line!
This formula is your best friend whenever you see a sequence where the difference between consecutive numbers is always the same. Think about counting your steps while walking: 1, 2, 3, 4… the difference is always 1! Or maybe you’re saving money, and you add $10 to your piggy bank every week. That’s an arithmetic sequence too! The explicit formula is your trusty sidekick, ready to calculate any future amount with impressive speed and accuracy.
So next time you spot a pattern that’s adding or subtracting the same amount each time, don’t panic. Just remember your friend, the explicit formula, and you'll be solving numerical puzzles like a pro in no time. It’s a little piece of mathematical magic that makes the world of numbers just a little bit more predictable, and a whole lot more fun!