What Is The End Behavior Of The Polynomial Function Brainly

Ever wondered what happens to a polynomial function when things get super, super big or super, super small? Like, when the input number (we call that 'x') goes way, way off to the right on a graph, or way, way off to the left? That's basically what we're talking about with end behavior. It's like the ultimate fate of the polynomial's journey! Think of it as the polynomial's grand finale, its farewell performance on the graph.

Now, the cool thing about end behavior is that it's actually pretty predictable. You don't need to do super complicated math to figure it out. It's all about looking at just one little part of the polynomial: the leading term. This is the term with the biggest exponent. It's the boss of the polynomial, the one that calls the shots when 'x' gets enormous.

Imagine a polynomial is like a fancy, winding road. The end behavior tells you what the road looks like way, way out there, far from where all the little twists and turns happen. Does it go up forever? Does it go down forever? Or maybe it's a bit more dramatic, going up on one side and down on the other. It’s like peeking around the corner to see where the road is headed.

So, how do we figure out this grand finale? It’s all thanks to two main things about the leading term: its sign (is it positive or negative?) and the parity of its exponent (is the exponent an even number or an odd number?). These two little details are the secret ingredients to predicting the end behavior.

Let's break it down. First, we look at the exponent of the leading term. Is it even, like 2, 4, 6, or odd, like 1, 3, 5? This is like deciding if the polynomial's journey is going to be smooth and symmetrical on both ends, or if it's going to be a bit more of a dramatic, opposite climb and descent.

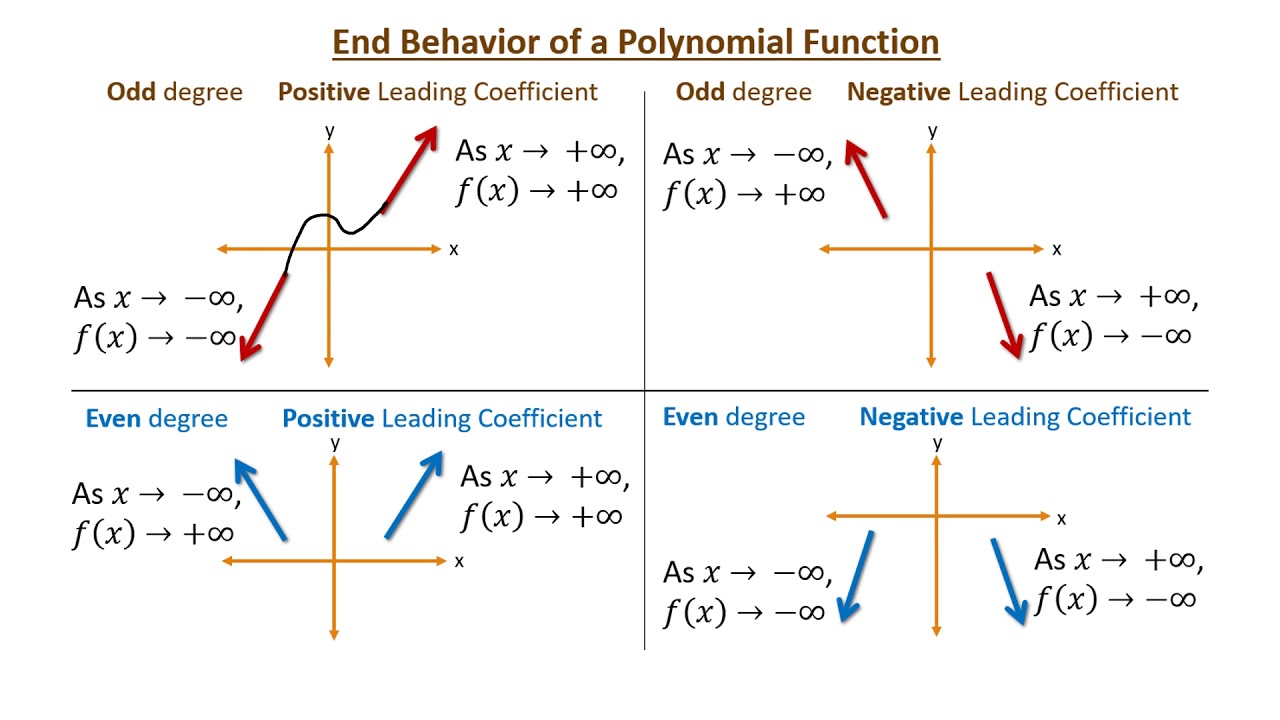
If the exponent is even, things tend to be symmetrical. Think of a 'U' shape. Both ends of the 'U' go in the same direction. If the leading term is positive, both ends of the polynomial go up, up, up towards positive infinity. It’s like a giant smile stretching across the graph! If the leading term is negative, both ends go down, down, down towards negative infinity. It's like a sad frown, or a valley getting deeper and deeper.

The leading term is the superstar of end behavior!

Now, what if the exponent is odd? This is where things get more interesting and a little less symmetrical. The ends of the polynomial will go in opposite directions. If the leading term is positive, one end goes down towards negative infinity (as 'x' gets super small, or goes left), and the other end goes up towards positive infinity (as 'x' gets super big, or goes right). It’s like a rollercoaster starting at the bottom and climbing to the very top! If the leading term is negative, it’s the opposite: one end goes up (as 'x' gets super small), and the other end goes down (as 'x' gets super big). Imagine a rollercoaster that starts at the top and dives all the way down.

So, to sum it up, there are really only four possible end behaviors for any polynomial function:

1. Both ends go up (positive leading term, even exponent).
2. Both ends go down (negative leading term, even exponent).
3. Left end goes down, right end goes up (positive leading term, odd exponent).
4. Left end goes up, right end goes down (negative leading term, odd exponent).

It's like a simple dance with just a few basic steps. The bigger and more complex the polynomial gets, the more the middle part might wiggle and jiggle with all sorts of interesting turns. But the end behavior? That’s like the steady, predictable fade-out at the end of a song. It's always going to follow one of those four patterns.

Why is this so entertaining? Because it gives us a sneak peek into the overall shape of the graph! Before we even plot a single point, we can predict where the graph is heading in the long run. It’s like having a map that shows you the general direction of a journey, even if you can’t see every single mile marker. It helps us understand the "big picture" of the polynomial.

Think about it: a cubic function (like $y = x^3$) has an odd exponent and a positive leading coefficient. So, its end behavior is that it goes down to the left and up to the right. Simple! A quadratic function (like $y = x^2$) has an even exponent and a positive leading coefficient. So, both ends go up. Easy peasy!

The "Brainly" aspect of this, or where you might encounter it when looking for help online, is that understanding end behavior is a fundamental building block for graphing and analyzing polynomial functions. It’s a common question because it’s crucial for grasping how these functions behave on a larger scale. People often ask about it to get a quick handle on the overall trend of a function without getting lost in the details of every single bump and dip.

What makes it special is its simplicity amidst complexity. Polynomials can look super complicated with lots of terms and high powers. But their end behavior boils down to just a few rules. It’s a bit like the saying, "The more things change, the more they stay the same." The middle part of the polynomial can be a wild ride, but the ends are remarkably consistent.

It’s also special because it’s a gateway to understanding more advanced mathematical concepts. Once you’ve got a handle on end behavior, you can start to think about things like asymptotes and the overall shape of curves. It’s like learning your ABCs before you can read a novel.

So, next time you see a polynomial, don’t be intimidated! Just look for that leading term. Check the exponent's parity and the coefficient's sign. You'll instantly know where that graph is heading in the long, long run. It’s a little bit of mathematical magic, revealing the predictable secrets of the function's ultimate destiny. It’s a fun little puzzle to solve, and the answer is always right there, staring you in the face from the polynomial's most powerful term. Give it a try – you might find it surprisingly delightful!