Use The Laws Of Logarithms To Expand The Expression

Ever stare at a math problem and feel like you're trying to untangle a giant ball of Christmas lights in the dark? You know, the kind where one knot leads to another, and suddenly you're questioning all your life choices? Well, guess what? Those magical little things called logarithms are like your super-powered scissors for those tangles! Today, we're going to have some serious fun with them, specifically by learning how to expand expressions. Think of it as taking a tiny, tightly packed gift and unwrapping it into a whole pile of awesome presents!
Let's imagine you have a super-secret recipe, and it's all written down in a complicated code. This code uses a special base number, let's call it the "Magic Base", and then it has all these numbers and operations crammed together. For example, you might see something that looks like logMagic Base(ingredient1 * ingredient2). Now, that looks like a mouthful, right? It’s like trying to order a latte in a language you barely know. But fear not, because our Laws of Logarithms are here to save the day, turning that confusing jumble into something much more manageable, even... dare I say... fun!
Our first superhero in this log-tastic adventure is the Product Rule. Imagine you're at a fantastic all-you-can-eat buffet, and you've got a plate piled high with two amazing dishes: "Delicious Donuts" and "Sensational Spaghetti". In logarithm land, this is like having log(Donuts * Spaghetti). The Product Rule whispers sweetly, "Hey! Don't keep them together! You can have your donuts separately and your spaghetti separately!" So, that intimidating log(Donuts * Spaghetti) magically transforms into log(Donuts) + log(Spaghetti). See? It’s like finally being able to enjoy each delectable bite of your buffet without feeling guilty about mixing them all up! You've just expanded your joy (and your math expression)!
Next up, we have the Quotient Rule. This one is perfect for when you're sharing something, like a gigantic, mind-blowingly delicious pizza. Let's say you have log(Pizza / Pepperoni). This means you're trying to figure out something about the pizza divided by the pepperoni. The Quotient Rule swoops in and says, "Why be stingy? Let's separate those! You can have the goodness of the log(Pizza) and then subtract the sheer deliciousness of the log(Pepperoni)!" So, our expression becomes log(Pizza) - log(Pepperoni). It’s like saying, "I love the whole pizza, but I also have a special appreciation for the pepperoni, and I can think about them independently!" No more feeling overwhelmed by the division; we've split it into simpler, more understandable parts.
Now, let's talk about the Power Rule. This one is like discovering you have a secret superpower that lets you multiply things by themselves over and over! If you see something like log(AwesomeStuff3), it means you have "Awesome Stuff" multiplied by itself three times. The Power Rule is your enthusiastic cheerleader, shouting, "Why do the multiplying yourself? Just bring that '3' down and let it do the work for you!" So, log(AwesomeStuff3) becomes 3 * log(AwesomeStuff). It's like going from doing 10 push-ups to just telling someone to do 3 push-ups for you. Effortless efficiency, folks!
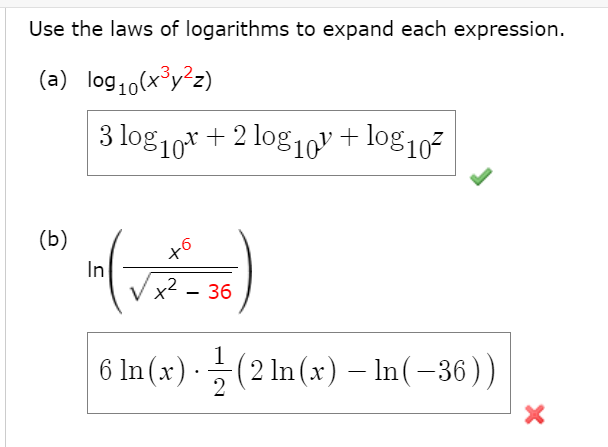
Let's put it all together with a slightly more complex, but still totally manageable, example. Imagine you have this beast: log10( (x2 * y) / z ). Don't let the 10 scare you; that's just our "Common Logarithm" friend, base 10, showing up to play. First, we spot that division inside. That calls for the Quotient Rule! We break it apart like so: log10(x2 * y) - log10(z). Now, look at that first part: log10(x2 * y). We've got multiplication! Time for the Product Rule! That becomes: log10(x2) + log10(y). So, our expression is now: log10(x2) + log10(y) - log10(z). But wait, there's a pesky exponent on that 'x2'! You know what that means – the Power Rule to the rescue! We bring that '2' down and out: 2 * log10(x).
And voilà! Our monstrous expression has been beautifully expanded into: 2 * log10(x) + log10(y) - log10(z). See? We took a complicated log-tangle and turned it into a neat little line of simpler logs. It’s like transforming a messy room into a perfectly organized workspace. You’re not doing more work; you’re just making the work you are doing so much easier to understand and manipulate. So, the next time you see a logarithm expression that looks like it could win a wrestling match, remember your log rules. They’re not just math; they’re your secret weapon for conquering complexity with a smile and a sprinkle of mathematical glee!
