Use The Function Below What Are The Amplitude And Midline
So, picture this: you're at a swanky café, the kind where the barista knows your name and your secret desire for extra foam. You've just ordered your ridiculously overpriced latte, and you're contemplating the universe, or maybe just whether to get a second croissant. Suddenly, your brain, being the perpetually curious (and slightly unhinged) organ it is, throws a curveball at you. It whispers, "Hey, remember that math stuff? Yeah, let's dive into amplitude and midline." And just like that, your peaceful café moment is interrupted by a flashback to high school trigonometry. Don't worry, though, because we're about to demystify these two terms in a way that won't involve chalk dust or the existential dread of a pop quiz. Think of this as your secret decoder ring for the wild world of functions, delivered with a side of humor and maybe a sprinkle of caffeine-fueled enlightenment.
First off, let's talk about the amplitude. Now, if you're imagining a rock star dramatically stomping on stage, you're not entirely wrong. Amplitude, in the world of functions, is basically the height or intensity of the wave. Think of it as how much your function decides to go wild, how far it swings up from its resting point and how far it plunges down. It’s the funkiness factor, the "wow" element of the graph.
Imagine a perfectly calm lake. That's your function chilling out, probably at its midline. Now, a speedboat zooms by, creating waves. The amplitude is how tall those waves get from the surface of the lake. Big boat, big waves, big amplitude! Small ripple from a duck? Tiny amplitude. Easy peasy, right? It's the maximum displacement from the center, the peak of the party, or the deepest dive into the existential abyss, depending on the function's mood.
Now, there's a secret little trick to calculating amplitude. If you’ve got a function that’s doing its wave-like thing, you can find the highest point (the maximum) and the lowest point (the minimum). The amplitude is simply half the difference between those two extremes. So, you take the tallest peak, subtract the deepest valley, and then divide by two. It’s like finding the halfway point between being on top of the world and feeling like you’ve just stubbed your toe on a furniture leg. (Maximum - Minimum) / 2 = Amplitude. And there you have it! You've just tamed the wild beast of amplitude. Give yourself a pat on the back. Maybe even treat yourself to that second croissant.
Okay, moving on! Let's talk about the midline. If amplitude is the height of the swing, the midline is the center line around which that swing happens. It's the happy medium, the equilibrium, the place where your function takes a breather before its next dramatic performance. Think of it as the average position, the calm eye of the storm, or the stage your rock star is standing on before they launch into their epic guitar solo.
Imagine a swing set in the park. When it's not moving, it’s hanging at a certain height, right? That’s its midline. When you push someone on the swing, they go up and down, but they always swing around that resting point. The midline is that resting point. It’s the line that cuts the wave perfectly in half, horizontally speaking. It's the reference point, the anchor that keeps your function from floating off into the mathematical ether.
Calculating the midline is even easier than its amplitude buddy. It’s just the average of the highest and lowest points. You add up the maximum and minimum values and then divide by two. So, if your function reaches a peak of 10 and a valley of -2, the midline is (10 + (-2)) / 2 = 8 / 2 = 4. It's like finding the sweet spot, the balanced point of balance. (Maximum + Minimum) / 2 = Midline. See? It's not brain surgery. It's more like… brain pastry. Much more delicious.
So, why do we even care about amplitude and midline? Well, they’re like the basic personality traits of a function. They tell us a lot about its behavior. Amplitude tells us how extreme the function gets, while the midline tells us where its average or resting position is. For example, in physics, amplitude can represent the loudness of a sound wave or the brightness of light. Midline? That’s just the baseline, the ambient hum of the universe.
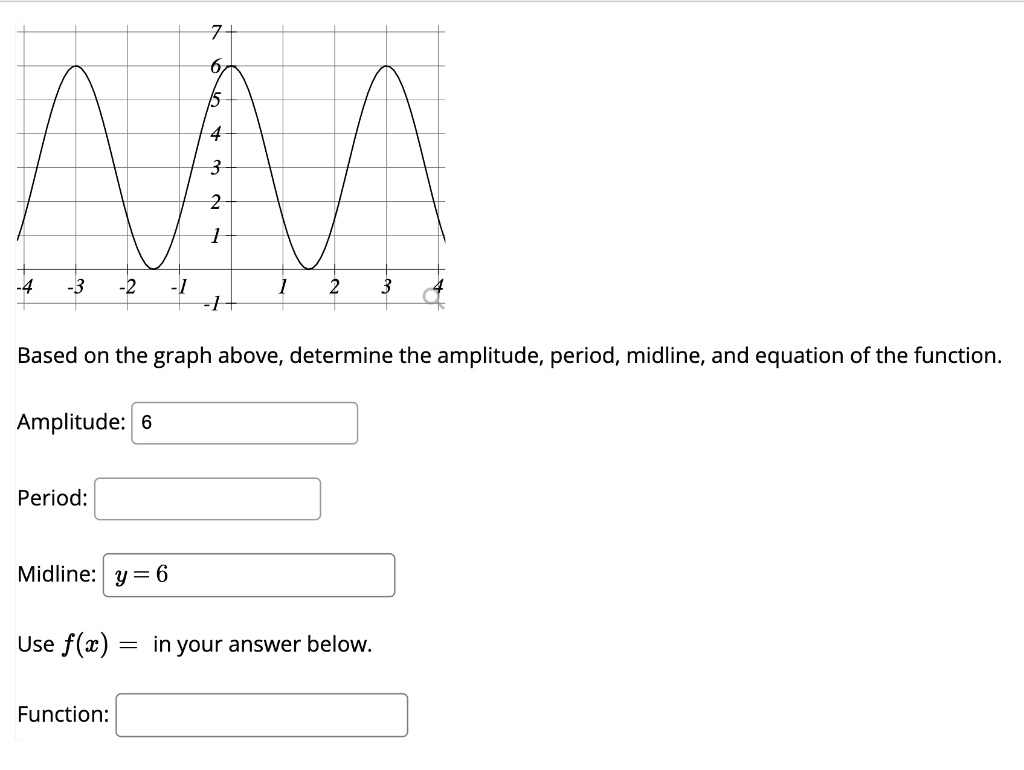
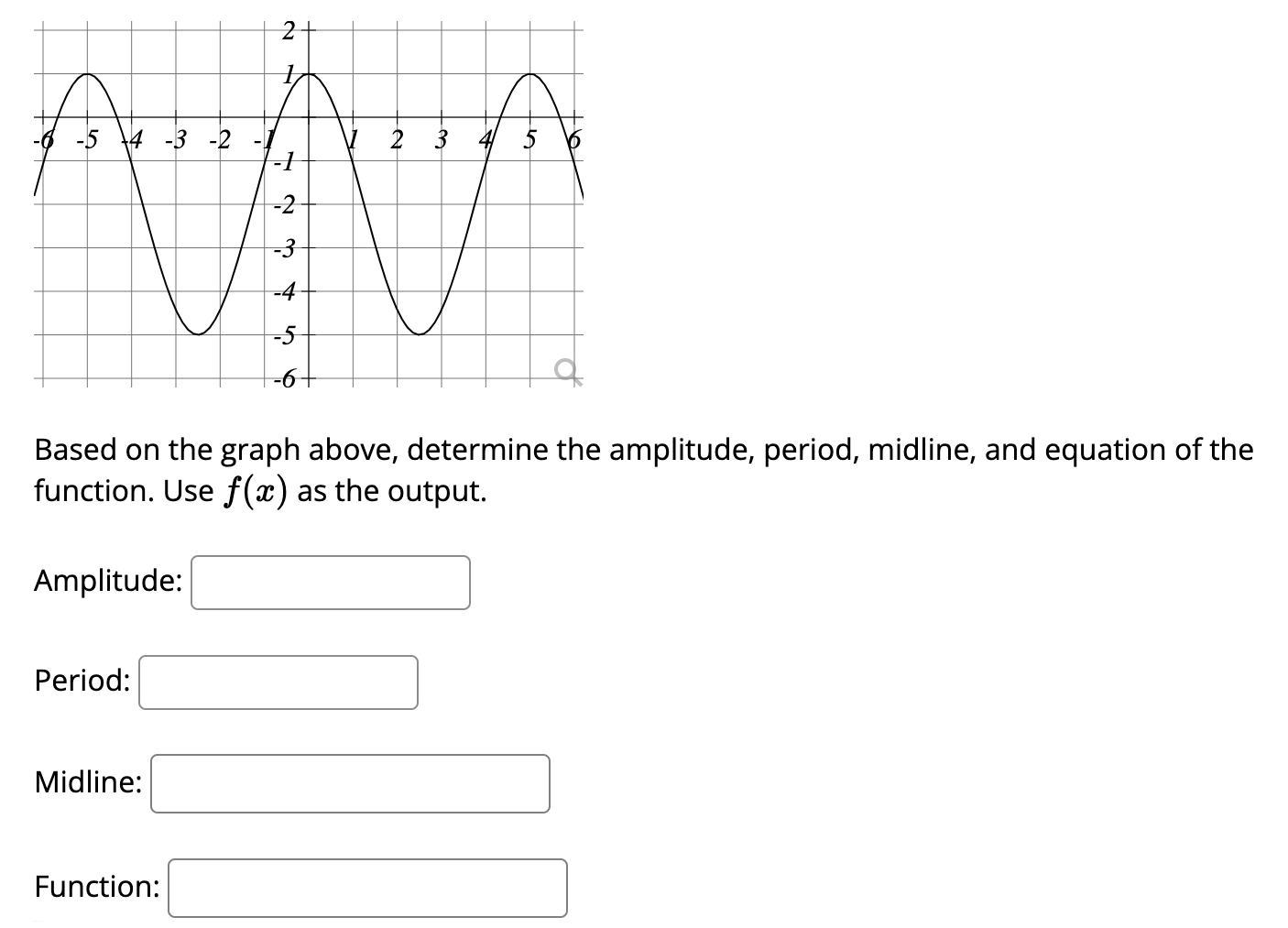
Think about a sine wave, that classic S-shaped curve. If you have a function like y = 5sin(x), the amplitude is 5. That means the wave swings 5 units up and 5 units down from its center. And since there’s no extra number added or subtracted outside the sine function, the midline is simply 0 (the x-axis). It's a perfectly balanced wave doing its thing.
Now, what if we change it up a bit? Let's say we have y = 3sin(x) + 2. What happened there? Well, the '3' in front of the sine function is our new amplitude. So, the wave swings 3 units up and 3 units down. But that '+ 2' at the end? That's our midline shifter! It means the entire wave has been pushed up by 2 units. So, instead of being centered at y=0, this wave is now centered at y = 2. The highest point will be 2 (midline) + 3 (amplitude) = 5, and the lowest point will be 2 (midline) - 3 (amplitude) = -1. See how they work together like a perfectly coordinated dance duo?
It's like a really dramatic opera singer. Their voice has a certain amplitude – how loud and powerful they can belt it out. But they're also singing within a certain vocal range, and the midline could be considered their average pitch, the note they often return to. If they suddenly start hitting notes that are way higher or lower than usual, that's a change in amplitude. If their entire performance is just shifted to a higher or lower key, that's a change in the midline. And if they do both? Well, then you’ve got a truly captivating performance, or possibly a very confusing math problem.
The cool thing is, this applies to more than just abstract math graphs. Think about the tides. They go up and down, right? The amplitude is how much the water level changes from its average. The midline is that average sea level. Or consider the stock market – some stocks are super volatile (big amplitude!), while others are pretty steady (small amplitude!). And the general trend of the market over time could be considered its midline. Okay, maybe not exactly like the stock market, but you get the drift. It's about understanding the ups and downs and the resting state.
So, next time you see a wavy graph, or someone mentions amplitude and midline, don't panic. Just think of the calm lake, the swinging child, the opera singer, or even your own caffeine-fueled energy levels throughout the day. Amplitude is the swing, the drama, the sheer audacity of the function. Midline is the anchor, the calm center, the place it calls home. And together, they paint a pretty clear picture of what’s going on. Now, about that second croissant…
