Use The Distributive Property To Rewrite Each Expression
Alright, gather 'round, you magnificent mathematical misfits! Today, we're diving headfirst into the wonderfully wacky world of the distributive property. Now, I know what you're thinking. "Distributive property? Sounds like something a sad clown would do on a Tuesday." But fear not, my friends, because this isn't about sad clowns (unless you want it to be, we can totally make it about sad clowns). This is about making math way, way easier, and maybe even a little bit fun. Think of me as your friendly neighborhood math whisperer, here to decode the arcane arts of algebra.
Imagine you're at a café, right? The barista, bless their caffeinated soul, brings you your order. They've got a perfectly frothed latte and a freshly baked croissant. Now, what if they said, "Here's your latte, and here's your croissant, but I'm also going to distribute the goodness of this entire bakery to you." That's kind of what the distributive property does, but with numbers. It's like taking one thing and making sure it touches everything else it's supposed to. Revolutionary, I tell you!
Let's get down to the nitty-gritty, shall we? The basic idea behind the distributive property is that when you have a number or a variable hanging out outside a set of parentheses, it's eager to get to know what's inside. It wants to be distributed to each and every term within those parentheses. It’s like a popular kid at a party, wanting to say hi to everyone. Nobody gets left out!
So, you've got an expression that looks something like this: a(b + c). See that 'a' chilling outside the parentheses? It's got places to be, people to see. It's going to multiply with 'b', and then it's going to multiply with 'c'. And the result? Ta-da! It becomes ab + ac. Mind. Blown. It's like magic, but with more logic and significantly fewer rabbits being pulled out of hats. Although, if you can somehow make numbers disappear and reappear, please, for the love of all that is good, share your secrets.
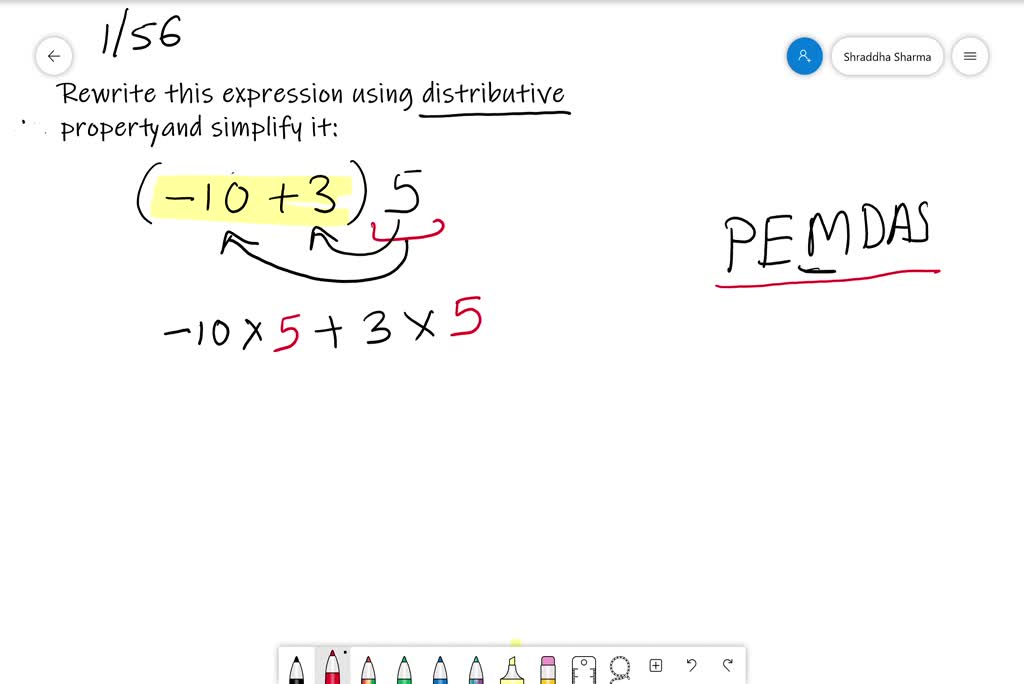
Let's try a slightly more exciting example. Imagine you're buying snacks for a movie marathon. You decide to buy 3 bags of popcorn and 3 boxes of candy. The cost of each bag of popcorn is $5, and the cost of each box of candy is $2. How much are you spending in total? You could, of course, calculate the popcorn cost (3 * $5 = $15) and the candy cost (3 * $2 = $6) and then add them up ($15 + $6 = $21). That's perfectly fine. But then you'd be missing out on the sheer joy of the distributive property!

We can rewrite this as 3(5 + 2). See? The 3 represents the number of each snack you're buying. Now, that 3 is outside the parentheses, just itching to get involved. It's going to multiply with the 5 (the popcorn cost) and then multiply with the 2 (the candy cost). So, it becomes (3 * 5) + (3 * 2). That’s 15 + 6, which still equals $21. But doesn't it feel a little more… elegant? Like you’re a math ninja, striking with precision and flair?
This property is a lifesaver, especially when you start dealing with bigger numbers or variables. Imagine trying to calculate 7 times 102 without a calculator. Brutal, right? Your brain might start staging a rebellion, demanding a nap and a strong cup of tea. But with the distributive property? Piece of cake. You can rewrite 102 as (100 + 2). So, the problem becomes 7(100 + 2).
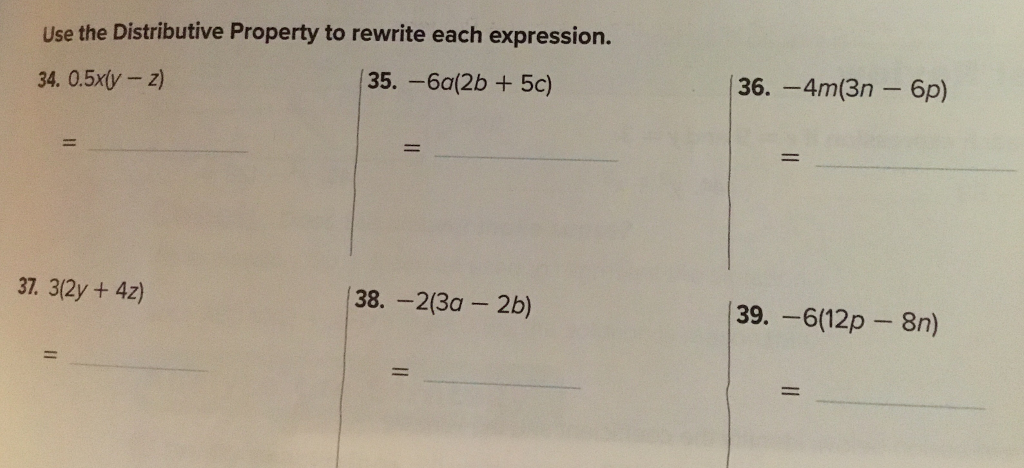
Now, distribute that 7! We've got (7 * 100) + (7 * 2). That's 700 + 14. And what do you know? You've got 714! See? No calculator required. Your brain is still in one piece, and you've just conquered a seemingly daunting task. It’s like finding a secret passage in a ridiculously complicated maze. "Huzzah!" you cry, as you emerge victorious.
Let's sprinkle in some variables, because that's where things get really exciting (in a nerdy, math-loving way, of course). Say you have the expression 4(x - 3). The 4 wants to spread its love to both 'x' and '-3'. So, it becomes (4 * x) - (4 * 3). And what does that simplify to? You guessed it: 4x - 12. It's like the 4 is a tiny, bossy manager, making sure both 'x' and the number 3 get their fair share of multiplication. "You do this! And you do that!"

What about when there are negative numbers involved? Ah, the plot thickens! Let's take -2(y + 5). The -2 is feeling a little moody, so it's going to distribute that grumpiness to everything inside. So, it's (-2 * y) + (-2 * 5). And that, my friends, is -2y - 10. Notice how the negative sign stuck with the 2. It’s a loyal companion. It’s like a shadow, always there. Sometimes it's a helpful shadow, sometimes it's… well, a negative shadow. But it’s always there.
Here’s a slightly trickier one: 3(2a + 5b - 7). Don't panic! This is like a buffet for the number 3. It's going to sample everything. So, we get (3 * 2a) + (3 * 5b) - (3 * 7). And simplifying that gives us 6a + 15b - 21. See? The distributive property is the ultimate peacemaker, ensuring every term inside gets its due. It’s the UN of the algebraic world, brokering peace and balance through multiplication.

Now, sometimes you might see something like (x + 2)(x + 3). This looks a bit different, right? There are two sets of parentheses. But fear not, for the distributive property is still your best friend! It's just applied a little more… thoroughly. Think of it as a double-whammy distribution. The first term in the first parentheses (the 'x') needs to multiply with both terms in the second parentheses (the 'x' and the '3'). Then, the second term in the first parentheses (the '2') also needs to multiply with both terms in the second parentheses.
So, for (x + 2)(x + 3): First, the 'x' from the first set: x * (x + 3) which gives us x² + 3x. Then, the '2' from the first set: 2 * (x + 3) which gives us 2x + 6. Now, you just add those results together: (x² + 3x) + (2x + 6). And if you’re feeling fancy, you can combine the like terms (the '3x' and the '2x'): x² + 5x + 6. It’s like a whole algebraic family reunion, and everyone’s getting to know everyone else through multiplication!
The distributive property is everywhere, lurking in the shadows of your math problems, waiting to be unleashed. It's the secret sauce that makes complex equations manageable and opens up a whole new universe of mathematical possibilities. So next time you see a number hanging out by some parentheses, give it a friendly nod, unleash the distributive property, and watch the magic happen. You'll be rewriting expressions like a pro in no time. And who knows, you might even start seeing the world in terms of distributed properties. That parking spot is distributed among the other cars. That slice of pizza is distributed among your friends. It's a beautiful, mathematical life!
