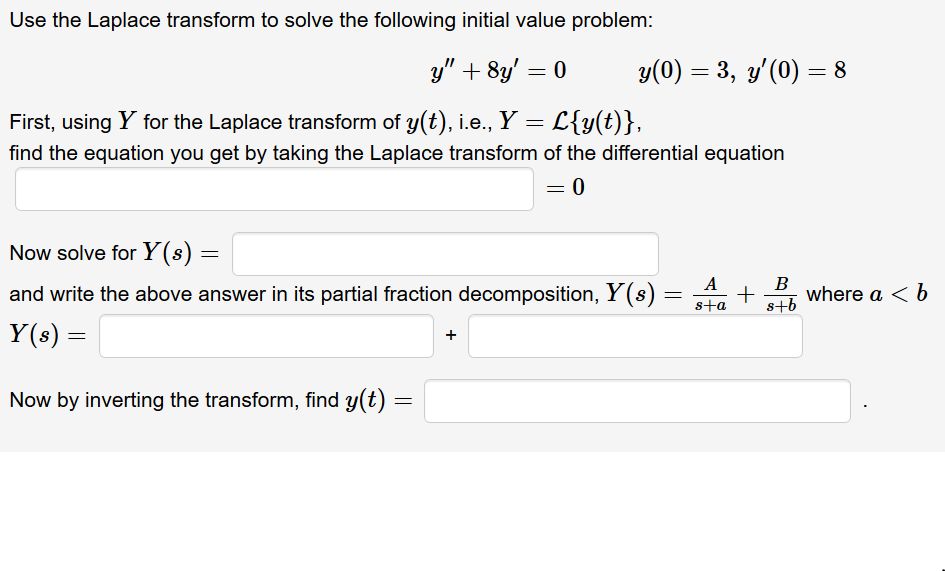
Use Laplace Transforms To Solve The Following Initial Value Problems
Imagine you've got a super complicated toy, like a robot that’s gone haywire. It's whirring, it's beeping, it’s doing all sorts of unpredictable things, and you just want to get it back to its normal, happy state. You've tried nudging it, you’ve tried shaking it, but nothing seems to work. This is where our superhero, Laplace Transforms, swoops in to save the day!
Now, you might be thinking, "Laplace Transforms? Sounds like something out of a sci-fi movie!" And in a way, it is! Think of it as a magical spell that takes a really messy, real-world problem and transforms it into a simpler, easier-to-manage problem in a whole new dimension. It’s like turning a chaotic symphony into a simple arithmetic problem. And the best part? Once you solve the simple problem, you can magically transform the answer back into the solution for your original, messy situation.
Let's say our haywire robot’s movements are described by a tricky equation – a differential equation. These equations are like the secret instructions that govern how things change over time. They can be tough nuts to crack. But Laplace, our friendly wizard, has a secret handshake with these equations. When you apply his magic spell (the Laplace Transform), the differential equation, with all its messy derivatives and functions, gets turned into a much friendlier algebraic equation. Algebra? We've all done that in school, right? It’s like going from deciphering ancient hieroglyphs to reading a children's book.
And what’s so great about this new algebraic world? Well, in this transformed world, things are much calmer. We can solve for our unknown, which represents the state of our robot, with relative ease. It's like finding a lost key in a neatly organized drawer instead of a cluttered attic. We can use all sorts of familiar algebraic tricks and techniques that we learned ages ago. It’s a relief, honestly. No more wrestling with confusing calculus!
But the story doesn't end there. Once we’ve figured out the solution in this simpler, transformed world, we need to bring it back to reality. And guess what? Laplace has another magic trick up his sleeve: the Inverse Laplace Transform. This is the reverse spell. It takes our neat algebraic solution and poof! It transforms it back into the original, messy differential equation’s solution. We get our robot’s actual movements, its trajectory, its every wiggle and jiggle, all laid out for us.

It's like having a translator who can turn complex jargon into everyday language, and then translate the simple answer back into the original, nuanced context.
Think about it like this: You’re trying to understand a complicated recipe for your grandmother’s famous cookies. It’s written in her old, cryptic handwriting, with smudges and maybe a few forgotten ingredients. It’s a mess! So, you decide to rewrite it in your own, clear handwriting, making each step super simple. You bake the cookies, they turn out amazing! Then, you take your clear, step-by-step instructions and translate them back into a format that perfectly captures the essence of your grandmother’s original (but messy) recipe. You haven't just baked cookies; you've understood the entire legacy!
This whole process is particularly heartwarming when we’re dealing with initial value problems. These problems are like starting a race with a specific starting position. We know where our robot (or our cookie dough, or our falling apple) began. The differential equation tells us how it moves from that starting point, and Laplace Transforms help us figure out exactly where it will end up. It’s about predicting the future based on a starting point and a set of rules. It's like having a crystal ball, but powered by math!

So, the next time you hear about Laplace Transforms, don't get intimidated. Think of it as a brilliant problem-solver, a mathematical magician who can take the most chaotic situations and turn them into solvable puzzles. It’s the unsung hero that helps us understand everything from the gentle swing of a pendulum to the complex vibrations in an engineering structure. It’s a little bit of magic, a lot of cleverness, and a whole lot of fun if you let it be!
It's a reminder that even the most daunting-looking mathematical tools can have elegant, almost whimsical applications. They are not just abstract concepts; they are powerful keys that unlock our understanding of the world around us, making the complex beautifully simple, and then beautifully real again. It's like a grand reveal, a surprise party for our understanding, all thanks to the magic of Laplace.
