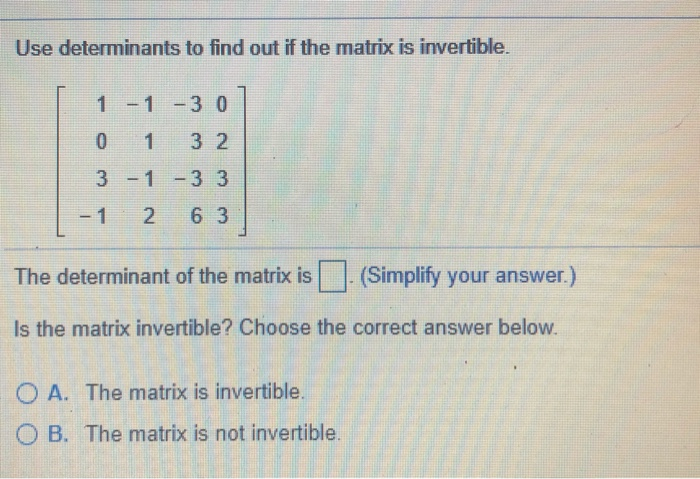
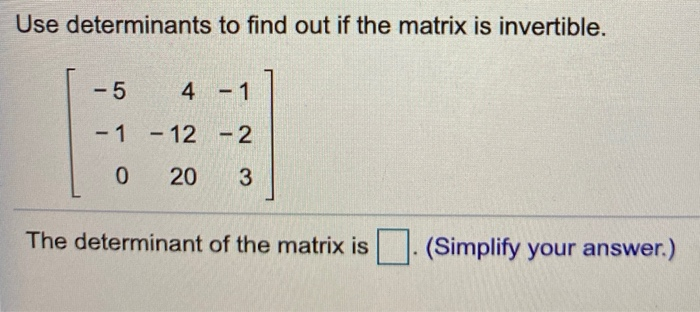
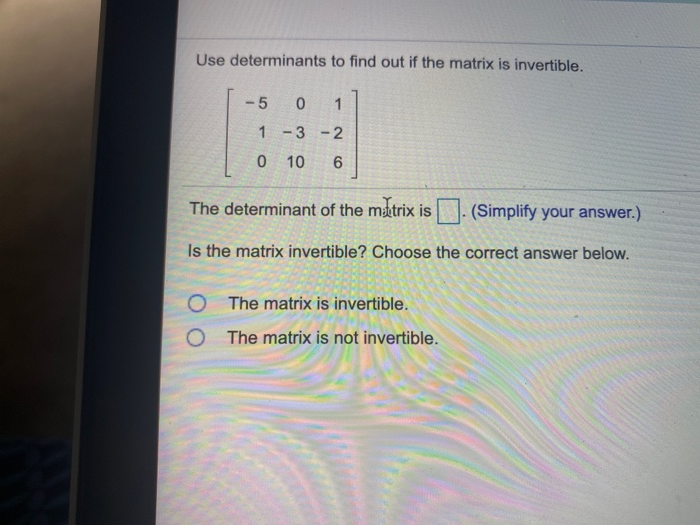
Use Determinants To Find Out If The Matrix Is Invertible
Ever wondered if you can tell if a bunch of numbers arranged in a square can be "flipped" or "inverted"? It sounds a bit like magic, right? Well, there's a super cool trick that lets us peek behind the curtain and know for sure. It's all about a special number called the determinant.
Think of a matrix like a grid of numbers. Sometimes, these grids are special. They have a hidden quality that allows them to be "undone," much like you can undo a button you've fastened. This ability to be undone is what we call invertibility.
So, how do we discover this secret superpower? It's all thanks to the determinant. This isn't just any random number; it's a calculated value that tells us a profound story about the matrix itself. It’s like a secret handshake that only invertible matrices can perform.
Imagine a matrix as a tiny machine. The determinant is like a little meter on that machine. If the meter reads a certain special value, you know the machine is working perfectly and can be reversed. If it reads another value, well, it's stuck and can't be reversed.
The Magic Number: The Determinant
The determinant is calculated using a specific set of rules, depending on the size of the matrix. For a simple 2x2 matrix, it's wonderfully straightforward. You just do a little cross-multiplication and subtraction. Easy peasy!
Let's say you have a matrix like this:
[ a b ]
[ c d ]
The determinant is calculated as (a * d) - (b * c). See? Just a few operations. It’s like a secret recipe!
This number, the determinant, holds the key to invertibility. It’s the ultimate judge, the final arbiter. It tells us if our grid of numbers is "flippable" or not.
So, what's the rule? It's surprisingly simple and elegantly profound. If the determinant of a matrix is not zero, then congratulations! That matrix is invertible. It has that special "undo" button.
But, if the determinant is exactly zero, then the matrix is like a one-way street. It cannot be inverted. It's stuck in its current form, unable to be reversed.
It's a bit like having a special key. If you have the right key (a non-zero determinant), you can unlock the door and go back. If the key is broken or doesn't fit (a zero determinant), the door remains shut.
Why Is This So Cool?
This little calculation makes working with matrices so much more predictable and powerful. Instead of blindly trying to invert a matrix and getting stuck, we can take a quick peek at its determinant first. It saves a lot of time and prevents frustration.
It's like having a spoiler alert for your math problems. You know the outcome before you even start the hard work of inversion. This foresight is incredibly valuable, especially when dealing with larger, more complex matrices.

Think about it: discovering the invertibility of a matrix is like solving a mini-puzzle. The determinant is the final piece that reveals the answer. It’s a moment of clarity, a "eureka!" when you understand the true nature of your number grid.
This concept is a cornerstone in many areas of mathematics and science. From solving systems of equations to understanding transformations in geometry, the idea of invertibility is crucial. And the determinant is our trusty guide.
The beauty lies in its universality. Whether you have a 2x2 matrix or a massive 100x100 one, the principle remains the same. A non-zero determinant means invertibility; a zero determinant means no luck.
The Thrill of Discovery
There's a certain thrill in using the determinant to make this discovery. It feels like you've unlocked a secret code. You’re not just crunching numbers; you’re understanding a fundamental property of the mathematical object you’re working with.
It's a little like being a detective. The matrix is your suspect, and the determinant is your clue. That single number tells you if your suspect has a hidden past that can be uncovered or if they’re a straightforward character.

And as matrices get bigger, the calculation of the determinant itself becomes a more involved process, often requiring clever shortcuts and techniques. This adds another layer of challenge and reward to the whole endeavor.
But even with more complex calculations, the core idea stays the same: find the determinant, and you'll know if you can invert. It’s a powerful, elegant, and surprisingly satisfying mathematical tool.
So next time you encounter a matrix, don't just stare at it. Remember the determinant! It’s your ticket to understanding if that grid of numbers has the fascinating ability to be inverted. It’s a simple check with profound implications, and it makes the world of matrices just a little bit more magical.
It's a fundamental concept that unlocks further exploration. Once you know a matrix is invertible, you can then proceed to find its inverse, which opens up a whole new world of problem-solving possibilities. The determinant is the gatekeeper to all of that.
The elegance of mathematics is often found in these simple yet powerful tools. The determinant is a prime example. It distills complex information about a matrix into a single, easily interpretable number.
It's amazing how much information can be packed into one value. The determinant doesn't just tell you about invertibility; it also reveals things about the matrix's rank and its eigenvalues, but that's a story for another day! For now, knowing it tells you about invertibility is a fantastic starting point.
So, embrace the determinant. It's your friend, your guide, and your secret weapon in navigating the fascinating landscape of linear algebra. Give it a try, and you might just find yourself enjoying the process of uncovering a matrix's invertible nature.
It’s a bit like knowing if a lock has a key. The determinant is the key, and if it’s there (non-zero), you can unlock the matrix’s inverse. If it's not (zero), then that particular lock is unpickable, at least in the invertible sense.
The journey through matrices can be daunting, but tools like the determinant simplify things greatly. They provide clarity and confidence, allowing you to tackle more advanced concepts with a solid foundation. This one little number makes a world of difference.
So go ahead, calculate a determinant. See if your matrix is ready to be flipped. It's a simple step that opens up a universe of mathematical possibilities. You might be surprised at how enjoyable this discovery process can be!
