Unit 7 Polygons & Quadrilaterals Homework 2 Parallelograms

Hey there, geometry whiz (or soon-to-be whiz)! So, we're diving headfirst into Unit 7, and guess what? It's all about those cool, straight-sided shapes: polygons! And today, we’re zooming in on a particularly awesome bunch of them – the parallelograms. Think of them as the VIPs of the quadrilateral world. Seriously, they've got some pretty sweet deals going on.

Now, I know what you might be thinking: "Homework 2? Parallelograms? Is this going to be as exciting as watching paint dry?" Well, hold your horses! We're going to make this as painless, and dare I say, fun, as possible. Think of this as our little chat about why these shapes are so neat, and how to nail that homework assignment without breaking a sweat. After all, who needs math stress when you can have math success?

So, What Exactly IS a Parallelogram?

Alright, let's break it down. A parallelogram is a special type of quadrilateral. Remember, quadrilaterals are just fancy talk for any shape with four sides. So, squares, rectangles, rhombuses, and even those slightly wonky trapezoids – they're all quadrilaterals. But a parallelogram is like the coolest kid in that quadrilateral club.

What makes it so special? It’s all about those parallel sides. That's where the name "parallelogram" comes from, get it? Parallel-o-gram! So, a parallelogram is a quadrilateral where both pairs of opposite sides are parallel. Imagine two train tracks running side-by-side – they never meet, right? That's parallel! In a parallelogram, you've got two sets of these "train tracks" that are perfectly parallel to each other.

This little detail unlocks a whole bunch of cool properties. It’s like getting a secret handshake that opens up all sorts of geometric doors. Pretty neat, huh?

The "Aha!" Properties of Parallelograms

This is where the magic happens. Because those opposite sides are parallel, some really neat things automatically become true for all parallelograms. You don't even have to prove them; they just are. It's like discovering free Wi-Fi – a wonderful surprise!

Property 1: Opposite Sides are Congruent (Equal Length!)

This is a biggie. If you have a parallelogram, then the opposite sides are not only parallel, but they're also the same length. So, if one side is 5 inches long, the opposite side is also 5 inches long. If the other side is 8 inches long, its opposite buddy is also 8 inches long. No more measuring guessing games!

Think about it: if the sides were different lengths, they'd eventually have to "lean in" or "lean out" and wouldn't be able to stay parallel. It just makes sense, doesn't it? It’s like having a perfectly balanced scale. Both sides match!

Property 2: Opposite Angles are Congruent (Equal Measure!)

Now let's talk angles. You know, those pointy bits where the sides meet. In a parallelogram, the opposite angles are also equal. So, if one corner is a sprightly 70 degrees, the corner directly across from it is also a cool 70 degrees. And if another corner is a more laid-back 110 degrees, its opposite twin is also 110 degrees.

Why does this happen? Well, remember those parallel lines? When you have a line (a side of the parallelogram) cutting across two parallel lines, you get some special angle relationships. It's a bit like a geometric domino effect. And voilà! Opposite angles end up being identical. It's like they went to the same angle school and got the same diploma.

Property 3: Consecutive Angles are Supplementary (Add Up to 180°!)

Okay, "supplementary" sounds a bit serious, but it just means they add up to 180 degrees. Consecutive angles are the angles that are next to each other, sharing a side. So, in our parallelogram, if you take one angle and add the angle right next to it, you'll always get 180 degrees. Think of it as two angles making a perfect straight line.

This property is directly linked to the opposite angles being equal. Remember those parallel train tracks? When a side cuts across them, the angles on the same side of the cut (our consecutive angles) are supplementary. It’s a really handy property for figuring out missing angles. If you know one, you can figure out all the rest! It’s like having a secret shortcut to knowledge.

Property 4: Diagonals Bisect Each Other (They Cut Each Other in Half!)

Now for the diagonals. A diagonal is just a line segment that connects two opposite corners of a polygon. In a parallelogram, if you draw both diagonals, they'll cross each other right in the middle. And the coolest part? They cut each other exactly in half. The point where they intersect is the midpoint for both diagonals.

So, if one diagonal is 10 inches long, when it gets cut in half by the other diagonal, you'll have two 5-inch pieces. It’s like the diagonals are saying, "Hey, let's share this intersection point fairly." This is a super useful property for solving problems where you're given the lengths of the diagonal pieces.

Putting It All Together: Your Homework Mission, Should You Choose to Accept It...

So, your "Unit 7 Homework 2: Parallelograms" is probably going to test your understanding of these properties. You might get problems that look like this:

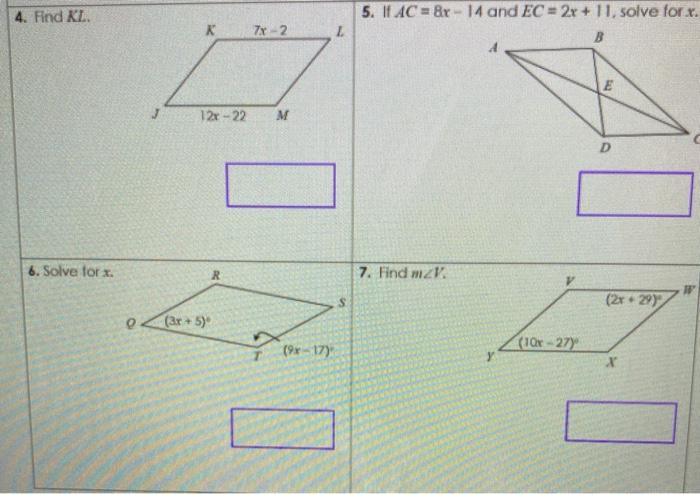
• "Given a parallelogram with sides of length 7 cm and 12 cm, what are the lengths of the other two sides?" (Hint: Property 1!)
• "One angle in a parallelogram measures 85 degrees. What are the measures of the other three angles?" (Hint: Properties 2 and 3!)
• "The diagonals of a parallelogram intersect at point M. If AM = 6 inches and BM = 4 inches, what are the lengths of the diagonals AC and BD?" (Hint: Property 4! Remember, M is the midpoint of both.)
• "Prove that a quadrilateral with opposite sides parallel is a parallelogram." (Okay, maybe not that one for this homework, but it's the foundational definition!)

Don't be intimidated! Just remember these four key properties, and you'll be golden. Think of them as your superhero toolkit for solving parallelogram puzzles.

Special Types of Parallelograms (The A-Listers!)

Now, while all parallelograms are cool, some are like the super-famous celebrities of the geometric world. These are shapes that are also parallelograms, but they have even more special properties. You've probably heard of them!

The Rectangle: The "All Right Angles" Guy

A rectangle is a parallelogram where all four angles are right angles (90 degrees). So, it’s got all the parallelogram properties (opposite sides parallel and equal, opposite angles equal, consecutive angles supplementary, diagonals bisect each other), PLUS all its angles are equal. Imagine a perfectly squarish-looking shape, but it can be stretched longer.

The diagonals of a rectangle are also congruent (equal in length) to each other. This is a special bonus that not all parallelograms have! So, if you hear "rectangle," think "parallelogram with 90-degree corners and equal diagonals."

The Rhombus: The "All Sides Equal" Diva

A rhombus is a parallelogram where all four sides are the same length. It’s like a diamond shape. It's got all the parallelogram properties, PLUS all its sides are equal. Think of a tilted square.

The diagonals of a rhombus have their own cool trick: they bisect the angles. This means each diagonal cuts its corner angles exactly in half. Also, the diagonals of a rhombus are perpendicular (they meet at a 90-degree angle). This is another bonus property!

The Square: The Ultimate Superstar!

And then, the king of the hill, the grand champion – the square! A square is a shape that is both a rectangle and a rhombus. This means it has all the properties of a parallelogram, plus all the special properties of rectangles and rhombuses.

So, a square has:

• Opposite sides parallel and equal (Parallelogram)
• All angles are right angles (Rectangle)
• All sides are equal length (Rhombus)
• Diagonals bisect each other (Parallelogram)
• Diagonals are congruent (Rectangle)
• Diagonals are perpendicular (Rhombus)
• Diagonals bisect the angles (Rhombus)

Wowza! That's a lot of awesome packed into one shape. It’s like the Swiss Army knife of quadrilaterals.

Don't worry too much about these special types just yet if your homework is purely about general parallelograms. But it's good to know they exist and are part of the parallelogram family tree! They just took their parallelogram education to the next level.

Tips for Conquering Your Homework

Okay, so let's get practical. When you're tackling those homework problems, here's how to stay calm and collected:

1. Draw a Picture! Seriously, this is your best friend. Even if the problem gives you a diagram, sketching your own parallelogram and labeling the sides and angles can make a huge difference. And don't worry about making it perfectly to scale; just make it look like a parallelogram.
2. Identify the Properties Being Used. As you read each problem, ask yourself: "Is this problem about sides? Angles? Diagonals?" This will help you remember which property to apply.
3. Label Everything. If you're given values, write them on your drawing. If you need to find a value, label that with a variable (like 'x'). It makes the problem less abstract.
4. Don't Be Afraid to Go Back to Basics. If you're stuck, just reread the definitions and properties. They're your cheat sheet!
5. Practice Makes... Well, Not Perfect, but Pretty Darn Good! The more problems you do, the more natural these properties will feel. It’s like learning to ride a bike; you might wobble at first, but soon you'll be cruising.

And remember, it's okay to make mistakes! Mistakes are just opportunities to learn something new. Think of them as little detours on the road to understanding. They're not failures; they're just part of the process.

You've Got This!

So there you have it! Parallelograms. They're not scary monsters; they're just fascinating shapes with a predictable set of rules. By understanding their parallel sides, congruent opposite sides and angles, supplementary consecutive angles, and bisecting diagonals, you're well on your way to acing this homework.

Think of it this way: you're not just doing homework; you're becoming a geometry detective, uncovering the secrets of these perfectly balanced shapes. Each problem you solve is a little victory, a testament to your sharp mind and your growing geometric prowess. So go forth, embrace the parallelograms, and show that homework who's boss! You’ve got the brains, you’ve got the tools, and you’ve definitely got this. Happy problem-solving!