Unit 4 Lesson 7 Right Triangles And Trigonometry Unit Test
You know, the other day I was trying to assemble this ridiculously complicated bookshelf. The instructions, bless their hearts, were basically a series of hieroglyphs and vague arrows. At one point, I was staring at two pieces of wood, totally convinced they had to connect at a perfect 90-degree angle, but something was off. It was like trying to fit a square peg in a slightly-less-square hole, but with splinters. I swear, for a solid ten minutes, my entire world revolved around achieving that elusive right angle. It got me thinking, how often do we actually rely on those perfect, clean 90-degree corners in our lives? And more importantly, how do we measure them when things aren't quite so… manufactured?
Turns out, the answer, my friends, is all about a magical world called trigonometry, specifically within the realm of right triangles. Yeah, I know, the word itself sounds like something a wizard would mutter before conjuring a spell. But stick with me, because Unit 4 Lesson 7, the one that culminates in the dreaded (or perhaps, exhilarating, depending on your mood) Unit Test on Right Triangles and Trigonometry, is actually pretty darn cool once you get past the initial intimidation. Think of it as the secret handshake for understanding angles and distances in a way that's way more practical than just eyeballing it with your bookshelf pieces.
So, what’s the big deal with right triangles? Well, they’re the foundation of so much. Imagine you're a builder, trying to make sure your walls are perfectly upright. Or a sailor, navigating by the stars. Or even a gamer, trying to calculate the trajectory of a virtual projectile. All of these scenarios, and a million more, boil down to understanding the relationships between the sides and angles of a right triangle. It's the most basic, yet most powerful, geometric shape in the universe, if you ask me. And the Unit 4 Lesson 7 Unit Test? That’s your chance to show off how well you’ve mastered its secrets.
Let's break it down a bit. The star of the show, of course, is the right angle. That perfectly square corner, the one that makes everything feel stable and correct. In a right triangle, this angle is always 90 degrees. You can spot it easily – it’s the one that looks like the corner of a book, or, you know, a perfectly constructed bookshelf piece. The sides that form this angle are called the legs, and the longest side, the one opposite the right angle, is the hypotenuse. Ever heard of the Pythagorean theorem? That’s all about the relationship between these three sides: a² + b² = c², where 'a' and 'b' are the lengths of the legs, and 'c' is the length of the hypotenuse. If you aced that part, you’re already halfway there to conquering the test!
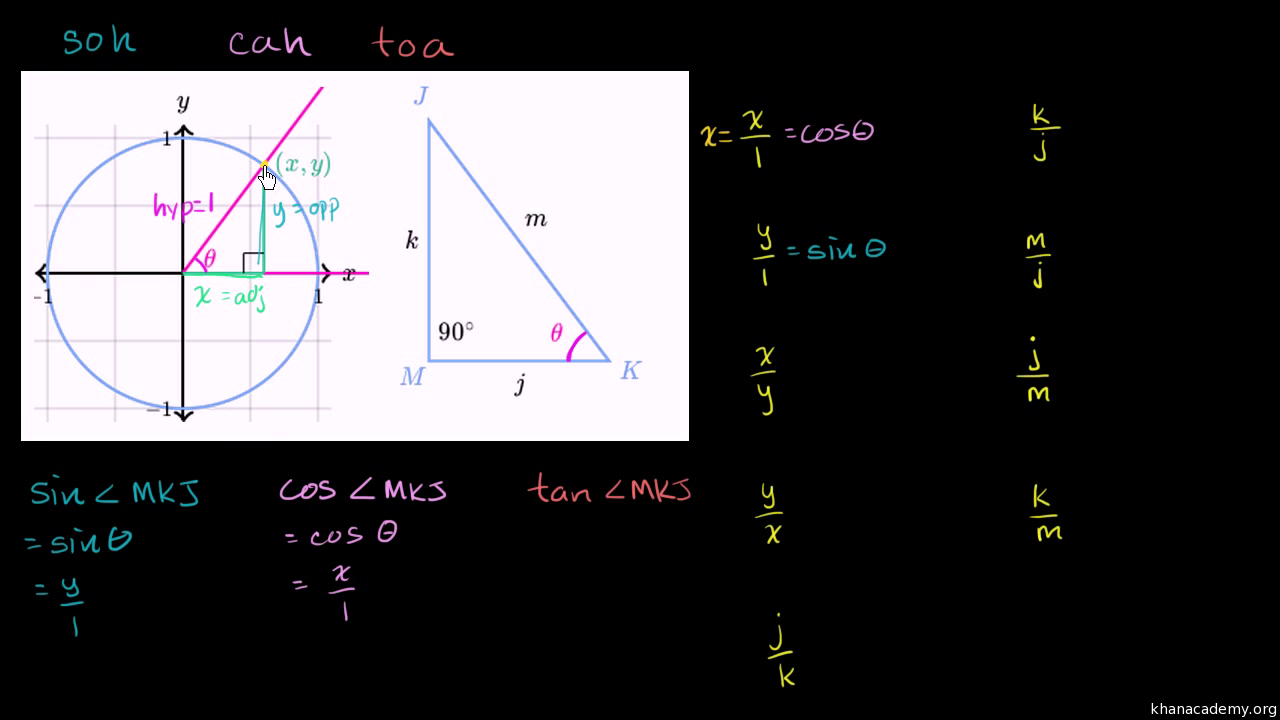
But the real magic, the stuff that really makes your brain do a little jig of understanding, comes in when we start talking about trigonometry. Now, this isn't about using a protractor for everything. Trigonometry gives us a way to relate the angles inside a right triangle to the ratios of its sides. It’s like having a universal translator for angles and distances. The three amigos of trigonometry are sine (sin), cosine (cos), and tangent (tan). Don't worry if these names sound a bit foreign; they're just fancy ways of describing specific ratios.

Think of it this way: if you have a right triangle, and you pick one of the other angles (the non-right ones, remember?), you can define these trigonometric functions based on that angle. The sine of an angle is the ratio of the opposite side to the hypotenuse. The cosine is the ratio of the adjacent side (the one next to the angle, but not the hypotenuse) to the hypotenuse. And the tangent? That’s the ratio of the opposite side to the adjacent side. See? It's all about comparing the lengths of the sides based on which angle you're focusing on.
This is where things get seriously useful. Let's go back to that bookshelf. If I knew the angle of one of the pieces I was trying to fit, and I knew the length of one of the sides, I could use trigonometry to calculate the exact length of the other side needed to make that perfect 90-degree corner. No more guessing, no more wobbly furniture! The Unit 4 Lesson 7 Unit Test will definitely be throwing some problems at you that require you to apply these ratios. You might be given two sides and asked to find an angle, or given an angle and a side and asked to find another side. It’s all about that SOH CAH TOA mnemonic. Seriously, if you don't have that etched into your brain yet, now's the time. It’s your cheat sheet for life (well, for this test, at least!).
Let's imagine a practical scenario. Suppose you're standing at the base of a really tall building, and you want to know its height. You can't exactly climb up there with a tape measure, can you? (Please don’t try this, it's not safe and definitely not on the test!). But, if you have a way to measure the angle from where you're standing up to the top of the building (let's call this your angle of elevation), and you know how far away you are from the building (the distance on the ground), then BAM! You have a right triangle. The height of the building is the opposite side to your angle of elevation, and your distance from the building is the adjacent side. Which trigonometric function relates opposite and adjacent? That's right, tangent! So, you can calculate the height of the building using a simple tangent ratio. Pretty neat, huh? The Unit Test might throw a similar real-world problem your way, so get comfortable with these applications.

Another aspect that Unit 4 Lesson 7 likely covers is the inverse trigonometric functions, also known as arcsine (sin⁻¹), arccosine (cos⁻¹), and arctangent (tan⁻¹). These are your tools for finding the angle when you know the ratios of the sides. So, if you know the opposite and adjacent sides, you can use arctangent to find the angle. This is super handy when you're trying to figure out the steepness of something, like a hill or a ramp. The Unit 4 Lesson 7 Unit Test will probably have questions where you're given side lengths and need to find the angles. Don't let those little "-1" superscripts freak you out; they just mean you're working backwards.
It’s also worth mentioning the other angles in a right triangle. Since the sum of angles in any triangle is always 180 degrees, and one angle is 90 degrees, the other two acute angles (angles less than 90 degrees) must add up to exactly 90 degrees. This is a crucial piece of information. If you know one of the acute angles, you automatically know the other one. This can simplify some problems on the Unit 4 Lesson 7 Unit Test, so keep it in the back of your mind. Sometimes the solution is staring you right in the face!

Now, let's talk about what you might actually see on the Unit 4 Lesson 7 Right Triangles and Trigonometry Unit Test. Expect a mix of things. You'll probably have questions that test your understanding of the Pythagorean theorem – calculating a missing side when you know the other two. Then come the trig ratios: using sine, cosine, and tangent to find missing sides when you have an angle and a side. Conversely, you'll likely have problems where you're given side lengths and have to find the angles using the inverse functions. Word problems are almost a certainty; they’re the teachers’ way of making sure you can apply these concepts beyond just abstract numbers. Think about ladders leaning against walls, shadows cast by objects, or the height of a kite flying in the wind. These are all classic right triangle and trigonometry scenarios.
One tip for tackling the test: draw a diagram! Seriously, for any problem that involves geometry, sketching it out can make a world of difference. Label your sides (opposite, adjacent, hypotenuse) and your angles clearly. This will help you visualize the problem and make sure you're using the correct trigonometric function. Don't be afraid to use your calculator, especially for finding the values of sine, cosine, and tangent, and for their inverse functions. Just make sure it's in degree mode! This is a common trap, and a misplaced button press can send your entire answer spiraling into the wrong dimension. Double-check your calculator settings!
I remember my first trigonometry class. I was convinced it was going to be way over my head. I pictured myself lost in a sea of Greek letters and complex formulas. But as we went through the lessons, especially Unit 4 Lesson 7, and started seeing how it applied to real-world problems, it clicked. It was like suddenly being able to see in a new dimension. The world around me started to look like a giant collection of right triangles, just waiting to be measured and understood. That feeling of understanding, of unlocking a new way to see and interact with the world, is what makes learning these concepts so rewarding.
![[FREE] Unit 7: Right Triangles & Trigonometry Homework 4: Trigonometry](https://media.brainly.com/image/rs:fill/w:1920/q:75/plain/https://us-static.z-dn.net/files/daf/371a7383384b9f267987ef9f8f3ce51f.png)
So, as you prepare for the Unit 4 Lesson 7 Right Triangles and Trigonometry Unit Test, try to shift your perspective. Don't just see it as a hurdle to overcome. See it as an opportunity to gain a powerful new toolset for understanding the world. Think about those situations where precise angles and distances matter. From the smallest microchip to the largest skyscraper, from the flight of a bird to the orbit of a planet, the principles of right triangles and trigonometry are at play. You're not just learning math; you're learning a language of measurement and space.
Don't panic if you’re feeling a little overwhelmed. It's completely normal. Take it one concept at a time. Master the Pythagorean theorem. Understand sine, cosine, and tangent. Practice using your calculator for both direct calculations and inverse functions. Work through as many practice problems as you can. The more you practice, the more comfortable and confident you'll become. And who knows, maybe you'll even start seeing the world in terms of right triangles like I do. You might find yourself looking at a slanted roof and instinctively calculating its pitch, or observing a construction site and mentally checking the angles. It’s a strange but wonderful new way to see!
Ultimately, the Unit 4 Lesson 7 Unit Test is a checkpoint. It’s a chance to solidify your understanding and show what you’ve learned. It’s not about tricking you; it's about assessing your grasp of fundamental concepts that will be building blocks for future math and science endeavors. So, go in there prepared, stay calm, and remember that those right triangles and trigonometric ratios are your friends. They’re tools that can help you solve problems and understand the world around you in a more profound way. And hey, maybe you'll even be able to assemble that bookshelf with a newfound confidence. Good luck!
