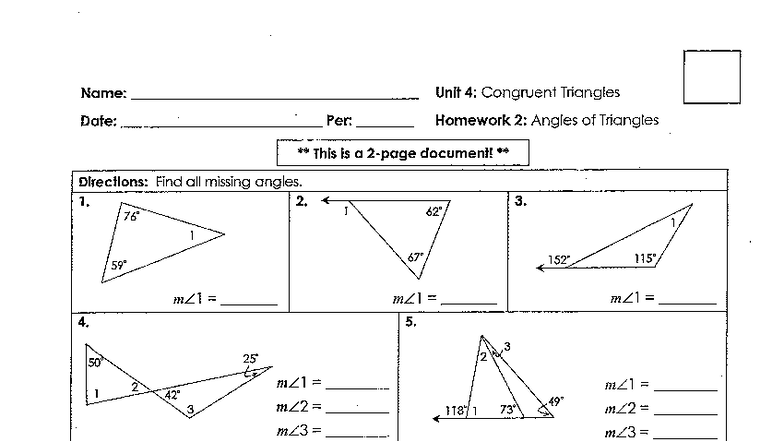
Unit 4 Congruent Triangles Homework 7 Proofs Review All Methods
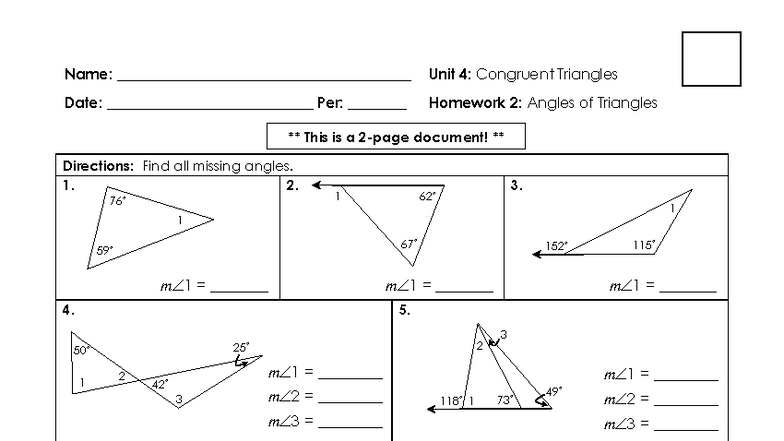
Alright, gather 'round, folks, and let's talk about something that might sound drier than a week-old scone: proofs. Specifically, Unit 4 Congruent Triangles Homework 7 Proofs Review All Methods. Yeah, I know, it's not exactly a thrilling plotline for your next Netflix binge. But trust me, after this, you'll be looking at triangles with a whole new appreciation. Think of it as the secret lives of geometric shapes, and we're about to spill all the tea.
So, you've been wrestling with these proofs, right? Maybe you've stared at them until your eyes felt like they were about to stage a jailbreak from your head. Perhaps you've even muttered sweet, nonsensical things to your geometry textbook, begging it to reveal its secrets. Been there. Done that. Wore the slightly-too-small "I Survived Congruent Triangles" t-shirt (it was a gag gift, okay?).
The whole point of congruent triangles is basically figuring out if two triangles are exactly the same. Like twins, but with straighter lines and fewer questionable fashion choices. And how do we prove they're the same? Not by asking them nicely, or sending them on a DNA test (though I've seriously considered that for some homework problems). We use these magical little shortcuts, these superpowers of geometry. Today, we're dusting off the instruction manual for these superpowers.
The Usual Suspects: SSS, SAS, ASA, AAS
First up, let's talk about the OG squad, the heavy hitters. These are the basic postulates that make proving triangles congruent feel almost... dare I say... easy? We're talking about:
SSS (Side-Side-Side)
This one's a real crowd-pleaser. If you can show that all three sides of one triangle are equal in length to the corresponding three sides of another triangle, then BAM! They're congruent. It's like saying, "Look, they're identical triplets down to the last millimeter!" No trickery, no illusions. Just pure, unadulterated side-to-side sameness. It's so straightforward, it almost feels too easy. You're probably thinking, "Is that it?" Yep, that's it. Mind-blowing, I know. My mind was blown the first time, and I've been working with these things for years. I think I still owe my brain a thank-you note for not exploding.
SAS (Side-Angle-Side)
Now, this one's a bit more discerning. It’s not just any angle and any two sides. The angle has to be sandwiched between the two sides. Think of it like a perfect sandwich. You’ve got your bread (the sides), and the delicious filling (the angle) right in the middle. If you have two sides and the angle between them that are equal in both triangles, they’re congruent. If the angle is on the outside, it's like putting the lettuce on the outside of the sandwich. It’s just… wrong. And it won't prove congruence. So, remember: included angle is key. It’s the culinary secret of geometry!
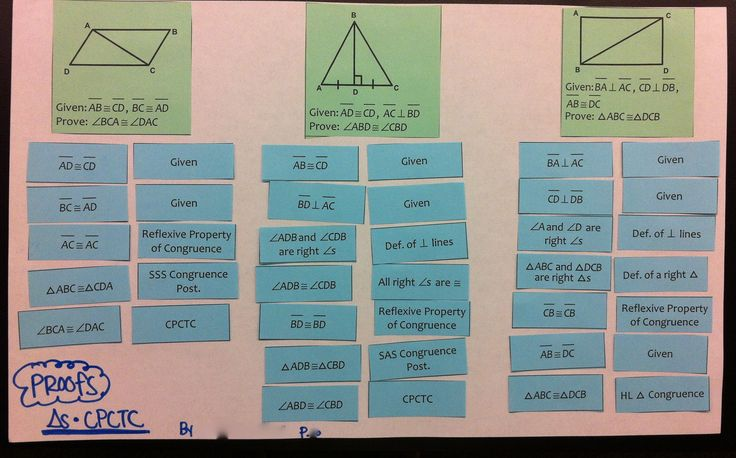
ASA (Angle-Side-Angle)
This is SAS's slightly more angled cousin. Here, we're looking for two angles and the side between them. So, you've got an angle, then the side connecting those two angles, and then another angle. Like two people holding hands, with a nice, sturdy fence between them. If these three elements match up in both triangles, you’re golden. This is where you can really start to feel like a geometric detective, piecing together clues. It’s like solving a tiny, two-dimensional mystery, and you’re the one with the magnifying glass.
AAS (Angle-Angle-Side)
This one’s a bit of a rebel. It's like SAS and ASA decided to spice things up. Here, the side isn't between the two angles. It's outside of them. So you've got an angle, then another angle, and then a side that's off to the side. Think of it as the "surprise side." You didn't expect it, but it's there, and it’s crucial! This is a lifesaver when you can't quite get that included side. It’s the geometric equivalent of finding a twenty-dollar bill in an old coat pocket – a happy accident that proves your point.
The MVP: HL (Hypotenuse-Leg)
Now, for a special shout-out to the absolute MVP of triangle congruence: HL. This one only applies to right triangles, so don't go trying to use it on your average, everyday triangles unless you want a geometric facepalm. If you have two right triangles, and their hypotenuses are equal, and one pair of corresponding legs are equal, then those triangles are congruent. This is like having a VIP pass. It's so powerful, it can bypass some of the other requirements. It’s the ninja move of triangle proofs. Imagine your triangles are superheroes. HL is the one with the laser eyes and the super-strength. They're unstoppable!

Why is HL so special? Well, if you think about it, in a right triangle, the Pythagorean theorem (a² + b² = c²) is always lurking. So, if you know the hypotenuse (c) and one leg (say, a), you can always figure out the other leg (b). This means that knowing the hypotenuse and one leg is basically like knowing two legs! That's why HL is so darn efficient. It's like a shortcut that knows all the other shortcuts. It’s basically cheating, but in a totally acceptable, mathematically brilliant way. I'm pretty sure Pythagoras high-fived himself when he figured this one out.
The Art of the Proof: Beyond the Acronyms
So, you've got your tools. Now what? Proofs are basically a step-by-step argument, like building a case in a courtroom, but for triangles. You start with what you know (the givens), and you use your geometric rules (like the postulates we just discussed, or even definitions and other theorems) to logically connect those givens to what you want to prove. It’s a beautiful dance of logic and geometry. And sometimes, it feels like you’re trying to herd a flock of very stubborn cats.
A typical proof will have two columns: one for your statements (what you're claiming) and one for your reasons (why your claim is true). For example:
Statement: AB ≅ DE Reason: Given
Then you keep going, building your case. You might use the fact that vertical angles are congruent, or that an angle bisector creates two equal angles. The possibilities are endless, which is both exciting and, let's be honest, sometimes a little terrifying. It’s like having a buffet of logical choices, and you have to pick the perfect combination.
The trick is to always have a "why." Don't just say two things are equal. Say why they're equal. And make sure your "why" is a valid geometric reason. No "because I said so" allowed in the hallowed halls of geometry. That's a one-way ticket to a "needs more work" comment from your teacher. And nobody wants that. We're aiming for "chef's kiss" proofs here.

The "Wait, What?" Moments and How to Conquer Them
Sometimes, you'll get a problem where you need to draw an auxiliary line. This is like adding a secret weapon to your arsenal. It's a line you draw yourself, usually to create new triangles or angles that will help you prove congruence. It's like adding a crucial plot twist to your story. The trick is to draw it strategically. Think like a chess grandmaster; every move should have a purpose. Often, these auxiliary lines will help you use the SSS, SAS, ASA, or AAS postulates, or even HL if you’re lucky.
And then there are the proofs that seem to go in circles. You feel like you're running on a treadmill, getting nowhere fast. This is usually a sign that you need to look at the problem from a different angle. Perhaps you need to prove something else first before you can prove the triangles themselves are congruent. It's like needing to find the key to a locked door before you can enter the room. Don't be afraid to backtrack and re-evaluate your strategy. Sometimes, the shortest path isn't a straight line; it’s a winding, logical journey.
So, there you have it. Unit 4 Congruent Triangles Homework 7 Proofs Review All Methods. It's not just about memorizing acronyms; it's about understanding the logic, the strategy, and the sheer elegance of geometric proofs. Go forth, brave geometric warriors, and conquer those triangles! May your statements be true and your reasons be ever so valid. And if all else fails, just remember: triangles are just triangles, and proofs are just fancy ways of showing they're identical twins. Now, who's ready for a coffee break?
