Unit 12 Probability Homework 1 Intro To Sets Venn Diagrams

Alright folks, gather 'round, grab your (imaginary) lattes, and let's talk about something that sounds about as exciting as watching paint dry but is actually, dare I say, kind of fun. We're diving headfirst into the glamorous world of Unit 12 Probability Homework 1: Intro to Sets and Venn Diagrams. Now, I know what you're thinking, "Sets? Venn Diagrams? Is this math or did my cat walk across a keyboard and decide to write a syllabus?" But stick with me, because this is where we learn to organize the glorious chaos of probability. Think of it as giving your probabilities a nice little postcode so they don't get lost on the way to the correct answer.
First off, let's get our bearings. What is probability, anyway? It's basically the mathematical way of saying, "How likely is it that this thing will happen?" Will it rain tomorrow? Will your favorite team win? Will you find that missing sock from the dryer? These are all probability questions. And Unit 12 is our introductory course on how to think about these possibilities in a structured way. It’s like learning the rules of the game before you start betting your life savings on a coin flip. (Please don't actually do that. Unless the coin is really shiny.)
So, we begin with Sets. Don't let the fancy name scare you. A set is simply a collection of distinct objects. Think of it as a very organized junk drawer. You can have a set of your favorite snacks (chips, cookies, that questionable leftover pizza). You can have a set of superhero action figures. Or, in the thrilling world of probability, you can have a set of all possible outcomes when you roll a die. That would be {1, 2, 3, 4, 5, 6}. See? Not so scary. It's just a list. A very important, mathematically sound list.
Now, imagine you have two of these organized junk drawers. Maybe one has your favorite movie genres (Sci-Fi, Comedy, Action) and another has your favorite musical artists (Rock, Pop, Jazz). This is where things get interesting. We can start comparing these sets. We can ask ourselves: What genres do I like and what artists do I like? Or, what genres do I like or what artists do I like?
This is where our star of the show, the Venn Diagram, waltzes in. Imagine a friendly cartoon owl. This owl has two big, round, slightly overlapping glasses. Those glasses? Those are your sets. The Venn diagram is a visual representation that helps us see the relationships between these sets. It's like a magical map for our probability data.
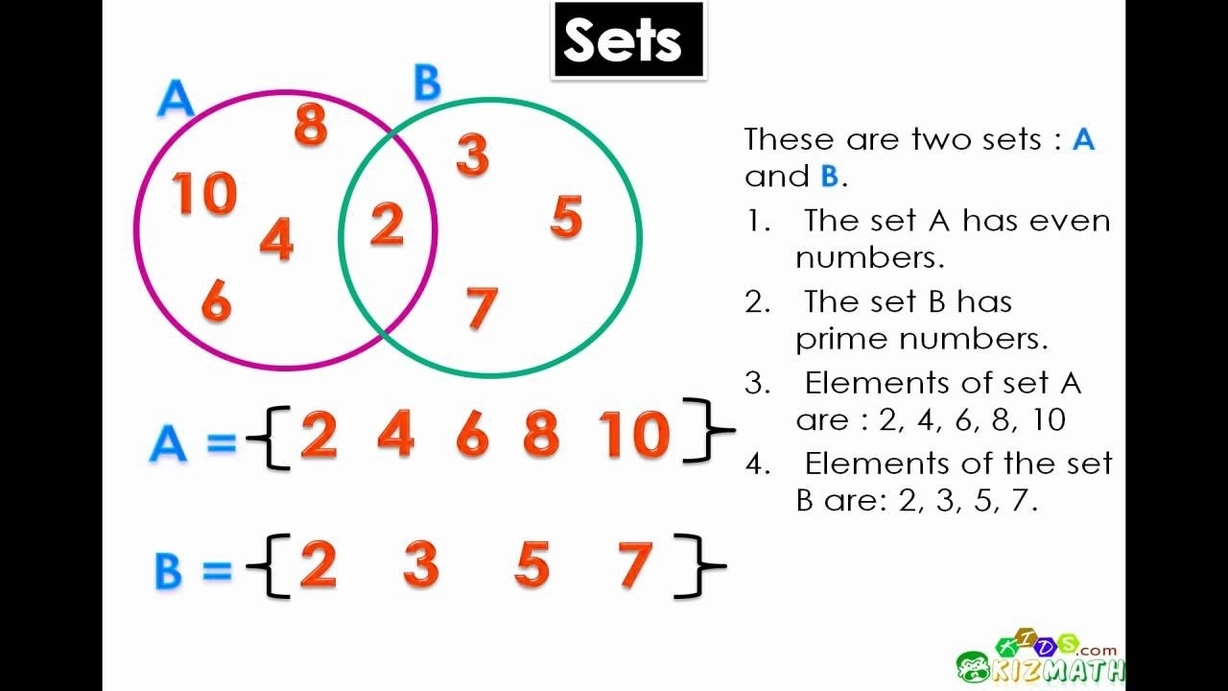
Let’s take our movie genre and music artist example. We draw two big circles. One circle represents "Favorite Movie Genres," and the other represents "Favorite Musical Artists." The magic happens in the overlap. The space where the two circles intersect represents the things that are in both sets. This is called the intersection of the two sets. So, if you love Sci-Fi movies and you also love Rock music, that sweet spot in the middle is where your Sci-Fi and Rock fandoms have their secret rendezvous. It's a beautiful thing, really.
The Intersection: Where Worlds Collide (For Real This Time)
The intersection is denoted by a fancy little symbol that looks like an upside-down 'U'. It's like a tiny mathematical handshake. So, if set A is your favorite movies and set B is your favorite music, A ∩ B (read as "A intersect B") would be the things you love in both categories. It’s the common ground, the shared love, the reason why you always have a killer soundtrack for your space opera marathons.
Now, what about everything that's in either of your circles, or both? That's the union. Think of it as throwing a big party and inviting everyone from both your movie-loving friends and your music-loving friends. Everyone is welcome! In Venn diagram terms, the union is represented by a symbol that looks like a regular 'U'. So, A ∪ B (read as "A union B") includes everything in set A, everything in set B, and everything in their overlap. It's the grand fiesta of your preferences!
Why is this important for probability? Because when we're calculating probabilities, we often need to know the likelihood of event A happening or event B happening, or event A happening and event B happening. The Venn diagram gives us a crystal-clear picture of these possibilities. It helps us avoid double-counting and ensures we're looking at the right slice of the probability pie.

Let's get a bit more mathematical, shall we? Imagine you're surveying your friends about their favorite ice cream flavors. Let's say set 'V' is everyone who likes vanilla, and set 'C' is everyone who likes chocolate. If you have 20 friends, and 10 like vanilla, 12 like chocolate, and 5 like both vanilla and chocolate, how many friends like either vanilla or chocolate? This is where our Venn diagram comes in handy!
We draw two overlapping circles. The overlap (V ∩ C) is 5. Then, for the vanilla-only people, it's 10 (total vanilla) - 5 (both) = 5. For the chocolate-only people, it's 12 (total chocolate) - 5 (both) = 7. So, the total number of friends who like vanilla OR chocolate (V ∪ C) is 5 (vanilla only) + 7 (chocolate only) + 5 (both) = 17. See? It's like a delicious ice cream logic puzzle!
What if some of your friends hate ice cream? (Sacrilege, I know, but for the sake of probability, we must consider all possibilities!) These are the folks who are outside of both the vanilla and chocolate circles. In probability terms, this entire group of all possible outcomes is called the sample space. And the people who don't like vanilla or chocolate are part of the sample space but not in the union of our two sets. We call this the complement. It’s everything else in the universe of our survey.

Think of the sample space as the entire universe. Sets are like galaxies within that universe. Venn diagrams are like super-telescopes that let us zoom in on how these galaxies interact. And the intersection? That's where the wormholes connect them!
So, for homework assignment 1, you'll be dealing with these concepts. You'll be defining sets, drawing Venn diagrams, and identifying intersections and unions. It's all about making sense of possibilities. It’s about building a framework so that when you’re faced with a complex probability problem, you don’t just throw your hands up and say, "The universe is too chaotic!" Instead, you’ll be able to draw a nice, neat Venn diagram and say, "Ah, I see! The probability of that happening is… well, let's calculate it!"
And remember, the more you practice, the more intuitive this becomes. Soon, you’ll be spotting intersections and unions like a hawk spotting a delicious, statistically-likely mouse. It’s a superpower, really. The superpower of organized probability. So go forth, tackle those sets, draw those diagrams, and may your probability calculations be ever in your favor!
