Unit 10 Circles Homework 2 Central Angles & Arc Measures

Okay, so picture this: I was at this ridiculously fancy (and let's be honest, a little intimidating) art gallery opening the other week. The kind with tiny little appetizers that cost more than my weekly grocery bill and people who seem to speak an entirely different language. Anyway, I was trying to look sophisticated, sipping on something bubbly that tasted suspiciously like regret, when I noticed this huge, abstract sculpture. It was basically a giant circle, or at least, a very, very big part of one, with all these weird, jagged bits sticking out. The artist was nearby, looking all profound, so I decided to try and impress him (spoiler alert: I didn't). I pointed at the sculpture and, trying to sound smart, I blurted out, "Wow, that's a really… central piece, isn't it? And look at the… arc it's making!"
He just blinked at me. Then he said, very slowly, "It's… a sculpture." And then he drifted away. Smooth, right? Clearly, my art appreciation needs a serious upgrade. But it got me thinking, even in my awkward attempt at intellectualism, about those words: central and arc. They sound so… mathematical, don't they? And guess what? They absolutely are. Especially when we're talking about our friend, the circle.
So, for anyone else who's ever felt a tiny bit lost when math class starts throwing around words like "central angle" and "arc measure," welcome to the club! This is your friendly, no-judgment zone. Think of this as less of a lecture and more of a casual chat over coffee (or, you know, whatever your beverage of choice is). We’re diving headfirst into Unit 10, Homework 2, all about those nifty little concepts: Central Angles & Arc Measures.
The Heart of the Matter: Central Angles
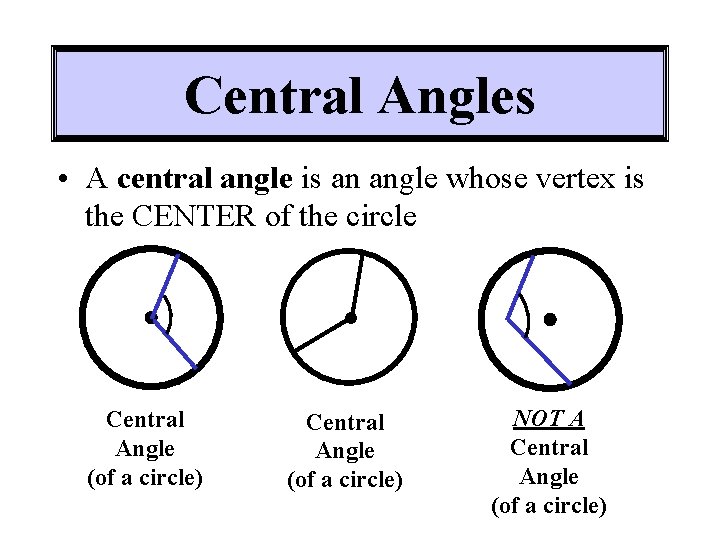
Let's start with the “central” part. What’s in the center of a circle? Yep, you guessed it: the center! So, a central angle is pretty much exactly what it sounds like. It’s an angle whose vertex – that’s the pointy bit where the two lines meet – is located right smack-dab at the center of the circle. The two sides of the angle are then radii of the circle. Think of it like slicing a pizza. The point of the knife where you start cutting is the center, and the two cuts you make to get a slice? Those are the radii forming your central angle.
Why is this important? Because this angle is going to be our key to understanding other parts of the circle. It’s like the captain of the ship, dictating what’s happening around it. Imagine a clock. The hands of the clock originate from the center. The angle between the hour and minute hand? That’s a central angle!
Now, here's a cool little secret that makes things so much easier: the measure of a central angle is equal to the measure of its intercepted arc. Mind. Blown. Well, maybe not blown, but definitely a handy-dandy shortcut.
Following the Curves: Arc Measures
So, what’s an arc? An arc is just a portion or a segment of the circle’s circumference. It’s that curved edge between two points on the circle. Think of that pizza slice again. The crusty, curved part of that slice? That’s the arc.
There are a few types of arcs, but the ones we're most concerned with when we talk about central angles are the ones directly "cut" by the angle. These are often called the minor arc (the shorter path between two points) and the major arc (the longer path). If the central angle is less than 180 degrees, it “intercepts” a minor arc. If it’s more than 180 degrees, it intercepts a major arc.
The measure of an arc is given in degrees, just like angles. And here's where that awesome relationship comes in: The measure of a central angle is always equal to the measure of its intercepted arc.
Let's say you have a central angle that measures 60 degrees. The arc it cuts off? That arc also measures 60 degrees. If your central angle is 120 degrees, the intercepted arc is 120 degrees. Easy peasy, lemon squeezy, right? (Though I'm still not sure why we say that. Lemons aren't exactly known for being easy to squeeze.)
Putting It All Together: The Homework Dive
Okay, so the homework is probably going to give you a bunch of scenarios where you need to figure out one thing if you know the other. You might be given the central angle and asked for the arc measure, or vice-versa. You might be given a diagram with multiple central angles and arcs and asked to find missing values.
Let’s imagine a typical problem. You’ve got a circle, and at the center, there’s an angle labeled 75°. It's pointing to a section of the circle's edge. What's the measure of the arc that this angle cuts off? Yep, you got it – 75°! Because, remember, central angle = intercepted arc.
Or, maybe you see an arc labeled as 130°. You know this is a minor arc (since it's less than 180°). What's the measure of the central angle that intercepts this arc? Again, it’s the same: 130°.
The Curious Case of the Full Circle
Now, what about the whole circle? A full circle has 360 degrees. So, a central angle that goes all the way around, a full rotation, is 360 degrees. And the arc that it intercepts? The entire circumference? That's also 360 degrees. This is a fundamental concept, but it's super important for problems that involve more than one angle or arc.
For example, if you have a central angle of 90 degrees (a right angle!), it cuts off a 90-degree arc. That's exactly one-quarter of the circle. And 90 degrees is indeed one-quarter of 360 degrees. See? It all fits!
Dealing with Major Arcs
What if you're dealing with a major arc? Let's say you have a minor arc that measures 100 degrees. What's the measure of the major arc that connects the same two endpoints? You know the whole circle is 360 degrees. So, the major arc is just the rest of the circle. You'd calculate it like this: 360° - 100° = 260°.
And the central angle that intercepts this major arc? It would be 260 degrees. This is a reflex angle – an angle greater than 180 degrees. So, just keep that in mind. When you’re asked about an arc and given a diagram, look carefully if it's asking for the minor or major arc. Often, they'll use three letters for a major arc (like arc ABC, where B is a point between A and C along the longer path) to avoid confusion with the minor arc (arc AC).
Beyond the Basics: What Else Might Show Up?
You might encounter problems where you have multiple central angles that add up to form a straight line (180 degrees) or a full circle (360 degrees). This is where those basic addition and subtraction skills we learned ages ago come in handy!
Imagine a diameter. A diameter cuts a circle into two equal halves, called semicircles. Each semicircle is an arc of 180 degrees. And the central angle that intercepts a semicircle is a straight angle, also 180 degrees. So, if you have a central angle that forms a straight line across the circle, you know it's 180 degrees, and the arc it creates is also 180 degrees.

What if you have a circle with several central angles, and you know some of them? For instance, you might have three central angles that together make up a full circle. If you know two of them, say 100° and 120°, you can easily find the third one: 360° - 100° - 120° = 140°. And guess what? The arc intercepted by that third angle is also 140°!
A Little Bit of Logic (and Maybe Some Sneaky Diagrams)
Sometimes, the diagrams might not explicitly label every single angle or arc. This is where you have to put on your detective hat. Look for symbols that indicate things like:
- A straight line (which means 180°).
- A right angle symbol (a little square, meaning 90°).
- Congruent angles or arcs (often indicated by tick marks).
If two central angles are marked as congruent, their intercepted arcs are also congruent. This can be a HUGE clue in solving more complex problems.
And don't forget about complementary and supplementary angles! While these are usually applied to angles themselves, the concept can indirectly help. If two central angles are supplementary, they add up to 180 degrees. This means their intercepted arcs also add up to 180 degrees, forming a semicircle. If they are complementary, they add up to 90 degrees, and their intercepted arcs add up to 90 degrees.
The "Why Do I Need to Know This?" Moment
Okay, I know what some of you might be thinking: "When am I ever going to use this in real life?" Beyond impressing art critics (which, as we established, is a risky move), understanding central angles and arc measures is foundational for a lot of other geometry concepts. It’s like learning your ABCs before you can read a novel.

Think about it:
- Navigation: GPS systems and compasses rely on understanding angles and directions, which have roots in circular measurements.
- Engineering and Design: Architects and engineers use circles and arcs in everything from building bridges to designing car tires.
- Computer Graphics: Creating curves and circular shapes on screens involves calculating angles and arc lengths.
- Astronomy: The movement of celestial bodies is often described using degrees and arcs.
So, while it might seem a bit abstract right now, these concepts are building blocks for understanding the world around you in a more precise way. Plus, mastering them is a pretty satisfying mental workout. You’re basically training your brain to be a super-powered problem-solver!
Final Thoughts (and a Little Encouragement)
Unit 10, Homework 2: Central Angles & Arc Measures. It might sound a bit daunting at first, but once you grasp the core idea – that the central angle and its intercepted arc are equals – the rest falls into place. Don't be afraid to draw diagrams, label everything you can, and break down complex problems into smaller steps.
If you get stuck, go back to the definition. What is a central angle? Where is its vertex? What does it intercept? And remember that relationship: central angle measure = intercepted arc measure. It's your golden ticket!
And if you ever find yourself at a fancy art gallery, awkwardly pointing at a sculpture, just remember your math. Maybe you can casually mention the "elegant parabolic arc" or the "precise radial symmetry" instead of just "central" and "arc." You never know, you might just impress someone! (Or at least feel a little more confident about your vocabulary. I know I will be.)
So, go forth and conquer those circles! You’ve got this. Happy calculating!
