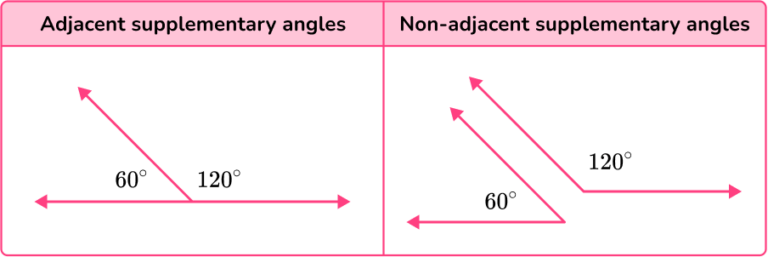
Two Angles Are Supplementary The First Angle Measures 60

Hey there, curious minds! Ever find yourself doodling in a notebook, maybe even while half-listening to a lecture, and your pencil just happens to draw a perfect straight line, and then you split it with another line? Yeah, me too. Sometimes, those little geometric adventures can lead to some surprisingly neat discoveries. Today, we're going to chat about a super chill concept in the world of angles. We're talking about supplementary angles. Sounds fancy, right? But trust me, it's as easy as, well, drawing a straight line and then cutting it.
So, what exactly are these "supplementary" angles? Imagine you've got a perfectly flat, 180-degree surface. Think of it like the horizon on a clear day, or the edge of your breakfast table. That's 180 degrees, a nice, smooth, unbent line. Now, if you take a ray of light, or a superhero's laser beam, and shoot it out from a point on that line, you've just split that 180-degree space into two smaller angles.
And here's the cool part: if those two angles, when you put them back together, form that original 180-degree straight line, they are what we call supplementary. It's like they're perfect puzzle pieces that fit together to make a whole flat surface. Pretty neat, huh?
Now, let's get to the juicy bit. The prompt throws us a little curveball: "Two angles are supplementary. The first angle measures 60 degrees." Okay, so we know they're a pair, destined to make a straight line. We've got one half of the equation. One angle is chilling at a cool 60 degrees. If you picture 60 degrees, it's like a slice of pizza that's a bit less than a quarter, or maybe the angle of your elbow when you're giving a relaxed wave. Not too wide, not too sharp.
So, if one angle is 60 degrees, and its buddy, the supplementary angle, has to complete the 180-degree line with it, what do you think that other angle is? It's like asking, "If I've eaten 60% of a candy bar, and there are only two of us, how much is left for the other person if we want to finish the whole thing?" You'd just subtract 60 from 180, right?
Let's do the math. We know that:
Angle 1 + Angle 2 = 180 degrees
And we're given:
Angle 1 = 60 degrees
So, substituting in:
60 degrees + Angle 2 = 180 degrees

To find Angle 2, we just do a little algebraic magic:
Angle 2 = 180 degrees - 60 degrees
And that gives us:
Angle 2 = 120 degrees

Boom! There it is. The second angle is a whopping 120 degrees. Now, what does 120 degrees look like? Think about that slice of pizza again. If 60 degrees was less than a quarter, 120 degrees is more than a quarter, almost half of the pizza. It's a pretty wide angle. Imagine opening your arms wide, almost like you're about to give a giant hug. That's somewhere in the ballpark of 120 degrees. It's definitely an obtuse angle, meaning it's bigger than 90 degrees.
Isn't it cool how a simple math problem can paint such a clear picture in your mind? We took a number, 60, and by understanding the concept of supplementary angles, we unlocked the value of its partner. It's like cracking a secret code, but the code is geometry!
Why is this even useful, you might ask? Well, beyond just being a fun brain exercise, understanding supplementary angles is foundational for a lot of other geometry concepts. Think about architecture. When architects design buildings, they have to make sure walls meet at specific angles to be stable. Or consider a carpenter cutting wood for a picture frame. If the corners need to be straight, they're dealing with these straight line angles all the time.
It's also like understanding how a ramp works. If a ramp makes a certain angle with the ground, and you want to know the angle it makes with a vertical wall, you might be dealing with supplementary angles. It pops up in unexpected places if you start looking for it!

Let's go back to our pizza analogy for a second. Imagine you're at a party, and the host cuts a giant circular pizza into two equal halves – that's 180 degrees each. But then, maybe they decide to cut one of those halves again. If they make a cut that creates a 60-degree slice from one of the halves, the remaining part of that half has to be 120 degrees. They're still supplementary, adding up to that original 180-degree semi-circle. It's a delicious way to visualize!
Or think about a clock. At 3:00, the hour and minute hands form a perfect 90-degree angle, a right angle. At 6:00, they point in opposite directions, forming a 180-degree straight line. Now, what if it's, say, 2:00? The hour hand is pointing at the '2' and the minute hand at the '12'. The angle between them is 60 degrees (since each number on a clock represents 30 degrees, 12 to 1 is 30, 1 to 2 is 30, so 12 to 2 is 60). If you were to draw a line from the tip of the hour hand, through the center of the clock, and out to the opposite side, the angle between the minute hand and that imaginary line would be 120 degrees! They'd be supplementary.
So, the next time you see a straight line, or something that looks like it could be a straight line broken into two parts, you've got a little superpower. You can instantly figure out what those parts add up to. It's like having a built-in protractor for straight lines!
The beauty of math, and especially geometry, is that it's often about recognizing patterns and relationships. Supplementary angles are just one of those fundamental relationships. They're like the quiet, dependable friends in the angle family. They always add up to a specific amount, always creating that sense of completeness with a straight line.
So, to wrap it up in a friendly bow: if you've got two angles chilling together and they form a perfect straight line when you smoosh them side-by-side, they're supplementary. And if one of them is a cozy 60 degrees, its partner has to be a generous 120 degrees to make that 180-degree party happen. It's a simple, elegant truth of the geometric universe. Keep your eyes peeled; you might be surprised where you spot these supplementary pairs out in the wild!
