Triangle Congruence Sss Sas Asa Aas Hl Worksheet Answer Key

So, picture this: I’m in my early teens, a time of, let’s just say, explosive growth in awkwardness and questionable fashion choices. We were doing geometry, which, honestly, felt like deciphering ancient hieroglyphs most days. My math teacher, bless her patient soul, was trying to explain… triangle congruence. And I’m sitting there, staring at these perfectly identical triangles on the board, thinking, "Okay, so they look the same. Does that mean they are the same?" It was a genuine existential crisis for my 13-year-old brain.
I mean, sometimes things look the same, right? Like my two favorite band t-shirts. They’re both black, both have the same logo. But one’s got a tiny coffee stain from that one epic concert, and the other’s a little more faded from endless laundry cycles. Are they truly identical? The answer, I learned eventually, is no. And this, my friends, is where the magic – or at least the math – of triangle congruence comes in.
It turns out, in the rigid, beautiful world of geometry, "looking the same" isn't quite good enough. We need proof. And for triangles, that proof comes in a few surprisingly elegant forms. Think of it like a secret handshake, a specific sequence of moves that guarantees two triangles are not just twins, but identical clones. And today, we’re going to peek behind the curtain, get a little cozy with these proofs, and maybe, just maybe, demystify that infamous “worksheet answer key.” You know the one. The one that’s probably staring at you from your desk right now, whispering sweet nothings of confusion.
The Not-So-Secret Life of Identical Triangles
Why should we even care about whether two triangles are congruent? Well, besides passing geometry class (a noble pursuit, I assure you), understanding congruence is foundational for so much more. It’s like learning your ABCs before you can write poetry. When you can prove two triangles are identical, you automatically know that all their corresponding parts are identical too. Their angles will be the same, their sides will be the same length. Boom! Suddenly, you can solve for unknown angles and lengths. It’s like having a cheat code for the geometry universe.
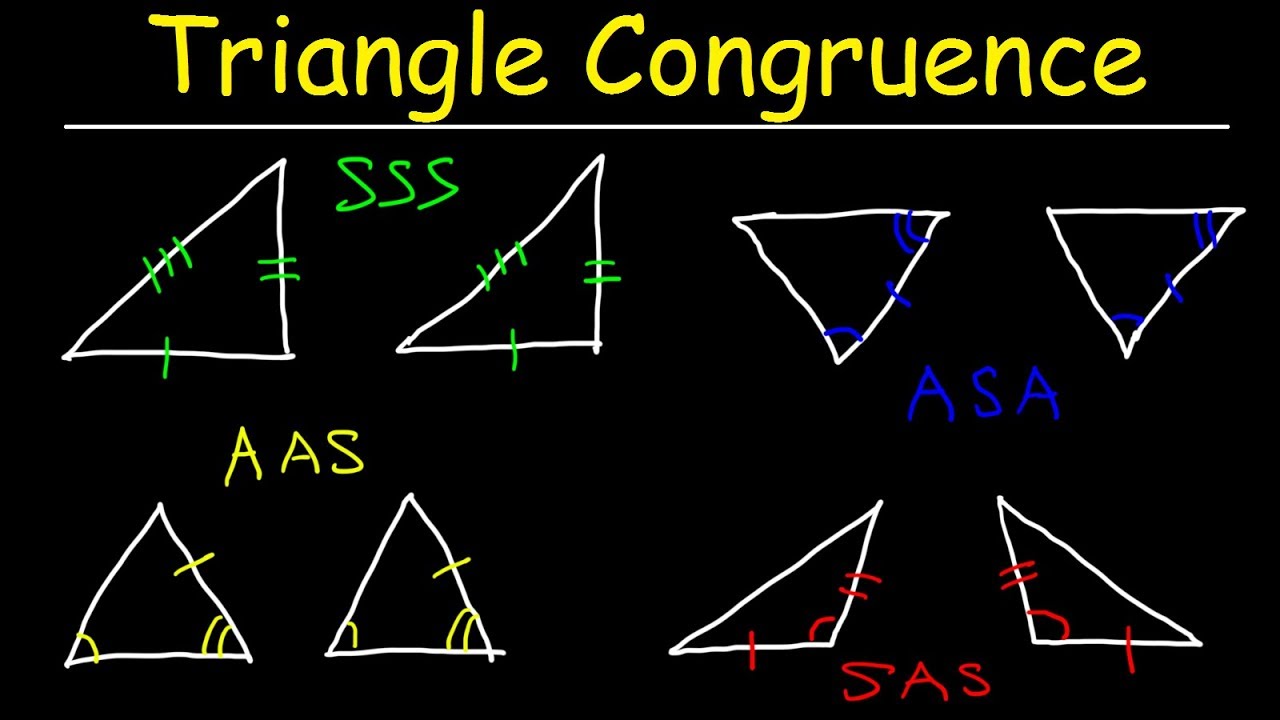
So, let’s ditch the abstract and get down to business. We’ve got our main players: SSS, SAS, ASA, AAS, and HL. These aren’t random letters thrown into a math blender, oh no. These are the keys that unlock the congruence puzzle. They are the specific conditions that, if met, tell us, with absolute certainty, that two triangles are indeed congruent. No more guesswork, just pure mathematical logic. Isn’t that kind of cool?
SSS: The Side-Side-Side Story
This is probably the most intuitive one. Imagine you’ve got three rulers, each of a specific length. You lay them out on a table, connect the ends, and what do you get? A triangle! Now, if I give you another set of three rulers with the exact same lengths and you do the same thing, you’re going to end up with a triangle that is exactly the same size and shape as the first one. No matter how you rotate it, it’s going to fit perfectly. That’s SSS, or Side-Side-Side.
If all three sides of one triangle are congruent to the corresponding three sides of another triangle, then the triangles are congruent. It’s that simple. Think about building something. If you have the exact same set of wooden planks (sides), you can build the exact same structure (triangle). There's no room for variation. It’s like a recipe where the ingredients (side lengths) dictate the final product. Pretty neat, huh? This is the bedrock, the most straightforward way to declare congruence.
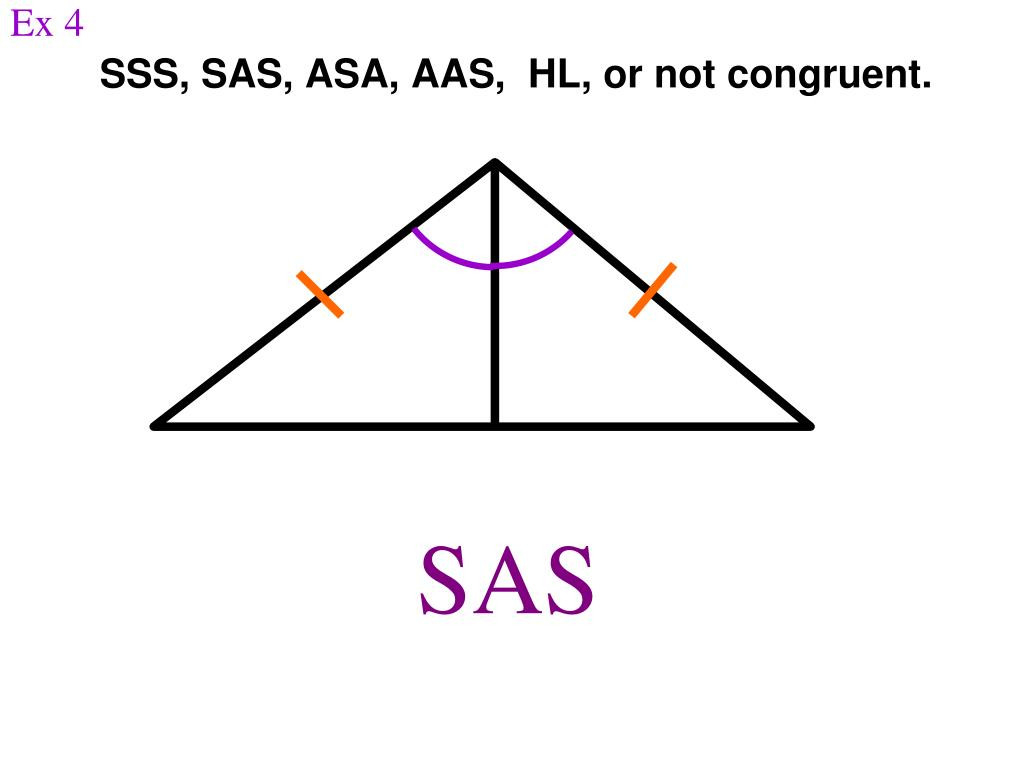
SAS: The Angle in Between is Key
Now, things get a tiny bit more specific. SAS stands for Side-Angle-Side. Here’s the trick: it’s not just any side, any angle, any side. The angle has to be between the two sides. So, you need two sides of one triangle to be congruent to two corresponding sides of another triangle, AND the angle formed by those two sides (the included angle) must also be congruent.
Why is the "in between" part so important? Imagine you have two sticks of equal length, and you connect them at one end. You can then swing them open to create different angles. The size and shape of the triangle you form depends entirely on that angle. If you keep the angle the same and use sticks of the same length, you’ll always get the same triangle. But if you change just one of the side lengths, even slightly, or the angle, you’re going to get a different triangle. So, that included angle is the crucial piece of information. It locks everything into place, just like that perfect angle on a well-constructed shelf. Don't you just love when things fit perfectly?
ASA: The Angle-Side-Angle Dance
Moving right along, we have ASA, which stands for Angle-Side-Angle. This one is a little like SAS, but the order is different. Here, you need two angles of one triangle to be congruent to two corresponding angles of another triangle, AND the side between those two angles must also be congruent.
Think about it this way: if you know two angles and the side connecting them, you’ve essentially defined the entire triangle. Why? Because the third angle is automatically determined by the fact that the sum of angles in a triangle is always 180 degrees. So, if you have two angles and the side connecting them, you know the shape. And if another triangle has the same two angles and the same connecting side, it has to be identical. It’s like tracing a path. If you know two turns you make and the distance you walk between them, you know exactly where you’ll end up. This is why ASA works. It’s a precise way to map out a triangle.
AAS: The Angle-Angle-Side Surprise
Here’s where things get a little interesting, and maybe a touch ironic. We have AAS, or Angle-Angle-Side. Now, notice the side is not between the two angles. It’s one of the other sides. So, you have two angles of one triangle congruent to two corresponding angles of another triangle, and a non-included side congruent to the corresponding non-included side.
You might be thinking, "Wait a minute! If the side isn't between the angles, how can it guarantee congruence?" Ah, but remember our little secret from ASA? The third angle is always determined! So, if you know two angles, you automatically know the third angle. That means AAS is actually equivalent to ASA. If you know two angles and a side, you implicitly know the third angle, which makes it an ASA situation in disguise! It’s like finding a hidden bonus level in a video game – you thought you knew the rules, but there’s an extra way to win. Isn't that delightful?

HL: The Right-Triangle Special Case
Finally, we have a special rule just for right triangles: HL, which stands for Hypotenuse-Leg. This is a big deal because it only applies to right triangles. If you have two right triangles, and their hypotenuses are congruent, AND one pair of corresponding legs is congruent, then the triangles are congruent.
Why is this special? Because in a right triangle, we have that handy Pythagorean theorem ($a^2 + b^2 = c^2$). If we know the hypotenuse (c) and one leg (say, a), we can always find the other leg (b). So, if two right triangles have the same hypotenuse and the same leg, their other legs must also be the same length. Therefore, by SSS, they are congruent. HL is just a shortcut, a more efficient way to get to the same conclusion specifically for our right-angled friends. It’s like having a special express lane for right triangles. Who doesn't love an express lane?
The Infamous Worksheet Answer Key
Okay, so now we have our tools: SSS, SAS, ASA, AAS, and HL. When you’re faced with a worksheet full of triangles, the task is usually to determine which of these postulates or theorems can be used to prove the triangles are congruent, or if they can be proven congruent at all. You’re looking for matching sides and angles, being super careful about whether an angle is included or not, and always remembering the special case for right triangles.
The answer key? It’s your confirmation. It’s the librarian telling you you’ve indeed found the correct book. When you’ve gone through the steps, identified the congruent parts, and applied one of our congruence rules, you check the answer key to see if you’re on the right track. If it says "SAS," and you identified two congruent sides and the included congruent angle, you’re golden! If it says "Not Congruent," and you couldn't find a match using any of the rules, then that’s also a valid conclusion. It’s not a failing if they aren’t congruent; it just means they don’t meet the strict geometric definition of being identical.

Sometimes, the answer key might have an explanation that makes your brain do a little somersault. Maybe it uses a different postulate than you did, but it's still correct. For example, if you used AAS and the key says ASA, don't panic! As we saw, they can be equivalent. The key is understanding why the answer is what it is. Don't just blindly accept it. Wrestle with it! See if you can prove the proof yourself. That’s where the real learning happens, far beyond just matching letters to answers.
And let’s be honest, sometimes the answer key feels like it’s written in a secret code. You look at it, you look at your work, and you think, "How on earth did they get that?" Take a deep breath. Go back to the definition of each postulate. Did you correctly identify the corresponding parts? Was the angle truly included? Did you accidentally use SSA (Side-Side-Angle) which, by the way, is not a congruence postulate – it’s the infamous “ambiguous case” where you might have zero, one, or two possible triangles? Oof, that one’s a doozy! Always be on the lookout for it.
So, when you’re staring down that worksheet, remember: you’re not just filling in bubbles or writing down letters. You’re becoming a geometric detective. You’re looking for evidence, applying logical rules, and making definitive conclusions. The SSS, SAS, ASA, AAS, and HL are your magnifying glass, your fingerprint kit, your lie detector. And the answer key? It's the final verdict, the confirmation that your detective work was sound.
Keep practicing, keep questioning, and don’t be afraid to go back to the basics. Those triangles might look simple, but the rules that govern their congruence are pretty powerful. And who knows, maybe one day you’ll be building bridges or designing airplanes, and all this talk of SSS and SAS will suddenly make perfect, practical sense. Until then, happy congruent-ing!
