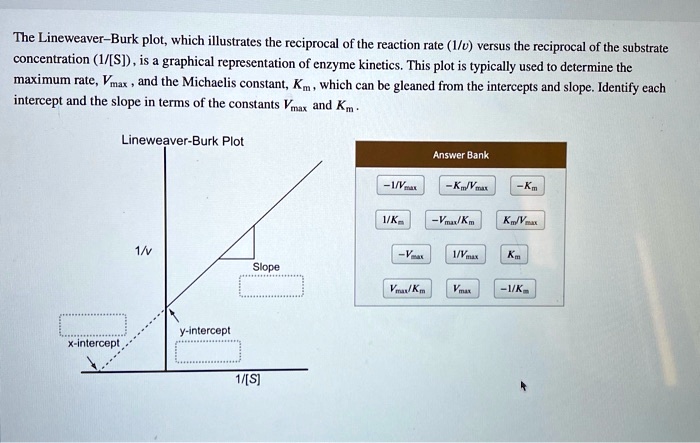
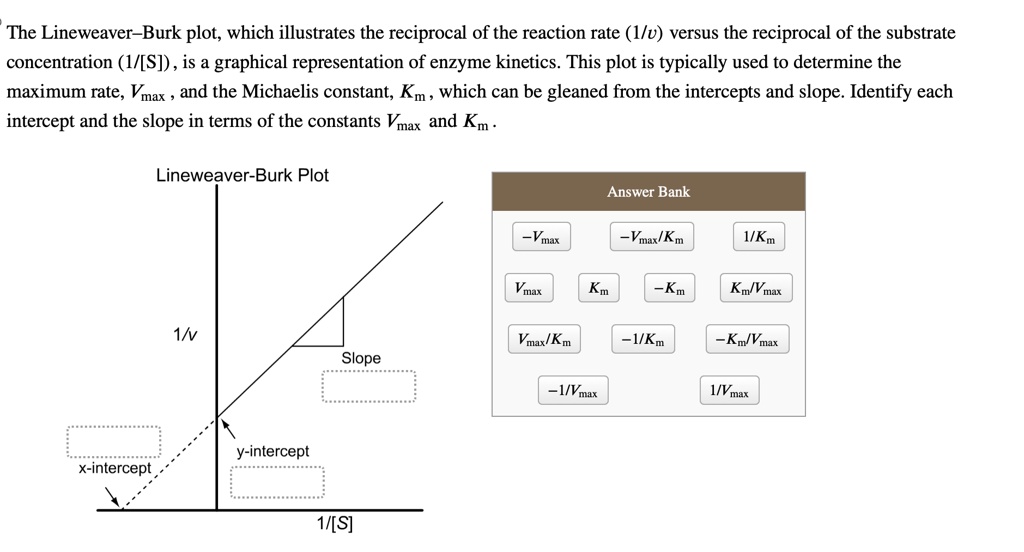
The Lineweaver Burk Plot Which Illustrates The Reciprocal
Ever felt like you were chasing your tail when trying to understand something super complicated in science? Well, buckle up, buttercup, because we're about to dive into a little piece of graphing magic that makes the reciprocal behave like a happy puppy instead of a grumpy badger. It’s called the Lineweaver-Burk Plot, and it’s basically a superhero costume for awkward data.
Imagine you're trying to figure out how fast your favorite ice cream truck drives. You could measure its speed at different distances, but sometimes the numbers get all jumbled. It’s like trying to count jellybeans in a jar – a little messy!
The Lineweaver-Burk Plot swoops in like a caped crusader and says, "Hold on a minute! Let's flip those numbers upside down!" It sounds crazy, right? Like turning your whole world upside down just to find your keys.
But here’s the secret sauce: when you take the reciprocal of your data – meaning you do one divided by that number – something amazing happens. Suddenly, a bunch of wiggly, unpredictable lines straighten out into beautiful, elegant lines. It's like a messy room suddenly becoming perfectly organized with a wave of a wand!
Think about trying to understand how a ridiculously popular restaurant gets all its customers. You could track how many people show up over time, and it might look like a chaotic stampede. It’s like trying to hear a single conversation in a rock concert.
But what if we looked at the inverse of that? What if we looked at how long it takes for the restaurant to serve a certain number of people? Suddenly, the mayhem starts to make sense. The Lineweaver-Burk Plot is the tool that helps us see this flipped-over perspective.
It’s particularly awesome in the world of biology, especially when scientists are studying how enzymes (those amazing little biological machines) do their job. They’re trying to figure out how quickly these enzymes can munch through their favorite molecules. It's like timing a cheetah on a treadmill, but much cooler.

Sometimes, the raw data about enzyme speed can be a bit… well, persnickety. It doesn't always want to play nice and form a neat pattern. It’s like trying to build a perfect sandcastle on a windy beach – frustrating!
Enter the Lineweaver-Burk Plot! Scientists take the reciprocal of the reaction rate (how fast the enzyme is working) and the reciprocal of the substrate concentration (the amount of "food" the enzyme has). And poof!
Instead of a confusing scatter of dots, they get a straight line. A glorious, predictable, straight line. It’s like finding a hidden shortcut on a long, winding road.
This straight line isn't just pretty to look at; it’s packed with information. The point where the line crosses the y-axis (that’s the vertical one, for the graphing novices) tells you something super important about the enzyme. It’s like the enzyme’s secret handshake!
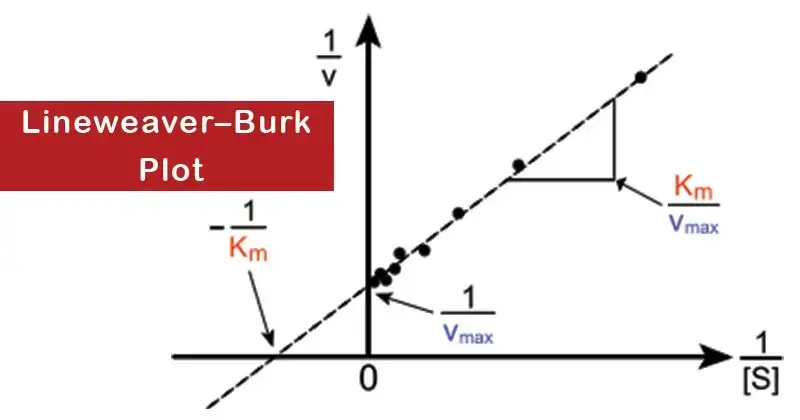
And the slope of the line? That's another juicy bit of data, giving you even more clues about how that enzyme is behaving. It’s like the enzyme’s personal biography.
So, why the reciprocal? Why flip everything upside down? It’s all about making things easier to see and understand. Imagine you’re trying to measure how much coffee is left in a mug by looking at how much you've drunk. It’s much easier to track the remaining coffee, right? The reciprocal is like that – it helps us focus on the essential piece of the puzzle.
Think about baking a cake. You follow a recipe, and it tells you how much of each ingredient to use. If you want to make half a cake, you just halve the ingredients. Easy peasy.
But what if the recipe was a bit more abstract, like how many eggs you need for a certain number of happy smiles generated by a batch of cookies? That’s where things get tricky. You'd want to understand the relationship between cookies and smiles, but the raw numbers might be confusing.
The Lineweaver-Burk Plot, with its love for the reciprocal, helps untangle these sorts of relationships. It takes data that might look like a bird's nest after a hurricane and turns it into a perfectly organized bookshelf. It’s that satisfying.
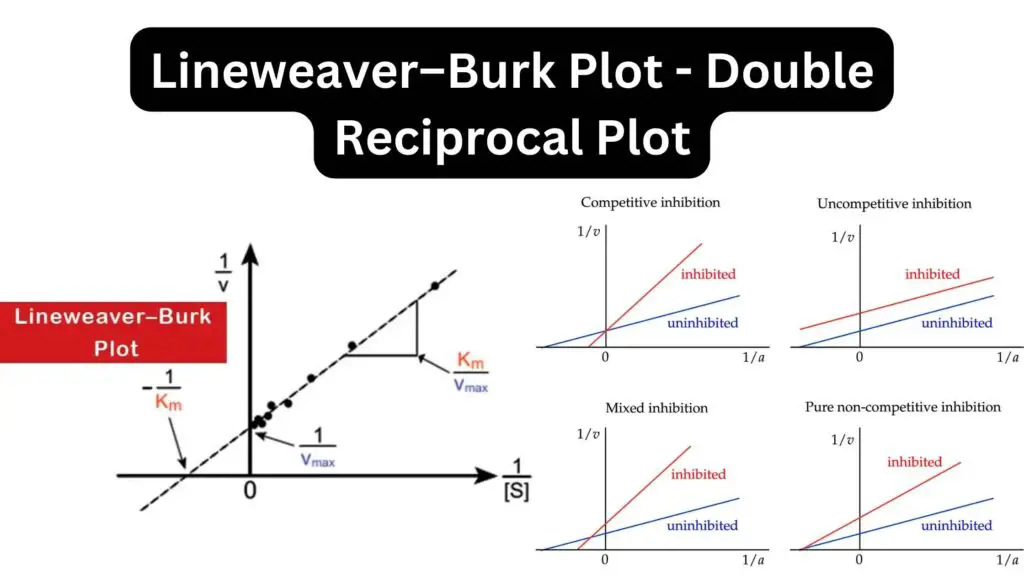
It's especially useful for comparing different situations. For example, if you're testing different versions of an enzyme, you can plot them all on the same Lineweaver-Burk Plot. Then, you can easily see which one is the superstar and which one needs a little more training. It's like having a scoreboard for your experiments!
Let’s talk about speed limits. Imagine you’re trying to understand how traffic flow changes as the speed limit goes up. The raw data might be all over the place, with slow days and fast days. It’s like trying to predict the weather by looking at a single cloud.
But if you look at the inverse of the traffic flow – maybe how long it takes for a certain number of cars to pass a point – and then plot that using the Lineweaver-Burk approach, you might see a much clearer picture. The lines will straighten out, showing you the underlying trend more clearly. It's like getting x-ray vision for traffic.
So, while the word "reciprocal" might sound a bit intimidating, it's really just a fancy way of saying "flipped upside down." And when you combine that with the cleverness of the Lineweaver-Burk Plot, you get a powerful tool that simplifies complex scientific data. It’s the scientific equivalent of finding a cheat code!
This plot is a favorite for a reason. It takes the messy, chaotic reality of experimental results and presents it in a clean, interpretable format. It’s the unsung hero of many a scientific paper, making those intricate biological processes seem almost… dare I say… obvious.
Think of it like this: you have a bunch of puzzle pieces scattered all over the floor. It's a mess! You can't see the whole picture. But the Lineweaver-Burk Plot is like the puzzle box lid. It shows you the clear image, and by using the reciprocal trick, it helps you connect those scattered pieces into that beautiful, ordered picture.
It’s not about making things harder, it’s about making them clearer. It’s about taking a complex system and finding the elegant simplicity hidden within. The Lineweaver-Burk Plot is a testament to that. It’s a little bit of graphing genius that makes understanding the reciprocal feel like a walk in the park. And who doesn't love a good walk in the park, especially when it leads to scientific enlightenment?
So, next time you hear about the Lineweaver-Burk Plot, don’t run for the hills! Just imagine flipping things upside down, and a world of clear, straight-line science will open up before you. It’s a wonderfully simple yet powerful idea, and it truly makes the reciprocal sing!
