The Expression 36a+16b Factored Using The Gcf Is
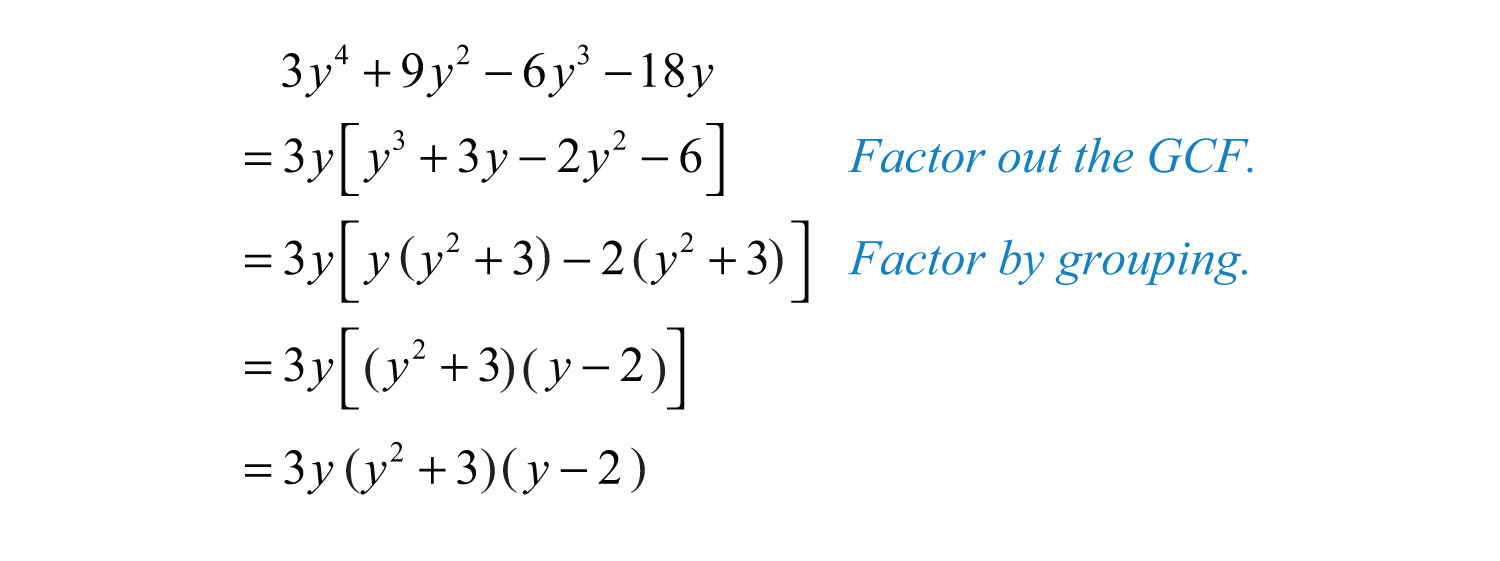
Imagine you’re at a big, boisterous family reunion. Everyone’s got their own unique personality, their own quirks and strengths. You’ve got Aunt Carol, who always brings her famous apple pie, and Uncle Bob, who can tell a joke about anything. And then there’s little Timmy, who’s just a bundle of energy, running around with his cousins.
Well, sometimes, expressions in math can feel a bit like that big family. They’re made up of different parts, all jumbled together. We’ve got our 36a, strutting in like the popular kid, and our 16b, maybe a little quieter but with its own special charm. They’re a pair, for sure, but they’re also their own distinct entities.
Now, what if we told you there's a way to find a sort of "family resemblance" between these two? A way to find something they both share, something that unites them under one happy umbrella. It’s like finding out Aunt Carol and Uncle Bob secretly love the same cheesy 80s music. Surprising, right?
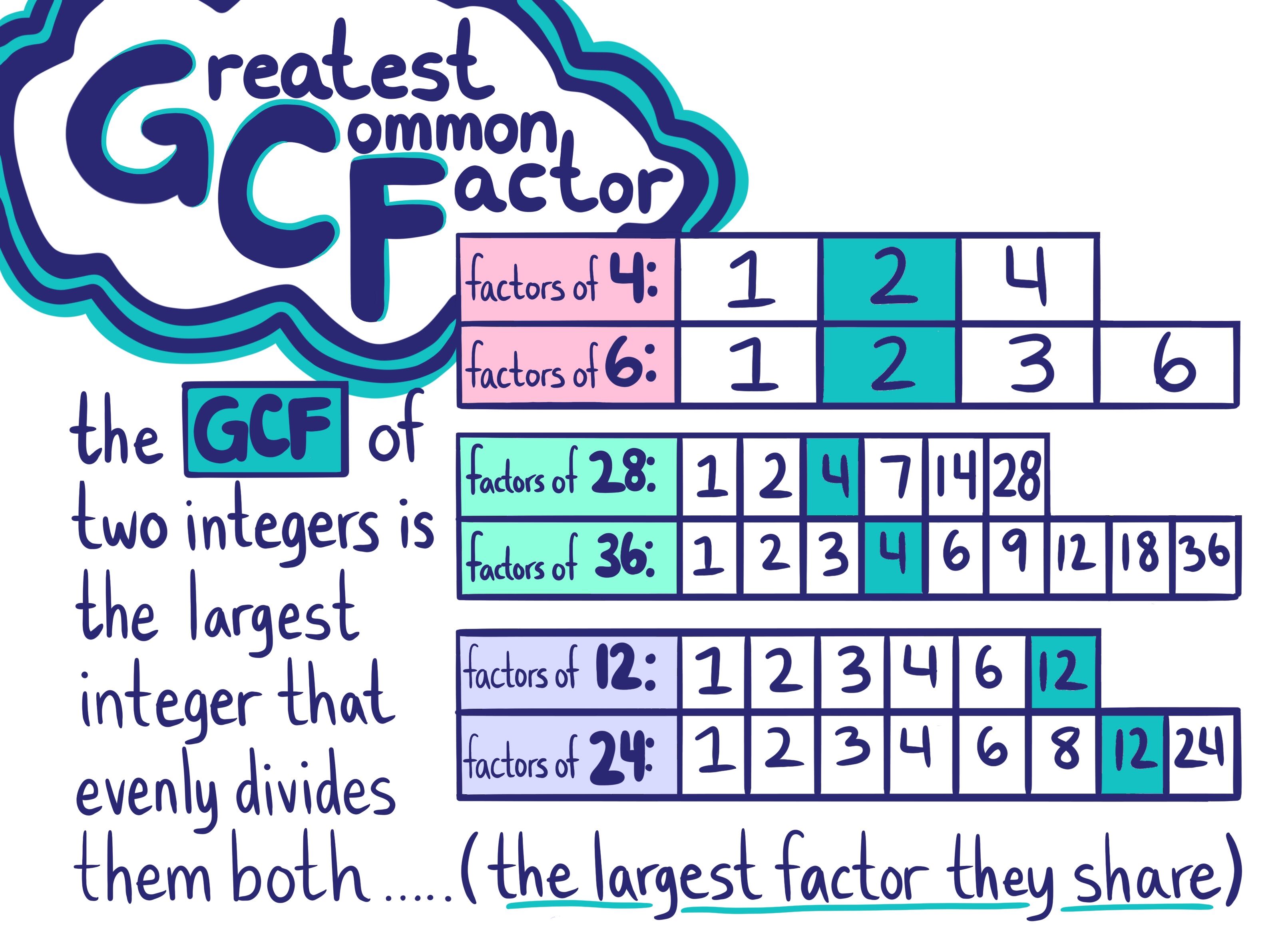
This special family resemblance we're talking about is called the Greatest Common Factor. Think of it as the ultimate shared trait, the biggest thing these two parts have in common. It’s not just a little something; it's the most significant thing they can both be divided by evenly.
So, we’re looking at 36a and 16b. We want to find the biggest number that can divide into both 36 and 16 without leaving any awkward remainders. It’s like trying to find the biggest perfectly cut slice of pizza that can be made from two different-sized pies. You want the biggest possible equal sharing!
Let’s think about the numbers. For 36, we have numbers like 1, 2, 3, 4, 6, 9, 12, 18, and 36. For 16, we have 1, 2, 4, 8, and 16. See how some numbers pop up on both lists? Those are the common factors, the shared traits of our mathematical family.
We’re looking for the greatest one. The biggest number that appears on both lists. Drumroll, please… it’s a 4! Isn’t that neat? This little number 4 is the secret handshake, the inside joke, the unifying force between 36a and 16b.

But wait, there's more! It's not just about the numbers. We also need to look at the letters. Do 36a and 16b share any letters in common? In this case, one has an 'a' and the other has a 'b'. They're like siblings who chose different majors in college; they don't have the exact same course of study.
So, the GCF for our entire expression, the 36a + 16b, is just the number 4. It’s the single, shining star that both parts of our expression can proudly claim as their own. It’s the common ground where they can meet and be understood.
Now, what do we do with this amazing discovery? We use it to make our expression tidier, more organized, and frankly, a little more elegant. It’s like folding your laundry perfectly instead of just shoving it in a drawer. Everything looks and feels better!
We take that GCF, that wonderful number 4, and we pull it out. It’s like the host of the party, standing at the entrance, greeting everyone. We put it outside the parentheses, saying, "Hey everyone, come on in, but remember our common bond!"
Then, inside the parentheses, we put what’s left after we’ve “divided” each part of the original expression by our GCF. Think of it as assigning each family member a seat at the reunion table after the big greeting. They’re still together, but now they’re in their designated spots.
![[ANSWERED] What is the GCF of the expression below that could be use to](https://media.kunduz.com/media/sug-question-candidate/20240108162736487938-6481057.jpg?h=512)
So, if we take 36a and divide it by 4, what do we get? We get 9a. That’s the first guest arriving at the table. Then, we take 16b and divide it by 4. We get 4b. That’s the next guest!
And the operation that was between them? That addition sign? It stays right there, holding them together inside their new, cozy space. It’s like the place cards at the table, keeping the order and the family feeling.
So, the expression 36a + 16b, when we factor out its GCF, becomes 4(9a + 4b). Isn't that a beautiful transformation? It’s like seeing a messy room suddenly become neat and orderly, or hearing a jumbled sentence become clear and concise.
It’s a way of saying, "Look, these two things are related! They have this common factor, this shared essence, and by pulling it out, we can see their structure more clearly." It's like noticing that your two best friends, despite their differences, both have a fantastic sense of humor. That's a wonderful thing to discover!
This process, this factoring using the GCF, is like finding a hidden treasure. It reveals a simpler, more fundamental truth about the expression. It's like realizing that the complex recipe you've been struggling with actually has just a few core ingredients that make it all work.
And the best part? It’s not just about making math look pretty. This technique is super useful in solving bigger problems, in simplifying complicated equations, and in seeing patterns that were previously hidden. It’s the secret weapon that mathematicians use to conquer complex challenges.
Think of it as learning a magic trick. Once you know the secret of the GCF, a whole new world of mathematical possibilities opens up to you. You can rearrange things, simplify them, and make them easier to understand. It’s empowering!
So, the next time you see an expression like 36a + 16b, don't just see a jumble of numbers and letters. See a mathematical family, a little unit with its own relationships and common bonds. And remember the magic of the GCF, the amazing tool that helps us uncover these hidden connections.
It’s a reminder that even in the seemingly abstract world of numbers, there's order, there's structure, and there's a beautiful simplicity waiting to be discovered. It’s like finding a perfectly matched pair of socks in your laundry – a small victory, but one that brings a little bit of joy and order to your day.
So, to recap, the expression 36a + 16b, when factored using its Greatest Common Factor, elegantly transforms into 4(9a + 4b). It’s a testament to the power of finding common ground, a little mathematical hug that makes everything more manageable and, dare we say, a bit more fun!

It’s about seeing the forest for the trees, or rather, seeing the united family for the individual members. This simple act of factoring reveals a deeper truth, a more organized reality. And that, in itself, is a wonderful thing to appreciate.
So, go forth and find those GCFs! Uncover those hidden connections. Make math a little less daunting and a lot more delightful. Because at its heart, math is just another language, and understanding its grammar, like the GCF, unlocks a whole new world of understanding and fun!
Consider this your official invitation to the wonderful world of factoring. It’s a place where numbers and letters come together, where common ground is celebrated, and where even the most complex expressions can be simplified with a little bit of cleverness. And that, my friends, is something to be cheered about!
So, when you encounter 36a + 16b, remember the little number 4. That's your key, your golden ticket to simplification. It's the unsung hero, the quiet connector, making all the difference. And that’s a pretty heartwarming thought, don’t you think?
It’s like finding out that your favorite quirky character in a book has a surprising connection to another character you love. It adds a whole new layer of appreciation and makes the story even richer. And that’s exactly what factoring with the GCF does for our expressions!
