The Electric Potential Inside A Parallel-plate Capacitor __________.
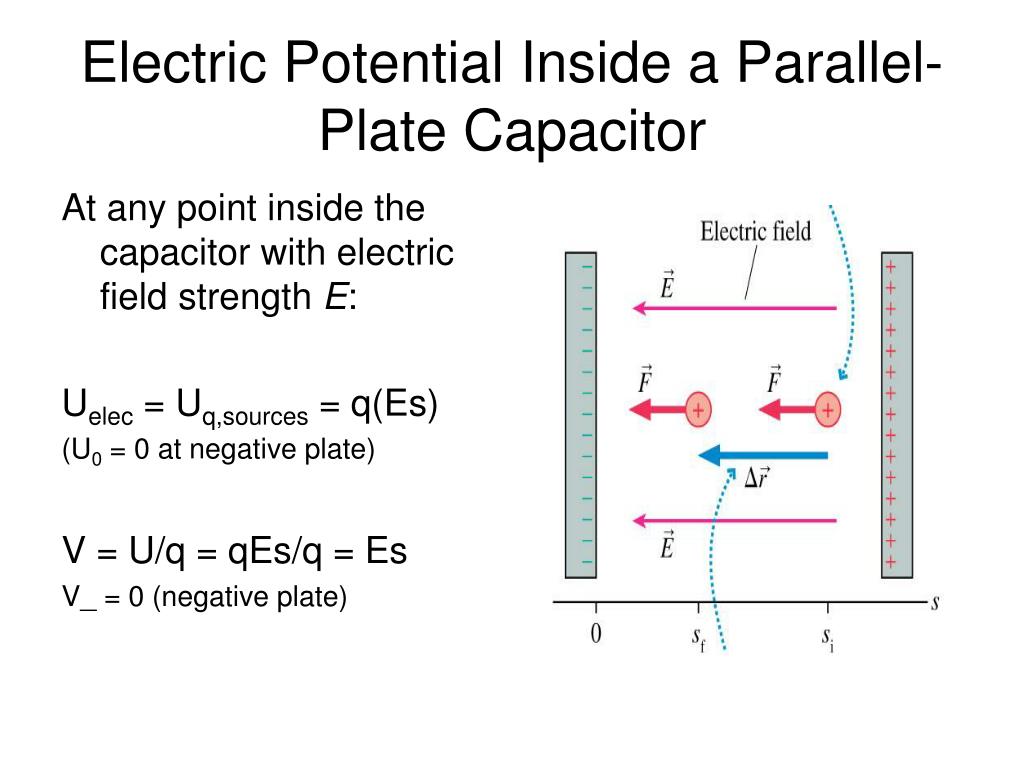
So, you wanna talk about what’s going on inside a parallel-plate capacitor? Buckle up, buttercup, because we’re diving into the wild, wonderful world of electric potential. Imagine this: you’ve got two shiny, flat metal plates, chilling right next to each other. Like roommates who are so close, but technically, they're not touching. Thank goodness, or we’d have a short circuit, and nobody wants that kind of drama.
Now, these aren't just any old plates. These are the Beyoncé and Jay-Z of the capacitor world – they've got a whole lot of charge hanging out on them. One plate, let’s call her Patty Positive, is positively buzzing with positive charges. The other, Nancy Negative, is practically swimming in a sea of negative charges. It’s like a party where everyone brought their opposite-gendered twin and they're all incredibly attracted to each other, but again, no touching allowed.
What happens when you have all this charge jiggling around? It creates something called an electric field. Think of it as an invisible force field, like in Star Trek, but instead of phasers, it’s got little arrows pointing from Patty Positive to Nancy Negative. These arrows represent the direction of the push or pull that a tiny test charge would feel if you dared to drop one in there. Pretty neat, huh?
But here’s where it gets really interesting, and frankly, a little mind-bending: electric potential. If the electric field is the force, the potential is the energy associated with that force. It’s like the difference between being able to push a boulder versus having the energy to actually push that boulder all the way up a hill. You don’t want to be at the bottom of that hill, trust me.
Inside our perfectly behaved parallel-plate capacitor, something truly special happens with this electric potential. Unlike that grumpy old Coulomb’s Law, which makes potential drop off with distance like a teenager’s interest in homework, the potential inside the capacitor is remarkably… constant. Whoa. Mind. Blown.

Yes, you heard me! Between those two plates, as long as you’re not peeking too close to the edges (we’ll get to that scandalous behavior later), the electric potential is the same, everywhere you look. It's like a perfectly flat, perfectly manicured golf course of electrical energy. No bumps, no divots, just smooth sailing.
The "Noooo, It's Not Fair!" Factor
This might seem a bit unfair, right? Patty Positive is all juiced up, and Nancy Negative is practically vibrating with excitement, and yet, the potential is uniform? It’s like they’re both at the same altitude on a perfectly flat plain. This is because of the magic of those infinite, or at least really, really large, parallel plates. The electric field lines are perfectly parallel and evenly spaced, pointing straight from one plate to the other. No funny business.
Think of it like this: imagine you’re hiking up a really steep hill. The higher you go, the more potential energy you have. But what if the hill was suddenly replaced by a giant, perfectly level plateau? The moment you step onto that plateau, your altitude, and therefore your potential energy relative to the ground, stops changing. That's kind of what's happening inside the capacitor, but instead of altitude, it's electric potential.
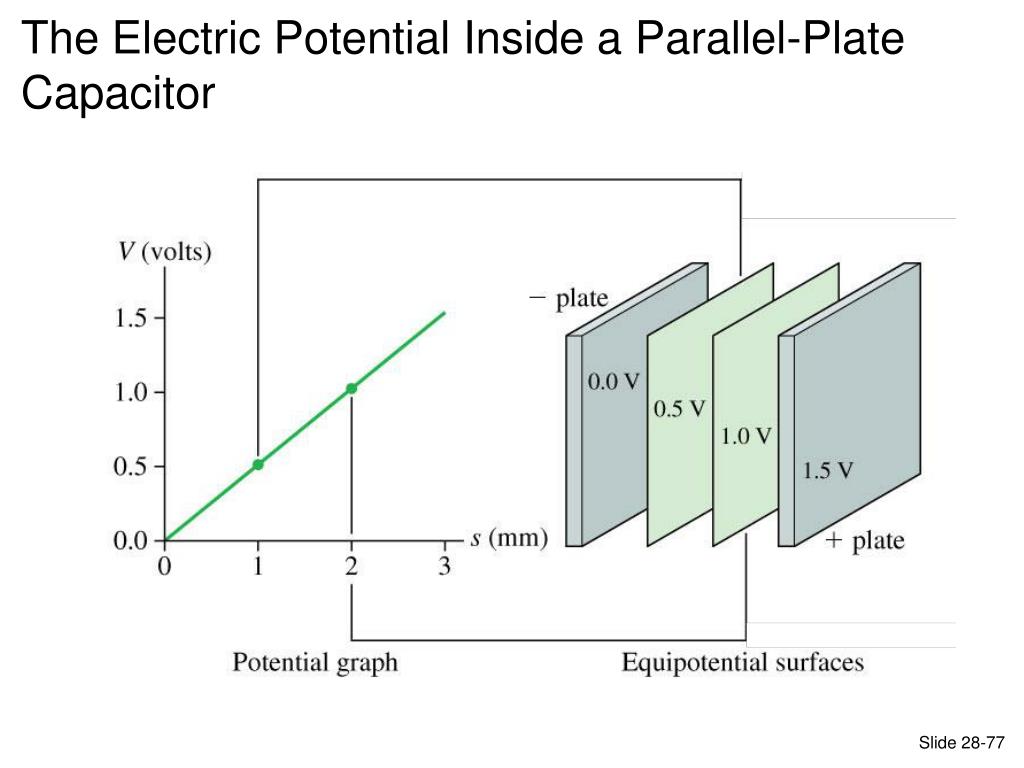
So, if you were a tiny little electron, say, Eddie Electron, and you were zipping around between the plates, you wouldn't feel any particular urge to go left or right based on potential. The "uphill" or "downhill" is the same everywhere. It’s a bit like being in a perfectly balanced elevator – you don’t feel like you’re moving up or down any faster within the cabin itself, even though the elevator is on its way to a different floor.
This is a crucial difference from, say, the potential around a single point charge. That’s like a volcano – the potential is highest right at the crater (the charge) and drops off dramatically as you move away. But our capacitor? It’s more like a giant, flat-topped mountain. High potential, yes, but spread out evenly.

The "Edge Case" Scandal
Now, like any good story, there are always a few characters who don't play by the rules. These are the folks hanging out near the edges of the capacitor plates. Oh, the drama! At the edges, those nice, straight, parallel electric field lines start to get a little… wiggly. They say, "You know what? I think I'll take a detour!" They start to bend outwards, like a crowd of people at a concert trying to get a better view of the stage.
This "fringing field," as the fancy physics folks call it, means the electric field is no longer perfectly uniform at the edges. And guess what? If the field isn't uniform, then the potential isn't uniform either! It’s like the plateau suddenly has a slight slope at the rim. So, while the bulk of the capacitor is a haven of constant potential, the edges are a bit more… exciting. Just a little bit.
This is why, in idealized physics problems, we often assume the plates are infinitely large. It’s a convenient fiction that lets us ignore the edge-case drama and focus on the beautiful simplicity of the uniform potential. In the real world, though, capacitors have edges, and those edges can sometimes matter, especially if you're trying to cram a ton of charge into a small space.

Why Should You Care? (Besides the Free Coffee)
So, why is this whole uniform electric potential thing such a big deal? Well, it’s fundamental to how capacitors work. The fact that the potential is constant means that the work you have to do to move a charge from one plate to the other is consistent, regardless of the path you take between the plates. This consistency is what allows capacitors to store energy so efficiently.
It also leads to a very simple relationship between the electric field (E), the potential difference (V), and the distance between the plates (d). For that perfectly uniform field inside the capacitor, you get the super-simple equation: V = E * d. That’s it! No complicated integrals, no weird functions. Just straight multiplication. It’s the physics equivalent of finding a $20 bill in an old coat pocket – pure, unadulterated joy.
The electric potential inside a parallel-plate capacitor is a testament to the elegance of physics. It’s a zone of calm, predictable energy, a perfect plateau in a sometimes chaotic electrical landscape. So next time you see a capacitor, give it a nod. It’s not just a bunch of metal plates; it’s a little pocket of electrical tranquility, with just a hint of edge-of-your-seat excitement.
