Surface Area Of Triangular Prism Worksheet With Answers Pdf

Hey there, fellow math adventurer! So, you’ve stumbled upon the magical world of triangular prisms, huh? Don’t worry, it’s not as pointy as it sounds (well, maybe a little, but in a good, geometric way!). Today, we’re going to chat all about the surface area of triangular prisms. And guess what? We’ve got your back with a super handy worksheet complete with answers! Yep, you heard that right. No more scratching your head and wondering if you’ve accidentally invented a new type of pizza slice. We’re talking about making this whole surface area thing a total breeze.
Think of a triangular prism like a Toblerone box, or maybe a really fancy slice of cake. It’s got two triangular ends and three rectangular sides connecting them. So, when we talk about its "surface area," we're basically figuring out the total area of all those flat surfaces. It’s like you’re wrapping a present, and you want to know exactly how much wrapping paper you’ll need. No more awkward gaps or way too much overlap – just the perfect amount!
Now, calculating this might sound a bit intimidating at first. But trust me, it’s really just a few simple steps. We’re going to break it down so it’s as easy as, well, eating a triangular piece of chocolate. And for those moments when you’re not quite sure if your answer is on the right track, that’s where our awesome surface area of triangular prism worksheet with answers PDF comes in. It’s your secret weapon, your trusty sidekick, your mathematical genie in a bottle!
Let’s dive into the nitty-gritty of how we actually find this surface area. It’s not rocket science, and it’s definitely not advanced calculus (thank goodness!). We’re going to stick to good ol’ geometry, the kind that makes sense and doesn’t give you a headache. So, grab a metaphorical (or literal!) snack, get comfy, and let’s get this geometric party started!
Unpacking the Triangular Prism: What's What?
Before we start measuring and calculating, let’s make sure we’re all on the same page about what a triangular prism is. Imagine you take a triangle, and then you extrude it, like pulling it out into a longer shape. That’s pretty much it! It has:
- Two congruent triangular bases: These are the pointy ends. They’re identical triangles.
- Three rectangular faces: These are the sides that connect the two triangles. They’re always rectangles.
So, to find the total surface area, we need to find the area of those two triangles and the area of each of those three rectangles, and then add them all up. Simple, right? Well, almost. We need to know a few key measurements.
The Essential Measurements You’ll Need
For our triangular prism adventure, we’ll be looking for:
- The base of the triangle (b): This is one of the sides of the triangular base.
- The height of the triangle (h): This is the perpendicular distance from the base to the opposite vertex (the pointy bit) of the triangle. Remember, perpendicular is the keyword here – it forms a perfect 90-degree angle!
- The lengths of the other two sides of the triangle (let’s call them s1 and s2): Sometimes you might have an equilateral triangle (all sides equal) or an isosceles triangle (two sides equal), or a scalene triangle (all sides different). We need to know these lengths.
- The height of the prism (H): This is the distance between the two triangular bases. Think of it as how "long" the prism is.
Got all that? Great! Now we can start calculating!
The Formula Fiesta: Cracking the Surface Area Code
Alright, let’s get down to business with the actual formula. It looks a bit more imposing than it actually is, so don't let it scare you. We’re going to break it down into easy-to-digest pieces.
Area of the Triangular Bases
First things first, we need the area of those two triangular ends. The formula for the area of a triangle is:
Area of one triangle = 1/2 * base * height
Since we have two identical triangles, the total area of both bases is:
Area of two triangles = 2 * (1/2 * b * h) = b * h
See? That wasn't so bad! It simplifies nicely. So, grab those triangle measurements and plug them in. Easy peasy lemon squeezy!
Area of the Rectangular Faces
Now for the sides! Remember, a prism has three rectangular faces. The area of any rectangle is:
Area of a rectangle = length * width
In our prism case, the "width" of each rectangle is the height of the prism (H). The "length" of each rectangle is one of the sides of the triangular base. So, the areas of our three rectangular faces will be:

- Rectangle 1 Area = s1 * H
- Rectangle 2 Area = s2 * H
- Rectangle 3 Area = b * H (using the base we defined earlier)
If the triangular base is equilateral, then all its sides are equal, and you’ll have three identical rectangles. If it’s isosceles, two of the rectangles will be the same size. If it’s scalene, all three rectangles will be different. The formula still works, no matter what kind of triangle you’re dealing with!
Putting It All Together: The Grand Surface Area Equation
Now for the grand finale! To get the total surface area of the triangular prism, we just add up the area of the two triangles and the areas of the three rectangles:
Total Surface Area = (Area of two triangles) + (Area of Rectangle 1) + (Area of Rectangle 2) + (Area of Rectangle 3)
Let's substitute in our formulas:
Total Surface Area = (b * h) + (s1 * H) + (s2 * H) + (b * H)
You might see this written in a slightly different way too, which can be handy. Notice how `H` is in three of the terms? We can factor it out!
Total Surface Area = (b * h) + H * (s1 + s2 + b)

And what is `s1 + s2 + b`? That’s the perimeter of the triangular base! So, another way to think about it is:
Total Surface Area = (Area of two triangles) + (Perimeter of base * Height of prism)
This is a really useful way to remember and apply the formula. It’s like finding the area of the ends, then adding on the "wrap-around" area of the sides.
The Moment of Truth: Your Go-To Worksheet!
Okay, theory is great and all, but let’s get some practice in! Because let’s be honest, math is like riding a bike – you can read all about it, but you’ve gotta actually do it to get good. And that’s where our amazing surface area of triangular prism worksheet with answers PDF comes in.
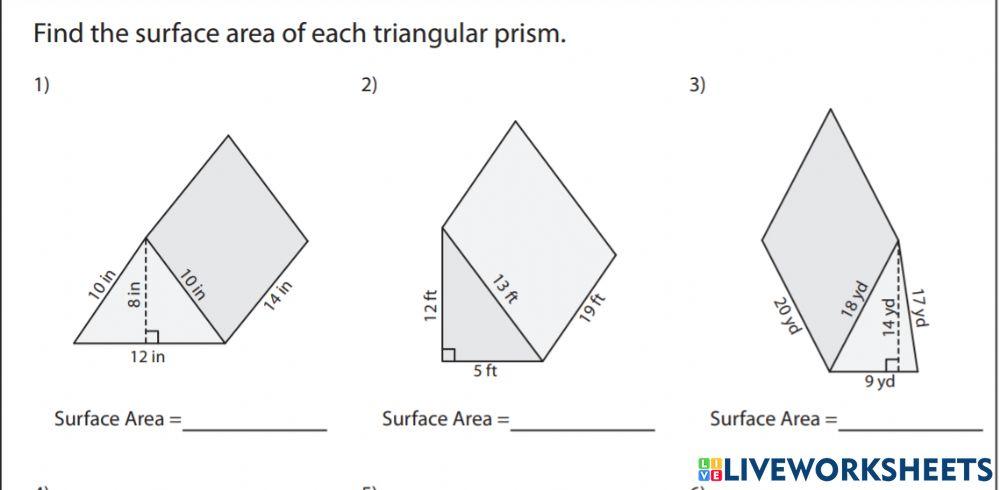
This worksheet is designed to be your best friend. It’s got a variety of problems, from super simple to a little bit more challenging, so you can build your confidence step-by-step. Each problem will give you the necessary dimensions for a triangular prism, and your mission, should you choose to accept it, is to calculate its total surface area.
What Makes Our Worksheet So Special?
We know there are tons of worksheets out there, so what makes ours stand out? Well, for starters:
- Clear and Concise Problems: No confusing jargon or unnecessarily complicated setups. Just straightforward geometric challenges.
- Variety of Triangles: You’ll encounter equilateral, isosceles, and scalene triangles, giving you a well-rounded practice experience.
- Accurate and Detailed Answers: This is the part you’ve been waiting for! The answer key is thorough. It doesn’t just give you the final number; it often shows you the step-by-step calculation, so you can see exactly how the answer was reached. This is crucial for learning and for spotting any little mistakes you might have made.
- PDF Format: Easy to download, easy to print, easy to use! No fuss, no muss. Just pure, unadulterated geometric problem-solving goodness.
- Fun Factor (Yes, Really!): We’ve tried to make the problems engaging. Maybe there’s a prism shaped like a slice of cheese, or a tent! Who knows? We believe that when you’re having a little fun, the learning sticks better.
Imagine this: you’re working through a problem, you get an answer, and you’re feeling pretty good. But then you check the answer key, and… gasp! It’s different. Instead of getting frustrated, you can look at the provided solution and go, "Ah! I see where I went wrong! I forgot to multiply by two for the bases!" This is the real magic of a good answer key – it’s a learning opportunity, not just a grading tool.

Tips and Tricks for Tackling the Worksheet
To make the most out of your worksheet experience, here are a few tips:
- Read Carefully: Make sure you understand which measurement is the base of the triangle, the height of the triangle, and the height of the prism. It’s amazing how often a small misinterpretation here can lead to a wonky answer.
- Draw a Picture: If the problem description is a bit abstract, sketch out the prism. Label all the sides and heights. This visual aid can be a lifesaver.
- Show Your Work: Even if you’re just doing it for yourself, write down each step of your calculation. This makes it so much easier to review your work and pinpoint any errors. Plus, when you’re checking against the answer key, you can compare your thought process.
- Use the Formula Consistently: Whether you prefer the expanded formula or the one with the perimeter, stick with it. Consistency reduces the chance of getting mixed up.
- Don’t Be Afraid to Revisit: If you find a particular type of problem tricky, don’t just skip it. Try it again, or look at the answer and work backward to see how they got there.
- Unit Awareness: Remember to keep track of your units (e.g., cm, inches, meters). Your final answer will be in square units (e.g., cm², inches², meters²).
And remember, if you’re stuck, that’s what the answer key is for! It’s not cheating; it’s smart learning. Think of it as having a patient tutor right there with you, ready to clarify things.
A Little Extra: Different Types of Triangular Prisms
Just a quick note to say that the formula we’ve discussed works for all types of triangular prisms. Whether the triangular base is:
- Right-angled: Where one of the angles in the triangle is 90 degrees.
- Equilateral: All three sides are the same length, and all angles are 60 degrees.
- Isosceles: Two sides are the same length, and the two angles opposite those sides are equal.
- Scalene: All sides and all angles are different.
The beauty of the formula is its universality! It’s like a magic spell that works on all prisms, regardless of their triangular quirks.
Beyond the Worksheet: Real-World Connections
So, you might be wondering, "When in my everyday life will I ever need to calculate the surface area of a triangular prism?" Well, you might be surprised!
- Architecture and Design: Think about roofs on houses that have a triangular shape (gable roofs). Knowing the surface area is important for calculating materials like roofing tiles or insulation.
- Packaging: As mentioned, some products come in triangular prism-shaped boxes. Manufacturers need to calculate surface area for material costs and design.
- Tent Manufacturing: Camping tents often have triangular prism shapes. This calculation is key for determining the amount of fabric needed.
- Art and Sculpture: Artists might use geometric shapes, including triangular prisms, in their work, and understanding surface area can be important for material selection and finishing.
So, it’s not just about passing a math test; it’s about understanding the world around you a little bit better. Pretty neat, huh?
Concluding with a Smile!
Alright, my geometrically inclined friend, you’ve made it to the end! We’ve journeyed through the fascinating world of triangular prisms, deciphered their surface area formulas, and armed you with a fantastic worksheet and its trusty answer key. Remember, the goal isn’t to memorize formulas until your brain feels like a wobbly Jell-O mold. The goal is to understand. To see how these shapes work, how their measurements fit together, and how we can use a little bit of math to quantify them.
Don't be discouraged if a problem feels tough at first. Every mathematician, from Newton to the person who invented the pizza box, started with the basics. So, embrace the challenge, use your worksheet as your guide, and celebrate every correct answer, no matter how small. You’re building a skill, and that’s something to be incredibly proud of. Go forth, calculate with confidence, and may your triangular prisms always have the perfect surface area!
