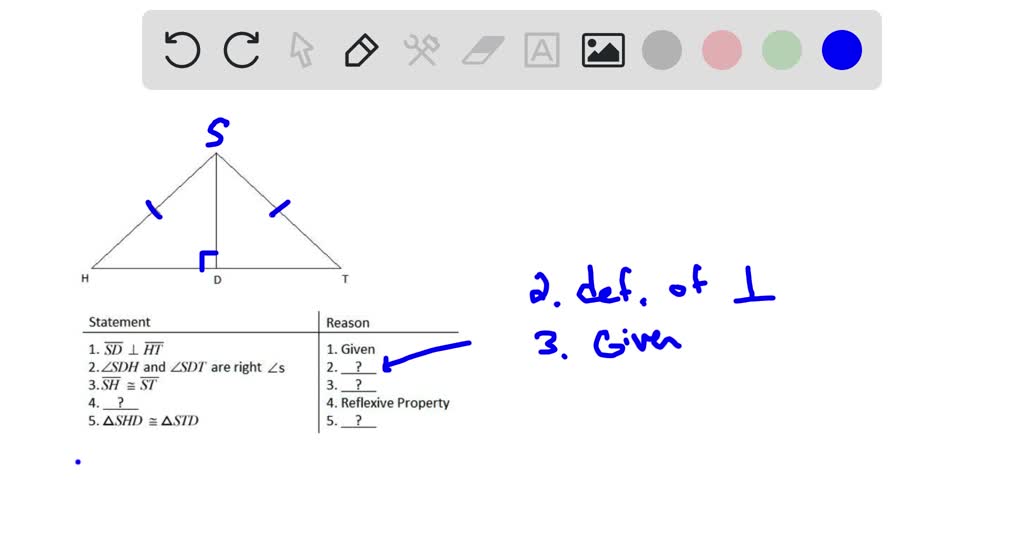
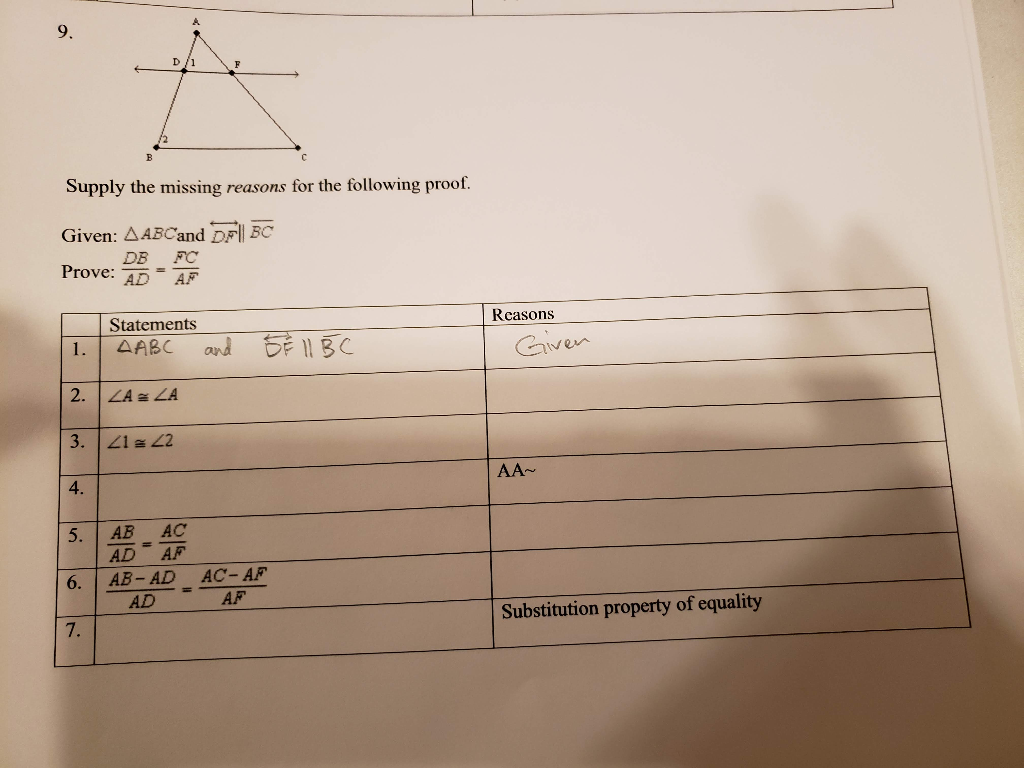
Supply The Missing Reasons To Complete The Proof

Hey there, fellow logic lovers! So, you know those moments when you're reading a mathematical proof, right? And it's all going swimmingly, step by step, like a well-oiled, super-smart machine. You're nodding along, feeling like a genius. Then BAM! Suddenly, there's a leap. A jump. A gaping chasm of... well, something that should totally be obvious, but for some reason, it's not. That, my friends, is what we're talking about today: the dreaded missing reason in a proof.
It's like you're on a treasure hunt, and the map suddenly goes blank in a crucial spot. You can see the next landmark, and you know you got there somehow, but the path? Poof! Vanished into thin air. Totally baffling, isn't it?
Sometimes, these missing reasons are so subtle, so tucked away, you start to question your own sanity. Are you missing something fundamental? Did you forget how to do basic arithmetic, or worse, basic logic? The existential dread can really set in, can't it?
And the authors! Oh, the authors of these proofs. They must be wizards, conjuring these logical leaps from thin air. Or perhaps they're just so deep in the mathematical forest, they can't see the trees. You know? They've been staring at this for so long, the obvious becomes invisible to them. It’s like trying to explain how to breathe to someone who’s always done it. “Uh, you just… inhale and… exhale?” Yeah, thanks for that, Einstein.
So, how do we, the mere mortals, bridge these gaps? How do we fill in those blank spaces and make the proof complete again? It’s a detective job, really. A mathematical Sherlock Holmes situation. You’ve got your clues (the given statements and previous steps), and you’ve got your mystery (the missing link). Time to put on your thinking cap!
First off, let's acknowledge the most common culprits. These are the usual suspects when it comes to those sneaky, unstated assumptions. Think of them as the silent partners in the proof. They’re there, making things happen, but they never quite get the spotlight.

The Usual Suspects: Unstated Assumptions
One of the biggest ones is often just basic arithmetic. I know, I know, it sounds ridiculous. But seriously, how many times have you seen something like, "Since 2 + 2 = 5, then QED"? Okay, maybe not that egregious, but you get the picture. They'll do a string of calculations, and then just present the final answer without showing the intermediate steps. And you’re left there, doing the math yourself, muttering, "Wait, where did that 7 come from? Oh, right, 3 times 2 is 6, plus 1 is 7. Of course!" It’s like they think we’re all walking calculators, ready to churn out the answers. Bless their hearts.
Then there's algebraic manipulation. Oh, the joys of rearranging equations! Sometimes, a proof will go from, "Let A = B" to "Therefore, 2A = 2B" without batting an eye. And you’re like, "Okay, but how did you get from A to 2A? Did you, like, multiply by two? On both sides? Is that even allowed?" The answer is, of course, yes, but sometimes they just… forget to mention it. It’s the property of equality, people! It’s not rocket science, but it sure can feel like it when it’s missing.
And let’s not forget geometric postulates and theorems. These are the bedrock of geometry proofs. Things like, "The sum of angles in a triangle is 180 degrees." Super important, right? But sometimes, a proof will just use that fact without explicitly stating, "By the Angle Sum Theorem for Triangles..." And you’re there, scrambling to remember which theorem allows you to make that jump. It’s like they assume you have a mental encyclopedia of every single geometrical truth ever discovered. Talk about pressure!
Another sneaky one is definitions. A definition is the most fundamental reason there is, right? If you say a shape is a "square," then by definition, it has four equal sides and four right angles. But in a proof, they might just assume you know that. They'll say, "Since ABCD is a square..." and then proceed to use properties that stem directly from the definition. You’re left thinking, "But why is it a square? What makes it a square?" The definition is the missing piece, the foundation upon which everything else is built.

And don’t even get me started on logical equivalences. This is where things can get really abstract. You'll have a statement, and then the next line will be something that looks completely different but is somehow supposed to be the same thing. Think about De Morgan's Laws, or the contrapositive. These are powerful tools, but if they’re not explicitly stated, you can feel like you’ve landed on another planet. "Wait, is 'not (A and B)' really the same as '(not A) or (not B)'? Are you pulling my leg?" Nope, just math.
The Art of Deduction: How to Fill the Gaps
So, how do we, as mere mortals, become proof-completing superheroes? It’s a learned skill, a bit of an art form, really. Here are some strategies to keep up your sleeve:
First, read very carefully. I know, I know, you’re already reading, but I mean really reading. Like, with a magnifying glass and a cup of strong coffee. Pay attention to every symbol, every word. Sometimes the missing reason is hidden in plain sight, disguised as a slightly rephrased version of something you’ve already seen.
Second, context is key. What chapter are you in? What topic is the proof about? If you're studying geometry, you can bet that the missing reason is probably a geometric theorem. If you're deep in set theory, it's likely a set operation or a set identity. The surrounding material is your most important clue.
Third, think about what needs to be true. Look at the statement you have and the statement you need to get to. What’s the logical connection? What established fact or rule would bridge that gap? It's like playing a game of connect-the-dots, but with theorems instead of dots.
Fourth, don't be afraid to use your own knowledge. If you know a certain theorem or property, even if it wasn't explicitly stated in your textbook, and it logically fits, then go for it! The proof is yours to complete, after all. It’s your chance to show off what you’ve learned. Be bold!
Fifth, try rephrasing. Sometimes, the reason is there, but it’s phrased in a way that’s just throwing you off. Try saying it out loud, or writing it in your own words. Does that spark any recognition? Does it sound like a familiar mathematical concept?
And of course, ask for help! Seriously. If you’ve tried everything and you’re still staring at a blank space, there’s absolutely no shame in asking a friend, a TA, or a professor. Sometimes, all it takes is a little nudge in the right direction. They’ve been there, they’ve felt your pain, and they can probably spot the missing reason in seconds.
The Joy of the "Aha!" Moment
Because let's be honest, there's nothing quite like that feeling when you finally figure out the missing reason. It's a tiny, glorious "Aha!" moment. A little spark of understanding that makes the whole proof click into place. It’s like finding the missing piece of a jigsaw puzzle, and suddenly, the whole picture makes sense. You feel so smart, so accomplished. You’ve conquered the proof!
It’s in those moments that the abstract beauty of mathematics really shines. It’s not just about rote memorization; it's about understanding the underlying logic, the elegant connections between ideas. When you can fill in those missing reasons, you’re not just completing a proof; you’re demonstrating a true grasp of the concepts.
So, the next time you encounter a proof with a mysterious gap, don't despair! Embrace the challenge. Channel your inner detective, dust off your logical reasoning skills, and go on a treasure hunt for that missing reason. It might be a frustrating journey at times, but the reward – that sweet, sweet "Aha!" moment – is absolutely worth it. Happy proofing, everyone!
