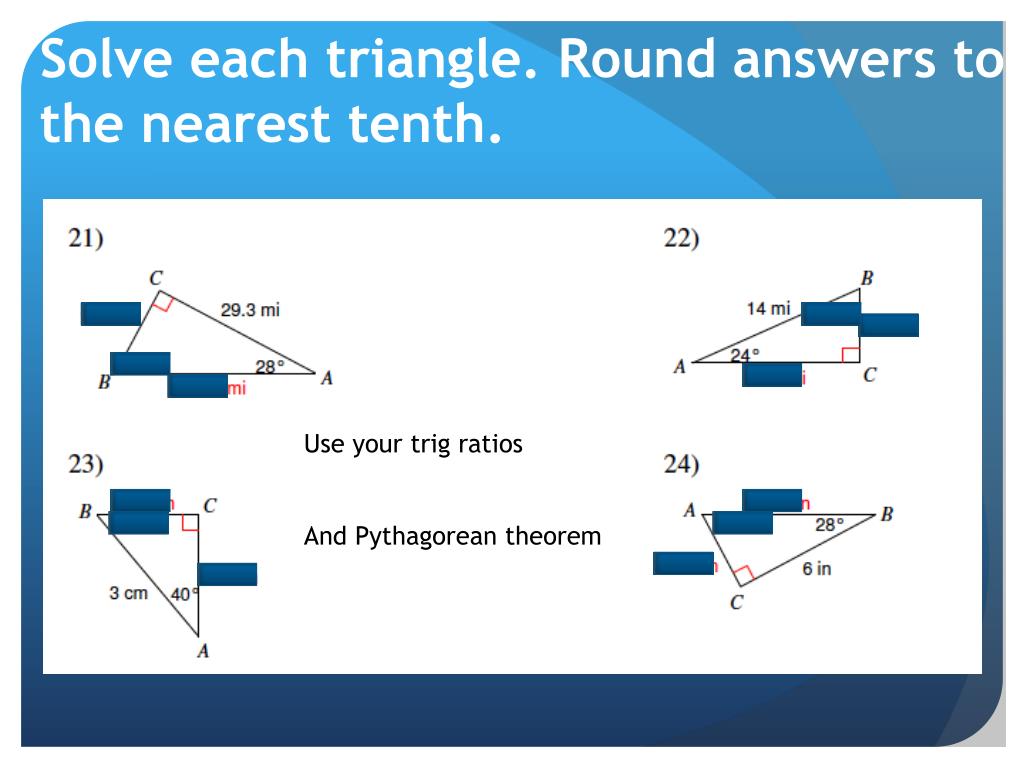
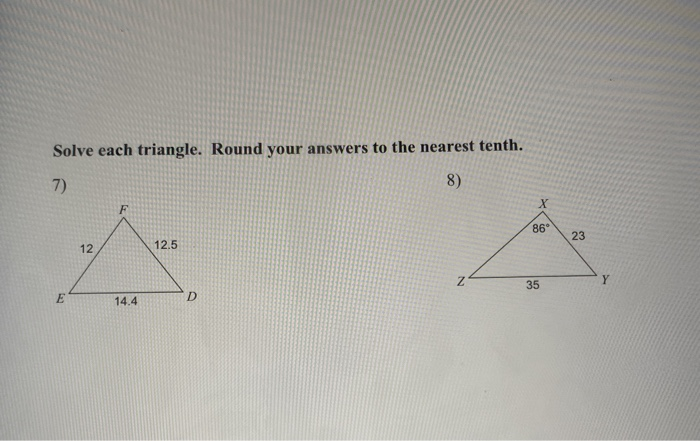
Solve Each Triangle Round Your Answers To The Nearest Tenth
Hey there, curious minds! Ever looked at a triangle and wondered, "What's its deal?" Like, beyond just being pointy? Well, buckle up, because we're about to dive into the surprisingly cool world of figuring out everything about a triangle. We're talking about solving it, which basically means finding all the missing pieces. Think of it like being a detective, but for shapes! And the best part? We're going to keep things chill, round our answers to the nearest tenth, and make this whole process feel less like a math test and more like a fun puzzle.
So, what exactly does it mean to "solve a triangle"? Imagine you have a triangle, but you only know a few things about it. Maybe you know two sides and the angle between them. Or maybe you know one side and two angles. There are different scenarios, kind of like different mystery novels. Your mission, should you choose to accept it, is to use the information you do have to figure out the lengths of the other sides and the measures of the other angles. Pretty neat, right?
Why is this even a thing? Well, it turns out triangles are everywhere! They're the backbone of so many things we use and see every day. Think about construction – building bridges, roofs, even the frame of a house. Triangles are incredibly stable. Surveyors use them to measure distances and plot land. Sailors and pilots navigate using triangles. Even in computer graphics, triangles are fundamental for creating 3D models. So, understanding triangles isn't just some abstract math exercise; it's a practical skill that helps us understand and build the world around us. It's like learning a secret code for the physical world!
The Tools of the Trade: Your Triangle-Solving Toolkit
To solve a triangle, we need a few trusty tools. Don't worry, they're not complicated, just really helpful. The two main heroes of our story are the Law of Sines and the Law of Cosines. You can think of these as super-powered versions of the Pythagorean theorem, which you might remember from school (a² + b² = c², for those right-angled triangles). The Pythagorean theorem only works for right triangles, but the Law of Sines and Cosines? They work for any triangle. That's a game-changer!
The Law of Sines is pretty straightforward. It basically says that the ratio of the length of a side of a triangle to the sine of its opposite angle is constant for all three sides. So, if you have side 'a' and its opposite angle 'A', side 'b' and its opposite angle 'B', and side 'c' and its opposite angle 'C', then a/sin(A) = b/sin(B) = c/sin(C). See? It connects sides and angles in a beautiful, proportional way. It's like finding a consistent relationship in a crowd of people – no matter who you pick, the connection between their height and the angle you're looking at them from (weird analogy, I know, but stick with me!) remains the same.

Then there's the Law of Cosines. This one's a bit more involved but equally powerful. It's like the Law of Sines' more sophisticated cousin. It relates the lengths of the sides of a triangle to the cosine of one of its angles. For example, to find side 'c', you can use c² = a² + b² - 2ab * cos(C). Notice how it looks a little bit like the Pythagorean theorem (a² + b²), but then it has that extra bit with the cosine? That extra bit is what makes it work for non-right triangles. It's like adding a special adjustment factor to account for the "slantiness" of the triangle.
Let's Get Solving! Different Scenarios, Different Strategies
Now, how do we actually use these laws? It depends on what information you're given. Think of it like having a partially filled-in crossword puzzle. You need to look at the clues you have to figure out which letters go where.

Scenario 1: Angle-Side-Angle (ASA) or Angle-Angle-Side (AAS)
If you know two angles and the side in between them (ASA), or two angles and a side that's not between them (AAS), you're in a pretty good spot. Why? Because the angles in any triangle always add up to 180 degrees. So, if you know two angles, you can instantly find the third angle! Boom! Just like that. Then, you've got three angles and one side. Now, the Law of Sines is your best friend. You can set up your ratios and solve for the missing sides. It's like having a key piece of information that unlocks the rest of the puzzle.
Let's say you have angle A, angle B, and side c. You can find angle C (180 - A - B). Then, using the Law of Sines: a/sin(A) = b/sin(B) = c/sin(C). You can pick one of those equalities (e.g., a/sin(A) = c/sin(C)) and solve for the unknown side 'a'. Repeat for side 'b'. Easy peasy, right? We're just being systematic. Rounding to the nearest tenth as we go, of course, so our answers are nice and tidy.
![[ANSWERED] Solve each triangle Round your answers to the nearest tenth](https://media.kunduz.com/media/sug-question-candidate/20230219220341443966-5385667.jpg?h=512)
Scenario 2: Side-Side-Side (SSS)
What if you know all three sides (SSS)? This is where the Law of Cosines shines. You can use it to find any of the angles. For instance, if you know sides a, b, and c, you can rearrange the Law of Cosines to solve for cos(C): cos(C) = (a² + b² - c²) / 2ab. Once you have the cosine of the angle, you can use the inverse cosine function (often written as cos⁻¹ or arccos on your calculator) to find the angle itself. Again, round to the nearest tenth!
Once you find one angle using the Law of Cosines, you've got three sides and one angle. Now, the Law of Sines can be your go-to for finding the remaining two angles. Just be a little careful here. Sometimes, with the Law of Sines, you can run into an "ambiguous case" where there might be two possible triangles. However, with SSS, you're guaranteed to have just one unique triangle. Phew! It's like knowing you're building a specific Lego set – all the pieces fit perfectly and there's only one way to put them together.
Scenario 3: Side-Angle-Side (SAS)
This one's a bit like a surprise ingredient in a recipe. You know two sides and the angle between them (SAS). Your first move here is to use the Law of Cosines to find the side opposite the known angle. For example, if you have sides 'a' and 'b' and the angle 'C' between them, you'd use c² = a² + b² - 2ab * cos(C) to find side 'c'. Once you've found that third side, you suddenly have an SSS situation! Congratulations, you've just transformed the problem. Now you can use the Law of Sines (or even the Law of Cosines again, if you prefer) to find the remaining two angles. It's like starting with a puzzle piece and then using it to reveal the next set of clues.
Why Does Rounding to the Nearest Tenth Matter?
You might be asking, "Why the fuss about rounding to the nearest tenth?" Think of it like precision in real life. We don't usually need to know a length to a million decimal places. For most practical applications, like building a shelf or plotting a course, a tenth of a unit (whether it's an inch, a centimeter, or a nautical mile) is perfectly fine. It keeps our numbers manageable and makes our answers more user-friendly. It's like saying "about 5 feet tall" instead of "5.00032 feet tall." We're aiming for practical accuracy. Plus, it makes the calculations a bit cleaner, so we can focus on the cool geometry!
So, there you have it! Solving triangles might sound daunting at first, but with the Law of Sines and the Law of Cosines as your trusty sidekicks, it's a really rewarding process. It’s about piecing together information, seeing how different parts of a shape relate to each other, and ultimately, understanding the world a little bit better. So next time you see a triangle, don't just see a pointy shape. See a puzzle waiting to be solved, a secret waiting to be revealed. Happy triangle-solving!
