Secondary Math 3 Module 3 Polynomial Functions Answer Key

Okay, so let's talk about something that might sound a tad intimidating at first glance: Secondary Math 3 Module 3 Polynomial Functions Answer Key. Now, before you start picturing your high school math teacher frantically scribbling equations on a chalkboard while simultaneously juggling textbooks (which, let's be honest, is a vivid image for many of us), take a deep breath. This isn't about memorizing arcane formulas that you'll never, ever use again. This is about understanding how things grow, how they curve, and how they make sense of the world around us. Think of it like figuring out the secret sauce behind everything from baking a perfect cake to predicting the trajectory of a rogue frisbee.
Seriously, polynomial functions are everywhere. They're the silent architects of our everyday experiences, and the answer key? Well, that's just your friendly neighborhood guide to making sure you're on the right track. It's like having the cheat sheet for life's more complicated recipes, or the user manual for that ridiculously complex IKEA furniture you bravely decided to assemble.
Let's break down what we're even talking about. A "polynomial function" sounds fancy, right? Like something a wizard would conjure up. But at its core, it's just a way to describe relationships where things aren't necessarily linear. Think about a straight line. That's simple. You go up one step, you go over one step, and it's always the same. Predictable. Like a perfectly behaved cat.
But life, my friends, is rarely a straight line. It's more like a rollercoaster! Sometimes things go up really fast, then they level off, then they dip, and then they soar again. That, my darlings, is a polynomial function at play. Imagine you're trying to figure out how much your savings account grows over time. It's not just adding the same amount each month (that would be linear). Interest compounds, right? So it starts slow, then picks up speed. Or maybe you're launching a rocket (or, you know, a water balloon from your upstairs window). The path it takes isn't a straight shot. It curves, it arcs, it eventually comes down. All thanks to the magic of polynomials!
So, what about this "Secondary Math 3 Module 3" thing? Think of it as a specific chapter in your educational adventure, focusing on these curvier, more exciting relationships. And the "Answer Key"? This is where the real joy begins, if you're anything like me. It's the moment of truth. Did you nail it? Did you accidentally invent a new mathematical paradox? The answer key is there to gently nudge you in the right direction, or, more importantly, to give you that satisfying aha! moment when you realize you totally understood it.
The "Why Bother?" Behind Polynomials
You might be asking, "Why should I care about polynomial functions?" Great question! It's the same question I used to ask about why I needed to know how to fold a fitted sheet properly. Turns out, both have their surprisingly practical applications. Polynomials are the backbone of so many things we take for granted. Think about the graphics on your favorite video game. Those smooth, curved surfaces? Polynomials. The way weather patterns are modeled? You guessed it, polynomials. Even the way a chef designs a menu to maximize profits can involve polynomial equations.

It’s like understanding why your bread rises. You don’t need to be a chemist to appreciate a fluffy loaf, but knowing a little about yeast and fermentation helps you get a better loaf. Polynomials are that little bit of extra insight into the "how" and "why" of things that move and change in more complex ways.
Consider this: You're baking cookies. The recipe calls for a certain amount of flour, sugar, and butter. If you double the recipe, you double the ingredients, right? That's linear. But what happens if you're trying to figure out the perfect oven temperature and baking time to get that ideal crispy-chewy balance? That's not a straight-line relationship. Too hot, and they burn. Too cool, and they're pale and sad. There's a sweet spot, a curve, an optimal point, and polynomial functions help us find that. It’s the difference between a decent cookie and a cookie that makes your neighbors jealous.
The Answer Key: Your Trusty Sidekick
Now, let's get to the star of our show, the illustrious Secondary Math 3 Module 3 Polynomial Functions Answer Key. Imagine you've just spent an hour wrestling with a particularly gnarly problem. You've drawn diagrams, you've scribbled notes, you've possibly even consulted a wise elder (or Google). You're pretty sure you've got it, but there's that tiny nagging doubt. Did you carry the one? Did you forget to square something? Did you accidentally divide by zero and create a black hole in your notebook?
The answer key is your superhero cape. It swoops in and says, "Fear not, brave mathematician! Let's see how you did." It's not about judging you; it's about guiding you. It's like having a friend who's already taken the test and is saying, "Yeah, you're on the right track with that!" or "Oops, remember to distribute that negative sign, it's a sneaky one!"
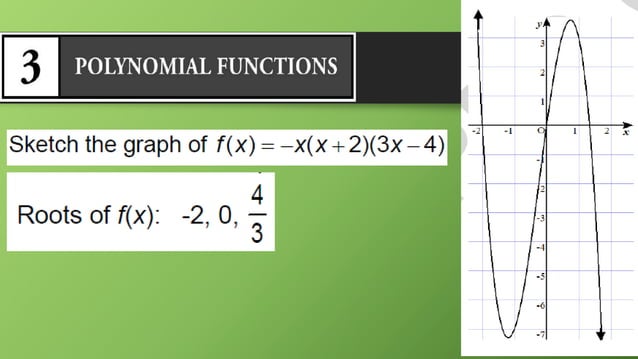
Think of it like assembling furniture with those notoriously vague instruction manuals. You're plugging along, feeling pretty confident, and then you hit a step that makes absolutely no sense. The answer key is like finding a picture of the finished product online, or a step-by-step video tutorial. It clarifies the confusion, confirms your progress, and helps you avoid that sinking feeling of realizing you've attached the left leg to the ceiling.
And let's be honest, sometimes the biggest relief is just knowing you're not completely off your rocker. When you've painstakingly worked through a problem and the answer key confirms your result, there's a little dopamine hit. It's a confirmation that your brain, that magnificent, sometimes-frustrating organ, is actually capable of understanding this stuff. It's a high-five to yourself.
Common Pitfalls (and How the Answer Key Saves the Day)
Polynomials can have their quirks. You've got degrees, coefficients, terms, and all sorts of fancy names for the bits and pieces. And then there are the operations: addition, subtraction, multiplication, and – oh boy – division. Division by polynomials? That can feel like trying to untangle a headphone cord that's been in your pocket for a week.

One common pitfall is with the exponents. Sometimes, you forget to add them when multiplying, or you subtract them incorrectly when dividing. It's like forgetting to add the baking powder to your cake – the results are usually not ideal. The answer key, in these moments, is your vigilant guardian. It will clearly show the correct exponent manipulation, and you can go back and say, "Ah, that's where I went wrong!" It's a learning opportunity, not a failure.
Another fun one is dealing with negative signs. They're like gremlins in the math world. They can pop up unexpectedly and turn your perfectly good answer into something completely different. When you're distributing a negative sign across multiple terms, it's easy to miss one. The answer key is there to catch those rogue negatives and show you the proper way to herd them into submission. It's like having a dog walker who makes sure all the puppies are accounted for.
Factoring can also be a beast. Trying to break down a complex polynomial into its simpler parts can feel like trying to solve a Rubik's Cube blindfolded. There are different methods, and sometimes you just can't see the right combination. The answer key will present the factored form, and then you can work backward, or at least appreciate the elegance of the solution and understand the steps involved in getting there. It's like seeing the finished masterpiece and then learning about the techniques the artist used.
Beyond the Classroom: Where Polynomials Live
The beauty of understanding polynomial functions, and having that handy answer key to guide you, is that it opens your eyes to the world around you. Suddenly, you're not just seeing shapes; you're seeing the mathematical principles behind them.

Imagine you're driving. The speedometer shows you your speed, which is often changing. The way your car accelerates or brakes isn't always a steady, constant rate. It’s often described by polynomials, allowing engineers to design smoother, more efficient rides. That gentle curve you feel as your car picks up speed? Polynomials at work!
Or think about finance. The growth of investments, the depreciation of assets, loan amortization – all these involve calculations that often go beyond simple interest. Polynomial functions help model these complex financial landscapes, allowing for more accurate predictions and better financial planning. It's the math behind how your money actually works, not just the simplistic version you might learn on day one.
Even in medicine, polynomials are used. Drug dosages, the spread of diseases, and the analysis of medical imaging can all involve polynomial models. It’s about understanding how things change and evolve over time, and polynomials are a powerful tool for that. So, the next time you're feeling a bit lost in those polynomial functions, remember you're not just doing math homework; you're gaining a deeper understanding of the world, from the curve of a baseball's flight to the intricate workings of our economy.
And the answer key? It's just your trusty guide, your friendly companion on this journey of discovery. It’s there to reassure you, to clarify, and to celebrate your successes. So, embrace the polynomials, use that answer key wisely, and go forth and understand the beautiful, complex, and often curved world around you!
