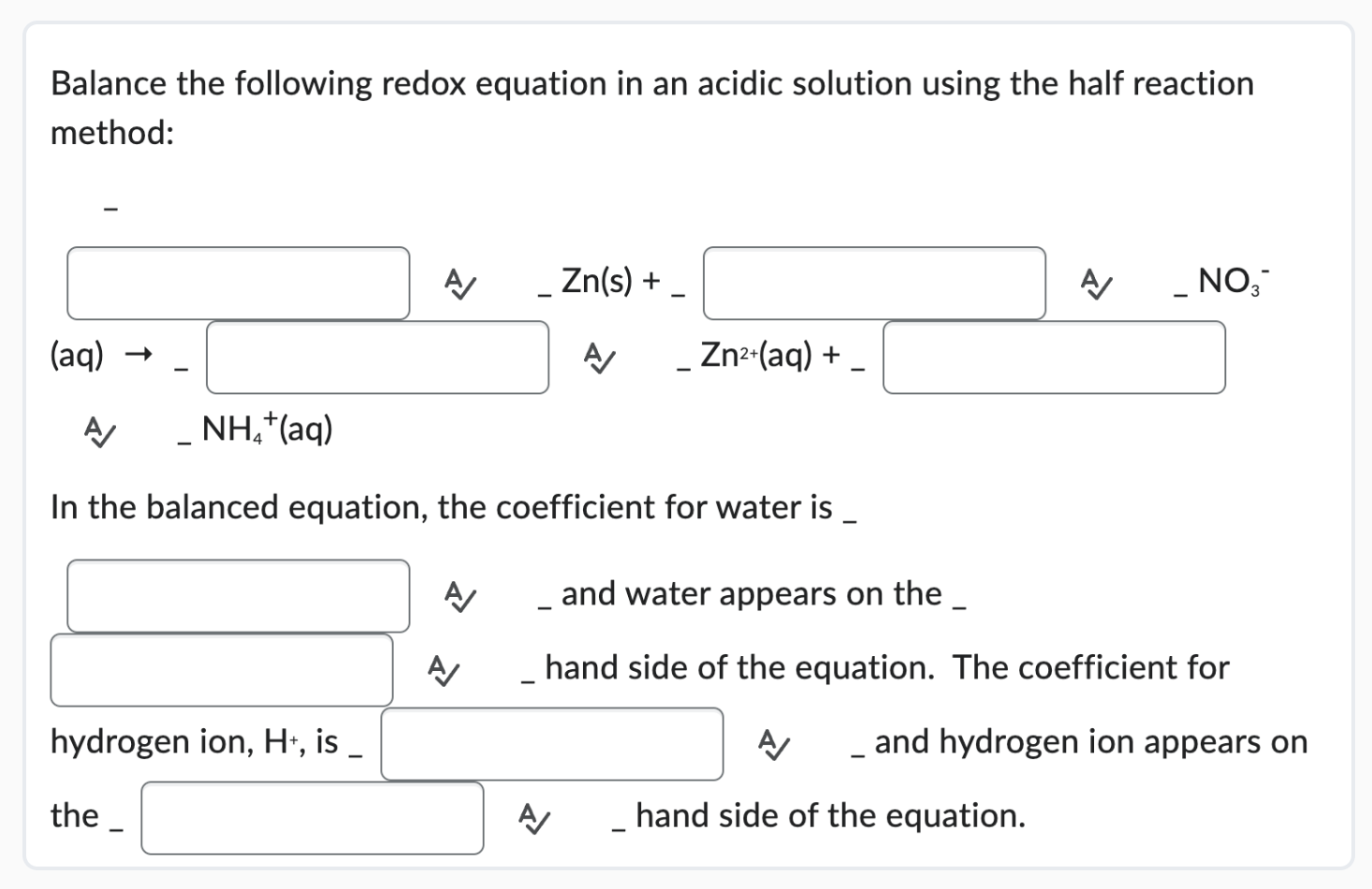
Provide The Coefficients Needed To Balance The Redox Reaction Given.

Hey there, science adventurers! Ever stared at a chemical equation and felt like you needed a secret decoder ring just to figure it out? Especially when it's one of those redox reactions? Don't sweat it! We're about to dive into the wonderfully weird world of balancing these beasts, and I promise, it's going to be way more fun than a root canal. Think of me as your friendly neighborhood chemical equation whisperer, here to make balancing feel less like a chore and more like a delightful puzzle.

So, what’s the big deal with redox reactions anyway? Basically, they're all about electron tango. One thing loses electrons (gets oxidized, think of it as getting a bit extra), and another thing gains them (gets reduced, it's chilling out, becoming less). It’s a whole give-and-take situation, and just like a perfectly choreographed dance, everything needs to be in balance. If one partner is doing too much electron-flinging, the other needs to be ready to catch them!

The challenge often comes when we're given an equation that looks like a spaghetti explosion of atoms. They're all there, but they're not in the right proportions. Our job is to find the magic numbers – the coefficients – that make everything click. These little guys go in front of the chemical formulas, like bouncers at a club, ensuring that the number of atoms of each element is the same on both sides of the reaction arrow. Pretty neat, huh?

Now, the prompt is asking us to provide the coefficients needed to balance a specific redox reaction. Since the reaction itself isn't explicitly given here, let's imagine we're tackling a classic. How about the reaction between permanganate ion ($MnO_4^-$) and iron(II) ions ($Fe^{2+}$) in an acidic solution? This one's a real crowd-pleaser in chemistry labs, and it’s a fantastic example for practicing our balancing skills. Don't worry, we'll break it down step-by-step, like we're building a really awesome LEGO castle.

The unbalanced equation for our imaginary scenario looks something like this: $MnO_4^- + Fe^{2+} \rightarrow Mn^{2+} + Fe^{3+}$. See? Permanganate is looking a bit grumpy, and iron(II) is feeling a little less positive. But by the end, iron becomes iron(III) (more positive, more electrons gone!), and manganese in permanganate becomes manganese(II) (less positive, electrons gained!). It’s a chemical transformation worthy of a superhero origin story!

The easiest way to tackle these is the half-reaction method. It sounds fancy, but it’s just splitting the big, scary reaction into two smaller, more manageable ones: one for oxidation and one for reduction. It’s like dividing a huge task into two bite-sized chunks. You wouldn't try to eat an entire pizza in one go, right? Same principle!

Let's find our oxidation half-reaction first. We see that iron(II) ($Fe^{2+}$) is turning into iron(III) ($Fe^{3+}$). This is where the electrons are getting liberated. The iron atom is losing an electron. To balance this little guy, we write: $Fe^{2+} \rightarrow Fe^{3+}$. Now, we need to make sure the charge is balanced. On the left, we have a +2 charge. On the right, we have a +3 charge. To fix this, we need to add an electron ($e^-$) to the right side. So, our balanced oxidation half-reaction is: $Fe^{2+} \rightarrow Fe^{3+} + e^-$. Ta-da! The charge is now +2 on both sides. Easy peasy lemon squeezy!

Next up is the reduction half-reaction. This is where the electrons are being snagged. We've got permanganate ($MnO_4^-$) turning into manganese(II) ($Mn^{2+}$). This one's a bit more involved, but we’ve got this! Let's start with the atoms that aren't oxygen or hydrogen: $MnO_4^- \rightarrow Mn^{2+}$. The manganese atoms are already balanced (one on each side). Nice start!

Now, let's deal with the oxygen. We have four oxygen atoms on the left and none on the right. To balance oxygen, we add water ($H_2O$) molecules. We need four water molecules on the right side: $MnO_4^- \rightarrow Mn^{2+} + 4H_2O$. See? We've added oxygen, but we've also added hydrogen. Uh oh, more balancing!

Now for the hydrogen. We have 8 hydrogen atoms on the right (from the four water molecules) and none on the left. In acidic solutions, we balance hydrogen by adding hydrogen ions ($H^+$). We need 8 hydrogen ions on the left: $MnO_4^- + 8H^+ \rightarrow Mn^{2+} + 4H_2O$. Looking good!

Finally, the charge balance for our reduction half-reaction. On the left side, we have a charge of (-1) from $MnO_4^-$ and (+8) from the 8 $H^+$, making a total of +7. On the right side, we have a charge of (+2) from $Mn^{2+}$ and (0) from the water. To make the charges equal, we need to add electrons ($e^-$) to the side with the higher positive charge (the left side). We need 5 electrons to go from +7 to +2. So, our balanced reduction half-reaction is: $MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O$. We've done it! The charge is +2 on both sides. High fives all around!

Now, we have our two balanced half-reactions: 1. Oxidation: $Fe^{2+} \rightarrow Fe^{3+} + e^-$ 2. Reduction: $MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O$

The tricky part is that the number of electrons lost in the oxidation must equal the number of electrons gained in the reduction. In our oxidation half-reaction, we're losing 1 electron. In our reduction half-reaction, we're gaining 5 electrons. They're not playing on the same team yet!

To fix this, we need to find the least common multiple of 1 and 5, which is, you guessed it, 5! We need to multiply the entire oxidation half-reaction by 5 so that it also involves 5 electrons. And the reduction half-reaction? It already has 5 electrons, so we can multiply it by 1 (which means we just leave it as is). It’s like getting both sides of the equation to speak the same electron language.

So, let's multiply our oxidation half-reaction by 5: $5 \times (Fe^{2+} \rightarrow Fe^{3+} + e^-)$ becomes $5Fe^{2+} \rightarrow 5Fe^{3+} + 5e^-$. And our reduction half-reaction stays the same: $MnO_4^- + 8H^+ + 5e^- \rightarrow Mn^{2+} + 4H_2O$.

Now, notice the 5 electrons ($5e^-$) on the product side of the oxidation and the 5 electrons ($5e^-$) on the reactant side of the reduction. Since electrons are neither created nor destroyed in the overall reaction, they cancel each other out when we combine the two half-reactions. Poof! Gone!

Let's combine everything, bringing all the reactants to one side and all the products to the other, and then crossing out those electrons: $(5Fe^{2+}) + (MnO_4^- + 8H^+ + 5e^-) \rightarrow (5Fe^{3+} + 5e^-) + (Mn^{2+} + 4H_2O)$

Cancel out the $5e^-$ on both sides:

$5Fe^{2+} + MnO_4^- + 8H^+ \rightarrow 5Fe^{3+} + Mn^{2+} + 4H_2O$

And there you have it! Our beautifully balanced redox equation. The coefficients we needed are: * For $Fe^{2+}$: 5 * For $MnO_4^-$: 1 (we usually don't write the '1' coefficient, but it's there!) * For $H^+$: 8 * For $Fe^{3+}$: 5 * For $Mn^{2+}$: 1 * For $H_2O$: 4

Let's do a quick check to make sure all the atoms and charges are balanced. On the reactant side: * Fe: 5 * Mn: 1 * O: 4 * H: 8 * Total charge: $5(+2) + (-1) + 8(+1) = +10 - 1 + 8 = +17$ On the product side: * Fe: 5 * Mn: 1 * O: 4 * H: 8 * Total charge: $5(+3) + (+2) + 4(0) = +15 + 2 + 0 = +17$

Everything matches! We've successfully navigated the currents of electron transfer and emerged victorious. Isn't that a fantastic feeling? It's like solving a really tricky Sudoku or finally understanding that complex song lyrics. You put in the effort, you break it down, and then... aha! It all makes sense.

Remember, balancing redox reactions is a skill that gets better with practice. Don't get discouraged if it feels a little wobbly at first. Every time you tackle one, you’re strengthening your chemical intuition. You're learning to see the flow of electrons, the dance of the atoms, and the beauty of a balanced equation. So, the next time you see one of these challenging reactions, just take a deep breath, remember our little step-by-step guide, and embrace the puzzle. You've got the power to make those electrons behave!

And hey, if you ever get stuck, just imagine me cheering you on from the sidelines, maybe with a little cowbell and a "You got this!" banner. Because in the grand, exciting world of chemistry, you absolutely do. Keep exploring, keep questioning, and keep balancing. The universe of molecules is waiting for your brilliant touch!