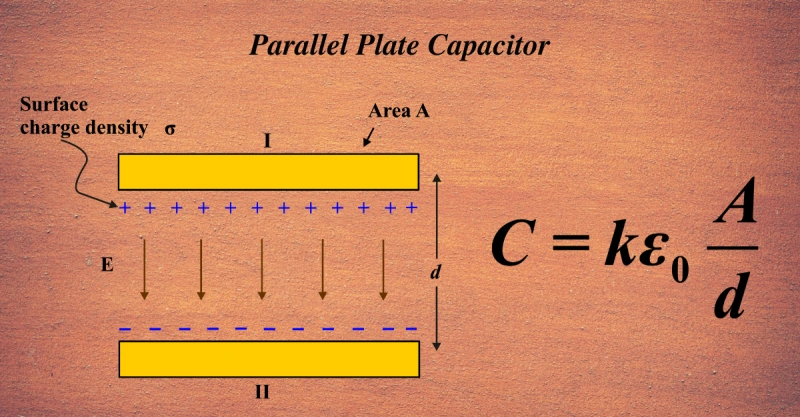
Predict The Change In Capacitance Of A Parallel Plate Capacitor

Ever wonder what makes your smartphone’s touchscreen so responsive, or how those tiny capacitors in your electronic gadgets store energy? It’s all thanks to a clever little device called a parallel plate capacitor! And the really fun part? We can actually predict how its ability to store charge – its capacitance – will change. It’s like having a superpower to understand and even tweak the heart of so many modern technologies. Forget dusty textbooks; we’re diving into the exciting world of electronics where a simple tweak can lead to big results!

Why Predicting Capacitance is a Big Deal

So, why should you care about predicting capacitance changes? Think of it as the secret sauce that allows engineers to design everything from the flash on your camera to the complex circuits in a high-speed computer. Knowing how capacitance behaves under different conditions is absolutely crucial. It allows us to:

• Optimize performance: We can fine-tune devices for faster charging, better signal reception, and longer battery life.
• Ensure reliability: By understanding how factors like temperature or material changes affect capacitance, engineers can build devices that work consistently and don’t fail unexpectedly.
• Innovate and miniaturize: Predicting capacitance helps us shrink components while maintaining or even improving their functionality. This is key for making our gadgets smaller, lighter, and more powerful.
• Troubleshoot problems: If a device isn’t working as expected, understanding capacitance changes can help pinpoint the issue.

In essence, predicting capacitance change is the bedrock of electrical engineering. It’s about understanding the fundamental principles that power our digital lives. It’s not just about theory; it’s about making things work better, faster, and more reliably. Pretty cool, right?

The Magic Formula: Unpacking the Basics

At its core, a parallel plate capacitor is surprisingly simple. Imagine two flat metal plates placed very close to each other, but not touching. When you apply a voltage across these plates, electrical charge builds up on them – positive on one, negative on the other. This separation of charge is what allows the capacitor to store energy. The amount of charge it can store for a given voltage is its capacitance, measured in farads.

Now, here’s where the prediction magic comes in. The capacitance of a parallel plate capacitor isn’t just a fixed number; it can change! The key players that influence capacitance are:

• The area of the plates (A): The larger the plates, the more charge they can hold. Think of it like having a bigger bucket for water.
• The distance between the plates (d): The closer the plates are, the stronger the electric field between them, allowing them to store more charge. It’s like squeezing more energy into a smaller space.
• The material between the plates (the dielectric): This is perhaps the most fascinating factor. The material sandwiched between the plates, called the dielectric, plays a huge role. Different materials have different abilities to polarize (their internal charges shifting in response to the electric field), which enhances the capacitor’s ability to store charge.

The fundamental formula that ties these together is:

Capacitance of Parallel Plate Capacitor with a Conducting Slab

C = (ε₀ * εᵣ * A) / d

Let’s break down this elegant equation:

• C is, of course, our capacitance.
• ε₀ (epsilon-naught) is a fundamental constant called the permittivity of free space. It’s a universal number that tells us how easily electric fields can pass through a vacuum.
• εᵣ (epsilon-r) is the relative permittivity, also known as the dielectric constant, of the material between the plates. This is the superstar that we can change! A vacuum has an εᵣ of 1. Most common materials have εᵣ values greater than 1. For example, air has an εᵣ close to 1, while materials like mica or certain ceramics can have εᵣ values in the tens, hundreds, or even thousands!
• A is the area of one of the plates.
• d is the distance between the plates.

See how εᵣ is multiplied in the numerator? This means a higher dielectric constant directly leads to higher capacitance. It’s the secret ingredient for making capacitors more potent!

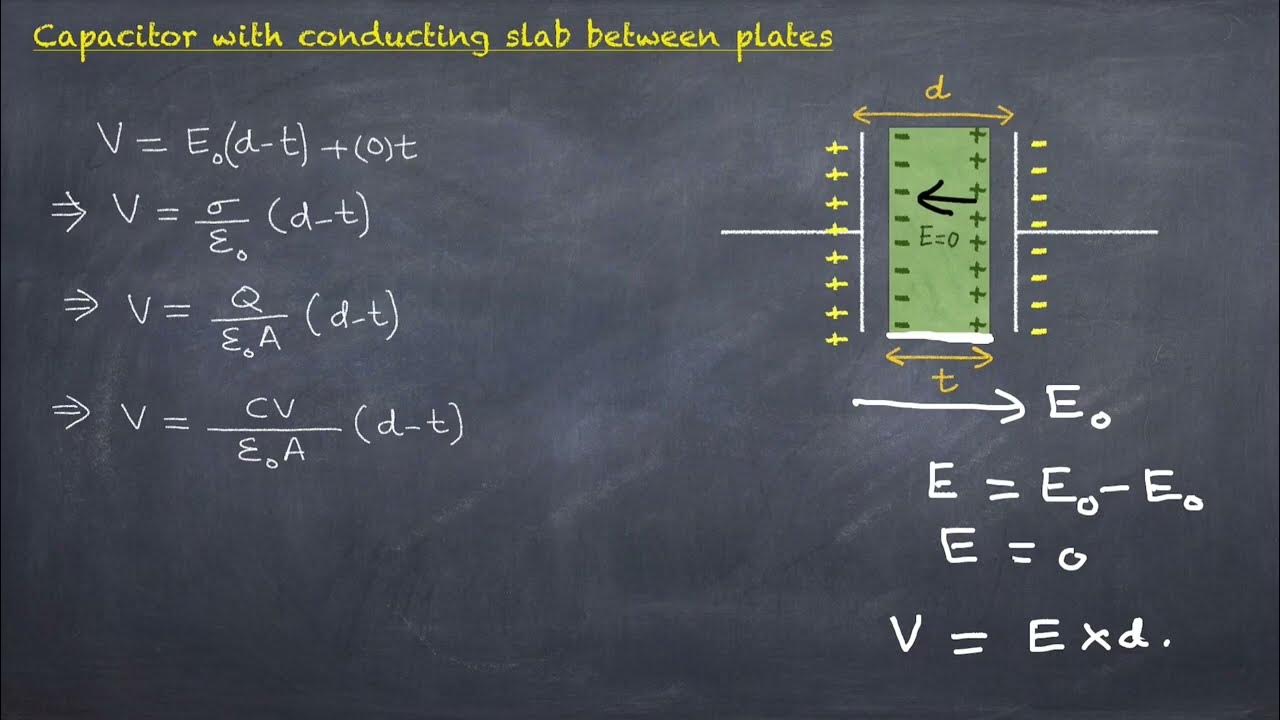
Predicting the Change: What Happens When We Tweak?

Now for the fun part – predicting what happens when we change things!

Capacitance of Parallel Plate Capacitor with Dielectric Slab

1. Changing the Area (A):

If we increase the area of the plates, say by making them wider or longer, our capacitance will increase proportionally. The formula shows that C is directly proportional to A. So, double the area, and you roughly double the capacitance, assuming everything else stays the same. This is a straightforward way to boost a capacitor's storage capacity.

2. Changing the Distance (d):

Conversely, if we decrease the distance between the plates, the capacitance increases. The formula tells us that C is inversely proportional to d. Halving the distance between the plates will double the capacitance. This is why capacitor designs often strive for incredibly thin dielectric layers – every micrometer counts!

PPT - Understanding Capacitors and Capacitance in Electronics

3. Changing the Dielectric Material (εᵣ):

This is where things get really interesting! By swapping out the material between the plates, we can dramatically alter the capacitance. If we replace the air (εᵣ ≈ 1) with a material that has a dielectric constant of, say, 100, our capacitance will jump by a factor of 100! This is how engineers pack so much energy storage into tiny spaces. Different dielectric materials are chosen for specific applications – some offer high capacitance, others offer better insulation, and some can withstand high temperatures or voltages.

Combining Changes:

3. A parallel plate capacitor of capacitance | StudyX

The real power comes when we combine these changes. Imagine you have a capacitor with a certain area and distance, filled with air. You can then:

• Increase its capacitance by bringing the plates closer together.
• Increase its capacitance further by using a material with a higher dielectric constant instead of air.
• Maximize capacitance by using large plates, very close together, with a high-dielectric-constant material.

Other Factors (for the curious!)

While the basic formula covers the most significant changes, in real-world applications, other factors can also influence capacitance, though often to a lesser extent. These include:

• Temperature: The dielectric constant of many materials changes with temperature, so capacitance can vary accordingly.
• Voltage: For some dielectric materials, the dielectric constant can slightly change at very high voltages.
• Frequency: In AC circuits, the dielectric’s response can lag behind the changing electric field at very high frequencies.

Understanding these fundamental relationships allows us to predict, design, and innovate. Whether you’re building a powerful new electronic device or just trying to understand how your existing gadgets work, the principles of parallel plate capacitance are your gateway to a fascinating world. It’s a beautiful blend of simple geometry and material science that powers our modern lives!