Points Distance And Line Segments Common Core Geometry Homework

Hey there, geometry gurus and geometry… um, beginners! So, your homework has dropped, and it’s all about points, distance, and line segments. Sounds a little intimidating, right? Like a secret code only mathematicians understand? Nah, think of it more like unlocking a cool, visual puzzle. We’re going to break this down, and I promise it won't be more painful than trying to assemble IKEA furniture without the instructions.

First things first, let’s talk about our foundational building blocks: points. What even is a point? Imagine the tiniest speck you can possibly think of. So small you can’t divide it further. That’s a point! It has no size, no length, no width, no height. It’s just… a location. We usually draw them as little dots, and we give them fancy capital letters, like point A, point B, or even point Schrödinger (don't ask, it's a long story involving a cat and quantum physics, probably not on your homework). These little dots are the absolute bedrock of geometry. Without them, we'd just be floating in a void of… well, nothingness. And that’s no fun for anyone!

Now, what can we do with these lonely little points? We can connect them! And when we connect two points, we create something super important: a line segment. Think of it as a straight road connecting two cities. It has a definite beginning and a definite end. It’s not an endless highway that goes on forever; it’s a specific stretch. We represent a line segment by the two points it connects. So, if you connect point P and point Q, you’ve got line segment PQ. Easy peasy, right? It's like drawing a line on a piece of paper, but with way more mathematical significance. These segments are the building blocks for all sorts of shapes. Triangles? Yep, made of line segments. Squares? You guessed it!

But here’s where it gets a little more interesting: distance. How far apart are these two points? How long is that road we just built between P and Q? This is where the Common Core really wants you to get your hands dirty. Distance is all about measurement. We want to put a number on that relationship between points.

If your points are chilling on a number line, like on a super-duper skinny road, finding the distance is a breeze. Let’s say you have point A at 3 and point B at 7. How far apart are they? You just subtract the smaller number from the bigger one, right? 7 - 3 = 4. The distance between A and B is 4 units. Simple! What if point C is at -2 and point D is at 5? Again, the bigger minus the smaller: 5 - (-2) = 5 + 2 = 7. The distance is 7 units. You can’t have a negative distance, because distance is always a positive thing. It’s like telling someone how long your commute is – you wouldn't say it's "-15 minutes," you'd say it's "15 minutes," even if you're feeling particularly zippy that day.

But what happens when your points aren't just chilling on a single line? What if they’re in a full-blown 2D world, like on a graph? This is where things get a little more… graphical. You've probably seen those coordinate planes in your math class, right? The ones with the x-axis and the y-axis, looking like a giant plus sign on a grid. Our points will have coordinates here, like (x1, y1) and (x2, y2). It’s like giving each point an address in a city.

Now, to find the distance between two points on a graph, we need a little bit of magic. Don’t worry, no rabbits or top hats involved. We’re going to use the Distance Formula. This formula is your best friend for this kind of problem. It’s derived from something called the Pythagorean Theorem, which you might have heard of. Think of it as a right-angled triangle helper. If you draw a line segment between your two points, you can imagine a right triangle where that line segment is the hypotenuse (the longest side, opposite the right angle).

The distance formula looks like this (try not to faint):

Distance = √[(x2 - x1)² + (y2 - y1)²]

Whoa, okay, take a deep breath. Let’s break it down. * √ : That's the square root symbol. It’s like saying, "What number, when multiplied by itself, gives you the number inside?" * (x2 - x1)² : This part finds the horizontal distance between your two points. You take the x-coordinate of the second point and subtract the x-coordinate of the first point. Then, you square that difference (multiply it by itself). This ensures the distance is always positive, whether x2 is bigger or smaller than x1. It’s like making sure your step count is always a positive number, no matter which direction you take your steps.

* (y2 - y1)² : This part does the same for the vertical distance. You take the y-coordinate of the second point, subtract the y-coordinate of the first point, and then square that difference. Again, always positive!

* + : We add those two squared differences together. This is where the Pythagorean Theorem comes in! It’s literally a² + b² = c², where 'a' and 'b' are the lengths of the two shorter sides of our imaginary right triangle, and 'c' is the hypotenuse (our distance!).

* √[...] : Finally, we take the square root of the whole sum. This gives us the actual length of the line segment – the distance between our two points.

Let’s try an example, because examples are like a cheat sheet for your brain! Suppose you have point A at (2, 3) and point B at (5, 7).

1. First, find the difference in x-coordinates: x2 - x1 = 5 - 2 = 3.
2. Then, square that difference: 3² = 9.
3. Next, find the difference in y-coordinates: y2 - y1 = 7 - 3 = 4.
4. Square that difference: 4² = 16.
5. Add the squared differences: 9 + 16 = 25.
6. Finally, take the square root of the sum: √25 = 5.

So, the distance between point A and point B is 5 units! How cool is that? You just calculated the length of a line segment in a 2D space without even picking up a ruler. It's like having a superpower!

What if one of your coordinates is negative? Let’s say point C is at (-1, 2) and point D is at (3, -4).

1. Difference in x: x2 - x1 = 3 - (-1) = 3 + 1 = 4.
2. Square it: 4² = 16.
3. Difference in y: y2 - y1 = -4 - 2 = -6.
4. Square it: (-6)² = 36. (Remember, a negative number squared becomes positive! This is why squaring is so handy.)
5. Add them: 16 + 36 = 52.
6. Take the square root: √52.

Now, √52 might not be a nice, clean whole number. And that’s okay! Sometimes, the distance is a decimal or an irrational number. Your homework might ask you to leave it as a simplified radical (like √52 can be simplified to 2√13) or to round it to a certain decimal place. Just follow the instructions! It’s like a treasure hunt where the treasure might be a slightly messy pile of gold coins.

So, what are line segments again? They're the straight paths connecting two specific points. They have a definite length, and that length is what we're calculating with the distance formula. Think of them as the "sides" of shapes when you’re drawing. When you’re working on your homework, and you see a picture with points and lines, you’re likely identifying these line segments. You might be asked to find the length of a specific segment, or maybe the perimeter of a shape (which is just the total length of all its line segments added together!).

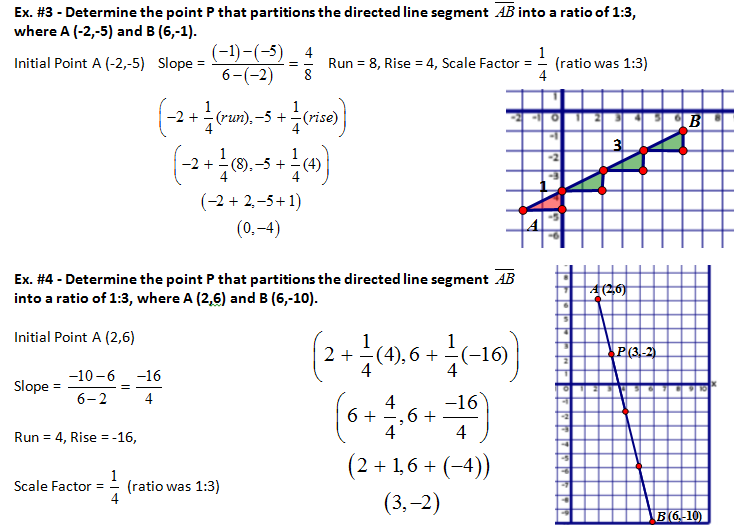
Sometimes, your homework might involve finding the midpoint of a line segment. This is like finding the exact halfway point of that road between two cities. The midpoint formula is another handy tool. If your points are (x1, y1) and (x2, y2), the midpoint (xm, ym) is calculated as:

xm = (x1 + x2) / 2

ym = (y1 + y2) / 2

See? You just average the x-coordinates and average the y-coordinates. It’s like finding the average of your test scores to see where you stand. Easy, right? This isn’t directly about distance, but it's closely related to line segments and helps you understand their structure.

Why is all this important, you might ask? Well, besides passing your geometry class (which is a pretty big deal!), understanding points, distance, and line segments is the foundation for so much more in math and science. It helps us understand maps, build structures, create computer graphics, and even navigate through space! You’re not just doing homework; you’re learning to describe and measure the world around you in a precise and powerful way. It’s like learning a new language – the language of space and shape.

So, don't let those formulas scare you. Think of them as tools in a toolbox. You wouldn't be afraid of a hammer, right? You'd just use it to build something cool. These formulas are the same! They help you build understanding.

When you’re tackling those problems, remember to:

• Identify your points: Make sure you know which (x, y) pair belongs to which point.
• Plug them into the formula carefully: Double-check your subtractions and especially your squarings. A tiny sign error can send your answer on a wild goose chase!
• Simplify if asked: If you get a radical, see if you can break it down.
• Visualize: Sometimes, sketching a quick graph can help you see what’s going on and even estimate your answer, which is great for checking your work.

And most importantly, be patient with yourself! Math is like a muscle. The more you work it out, the stronger it gets. Each problem you solve, each formula you use, makes you a little bit smarter, a little bit more capable. You’ve got this! You’re not just completing homework; you’re building a solid foundation for future discoveries, and that’s something to feel really, really good about. Go forth and conquer those points, distances, and line segments with a smile – you’re doing great!