Perform The Following Computation With Radicals Simplify The Answer
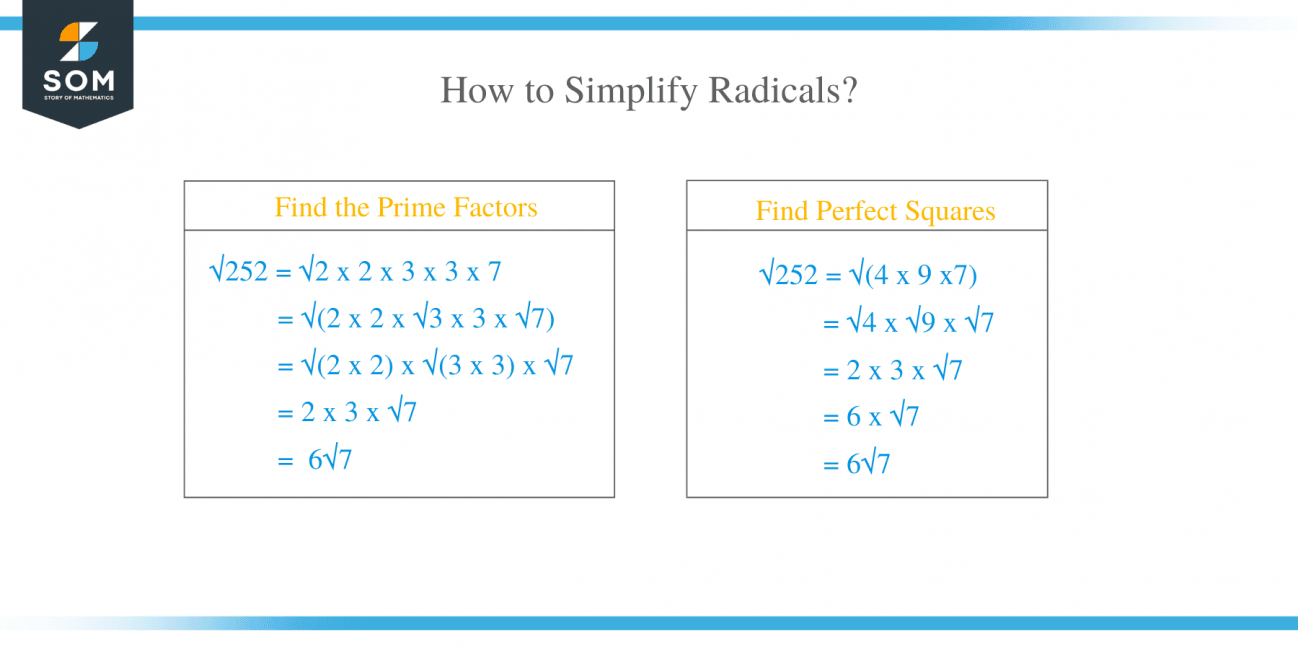
Hey there, fellow adventurers in the land of numbers! Ever stumbled upon a math problem that looks a little like a tangled vine, all twisty and knotted? You know, the kind with those funky symbols called radicals? Well, today we're going to untangle one of those together, and trust me, it’s more of a friendly puzzle than a brain-buster. We’re going to perform a computation with radicals and then, the really satisfying part, simplify the answer. Think of it like finding a hidden treasure chest after a bit of a hike.
So, what exactly is a radical? If you've ever seen that little checkmark-looking symbol (√), that's a radical! It’s basically asking a question: "What number, when multiplied by itself a certain number of times, gives us the number inside?" For example, the square root of 9 (√9) is 3, because 3 x 3 = 9. Easy peasy, right? It’s like asking, "What’s the side length of a square if its area is 9 units?"
But sometimes, numbers don’t play so nicely. What about the square root of 8 (√8)? 8 isn't a perfect square like 9 or 16. So, what do we do? This is where the fun begins! We can actually break down that number inside the radical into its smaller pieces, its factors. Think of it like finding prime numbers, the building blocks of all numbers. For √8, we can see it's 4 x 2. And hey, 4 is a perfect square! That's our clue.
Now, here’s the cool trick: if we can pull out a perfect square from inside the radical, we can take its square root and put it outside. So, √8 becomes √(4 x 2). Since we know √4 is 2, we can rewrite it as 2√2. See? We’ve simplified it! It’s like taking a big, unwieldy piece of luggage and breaking it down into smaller, more manageable bags. The 2 is now out front, and the √2 is still there, but it's a much simpler form of √8.
This process of breaking down and simplifying is super important when we start doing computations with radicals. Imagine you have to add √8 and another radical, say √2. Without simplifying first, it's like trying to add apples and oranges. You can't just say you have "√8 apples" and "√2 apples" and combine them easily. But if we remember our trick, √8 is the same as 2√2. So, the problem becomes adding 2√2 and √2.
Now, think of √2 as a single unit, like saying "two apples." So, if you have "two apples" (2√2) and you add "one apple" (√2), you end up with "three apples" (3√2). It's that simple! When radicals have the same number inside after simplification, we can just add or subtract the numbers in front of them. It’s like gathering your like terms in algebra, but with a cool radical twist.

Let's try a slightly more complex computation, shall we? Imagine we need to compute something like this: (√12 + √27) - √75. Whoa, right? Looks a bit intimidating. But remember our strategy: simplify each radical first.
Let's tackle √12. What are its factors? We know 12 is 4 x 3. And 4 is a perfect square! So, √12 becomes √(4 x 3), which simplifies to 2√3. Nice!
Next up, √27. What are its factors? 27 is 9 x 3. And 9 is a perfect square! So, √27 becomes √(9 x 3), which simplifies to 3√3. Look at that, another √3! We're starting to see a pattern here, aren't we?

Finally, √75. Let's find its factors. 75 is 25 x 3. And 25 is a perfect square! So, √75 becomes √(25 x 3), which simplifies to 5√3. Wow, everything broke down to have a √3 inside! This is like hitting the jackpot in a math game.
Now, let's plug our simplified radicals back into our original computation: (2√3 + 3√3) - 5√3.
Inside the parentheses, we have 2√3 + 3√3. Since both have √3, we add the numbers in front: 2 + 3 = 5. So, that part becomes 5√3.

Now our computation looks like: 5√3 - 5√3.
And what happens when you subtract something from itself? You get zero! So, 5√3 - 5√3 = 0.
Isn’t that neat? We started with a seemingly complicated expression with radicals, and after a bit of simplification and computation, we ended up with a nice, clean zero. It's like a magic trick, but with math!

Why is this so cool? Because it shows us that even complex-looking math problems can be broken down into simpler steps. It teaches us the power of finding common factors and simplifying. Think of it like being a detective: you gather clues (simplify radicals), you analyze them, and then you solve the case (perform the computation).
This skill of simplifying radicals isn't just for show. It's fundamental in higher math, like algebra and calculus. It helps us keep equations tidy and makes complex calculations much more manageable. Imagine trying to build a skyscraper without having proper tools to measure and cut materials – it would be a mess! Simplifying radicals is like having the right tools in our mathematical toolbox.
So, next time you see a problem with radicals, don't get discouraged. Take a deep breath, remember your simplification tricks, and approach it with a curious mind. You might be surprised at how elegant and satisfying the solution can be. It's a little bit of detective work, a dash of puzzle-solving, and a whole lot of number crunching fun. Happy simplifying, everyone!
