Pascal Triangle In Python Without Using Function

Ever stumbled upon a neat mathematical pattern and thought, "Wow, that's kind of cool!"? Well, the Pascal Triangle is exactly that kind of pattern, and it's surprisingly easy to bring to life using Python, even without diving into the complexities of functions. It’s a fantastic way to dip your toes into both number theory and basic programming in a way that feels more like a playful exploration than a chore.
So, what exactly is this Pascal Triangle all about? Imagine an infinitely growing pyramid of numbers. It starts with a single '1' at the very top. Each subsequent row is built by adding together the two numbers directly above it. If a number is at the edge, it's considered to have a '0' above it, so it just inherits the number from the single number above it. This simple, almost recursive, construction leads to some incredibly beautiful and useful properties.
The benefits of understanding Pascal's Triangle are more far-reaching than you might initially think. For starters, it's a gateway to understanding binomial coefficients, which are crucial in probability and statistics. They help us figure out how many ways we can choose a certain number of items from a larger set. Think about the odds of winning a lottery or the probability of getting a certain combination of heads and tails when flipping coins – Pascal's Triangle is lurking in the background, providing the answers.
Beyond the academic, you can see its influence in areas like computer science, particularly in algorithms related to combinations. In education, it’s a brilliant tool for teaching about mathematical sequences, patterns, and the fundamental operations of addition. Even in everyday scenarios, understanding combinations can help with tasks like planning seating arrangements or selecting ingredients for a recipe where order doesn't matter.
Now, let's talk about making this happen in Python without using functions. This might sound a bit daunting, but it boils down to using loops and list manipulations. You can create a list representing the current row, and then, using another loop, generate the next row by summing adjacent elements from the previous one. It’s a very direct and visual way to build the triangle, line by line, directly in your code.
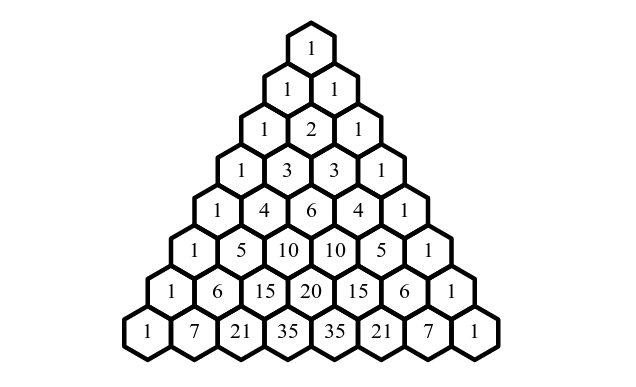
For instance, you could start with a list `[1]`. To get the next row, you’d create a new list, starting with `1`, then adding the elements of the previous list (just `1` in this case), and ending with another `1`. For the row after that, you’d take your `[1, 1]` row. The new row starts with `1`. Then you add the first and second elements of the previous row (`1 + 1 = 2`). Finally, the row ends with `1`. So you get `[1, 2, 1]`. You can keep this up, printing each row as you generate it.
A practical tip for exploration? Start small! Try to generate just 5 or 6 rows. Observe the patterns: the sum of numbers in each row, the appearance of powers of two, and the symmetry. You can then incrementally increase the number of rows and see how your Python code handles it. It's all about that iterative process of building and observing, making it a truly engaging way to learn.
