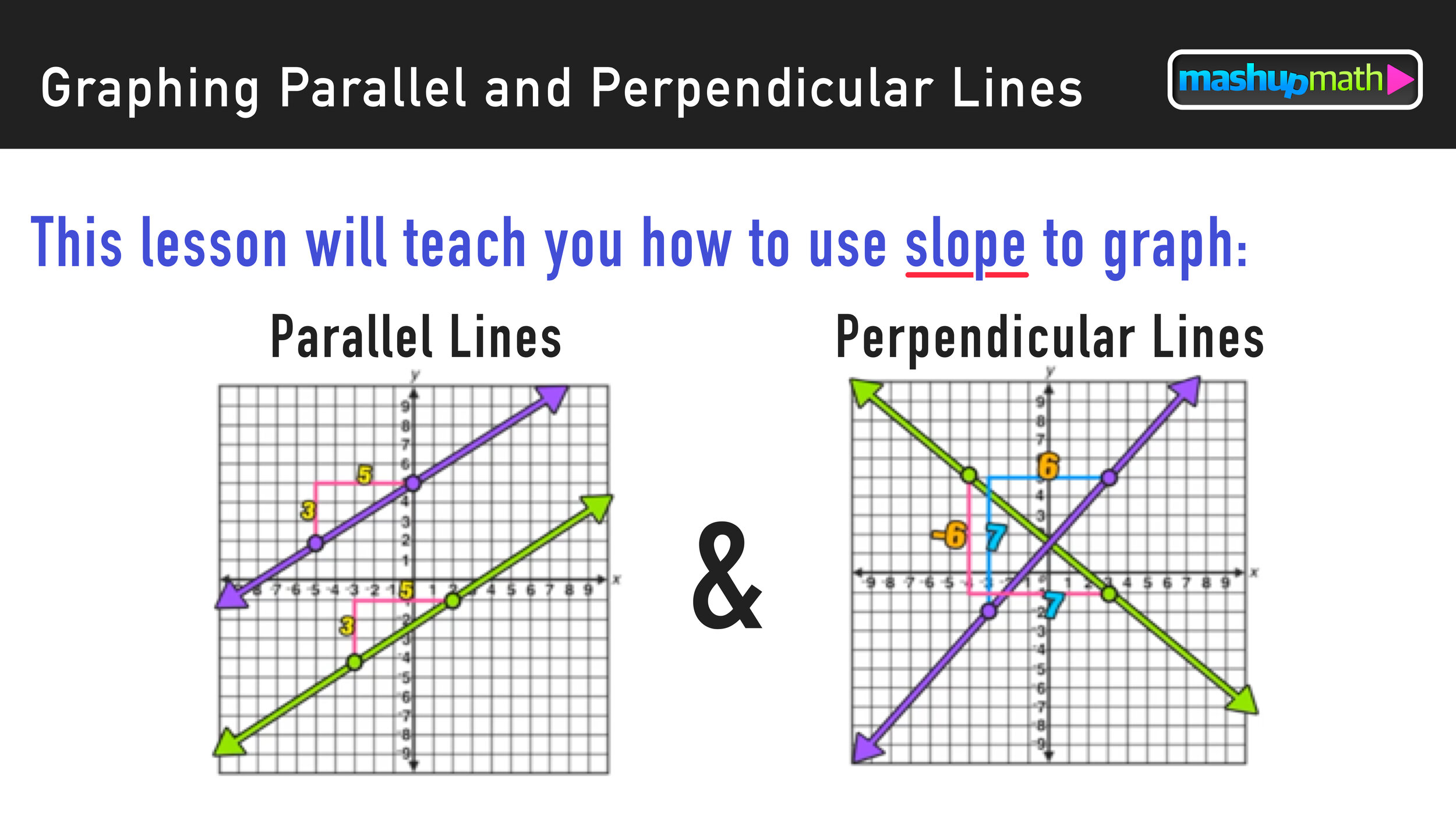
Parallel Lines Have The Same Slope True Or False
So, let's dive into something that might sound a little bit like a math puzzle, but honestly, it's more like a little secret that makes the world of lines make so much more sense. We're talking about a statement: "Parallel lines have the same slope." Sounds pretty official, right?
But here's the fun part: is that statement a true statement, or is it a big ol' false one? Imagine you're just chilling, sketching out some lines on a piece of paper. You draw one line, then you draw another one that looks exactly like it, just… shifted.
These lines, they never, ever cross. They're like best friends who always walk side-by-side. Think of train tracks. They run forever in the same direction and never bump into each other. That's the visual we're going for.
Now, the "slope" thing. What is slope? Think of it as how steep a line is. Is it climbing a mountain or just gently rolling down a hill? A steep line has a big slope. A flat line has a slope of zero. A line going downwards has a negative slope.
So, if two lines are perfectly parallel – meaning they'll never meet, no matter how far you extend them – it just makes sense that they'd have the same amount of "steepness," doesn't it? It's like they're on the same journey, at the same pace.
Think about it this way: if one line was super steep (a big slope) and its "parallel" buddy was barely slanting at all (a tiny slope), eventually, the steeper one would have to catch up and cross the other one. But parallel lines never cross. That's their whole deal.
This is where the magic happens! The statement "Parallel lines have the same slope" is not just some arbitrary rule. It's a fundamental characteristic that defines what it means for lines to be parallel. It’s like a fingerprint for parallel lines.
So, let's get to the big reveal. Drumroll please… TRUE! Yes, it is absolutely, unequivocally, TRUE. Parallel lines do have the same slope. It’s one of those beautiful, elegant truths in mathematics that just clicks.
Why is this so entertaining? Because it's a peek behind the curtain of how things work in a structured way. It's like solving a tiny, delightful riddle. You have this visual of lines never meeting, and then you have this concept of "slope," and they fit together perfectly.
It’s like finding out that all dogs wag their tails when they're happy. It’s a predictable, understandable behavior. Similarly, parallel lines having the same slope is a predictable, understandable geometric truth.
What makes it special? It’s the simplicity of it. There’s no complex jargon, no convoluted formulas needed to grasp this core idea. You can imagine it, you can draw it, and then you can understand why it’s true. It’s accessible.
Imagine you're a detective. You're looking for clues. The "same slope" is the ultimate clue that tells you, "Aha! These lines are definitely parallel." You don't need any other evidence. It's a foolproof identifier.
This isn't about memorizing facts for a test. It's about understanding a fundamental concept that pops up everywhere. From designing buildings to mapping out roads, the idea of parallel lines and their slopes is quietly working behind the scenes.
Think about how satisfying it is when things just fit. Like a puzzle piece slotting perfectly into place. That's the feeling you get when you understand this statement. The visual of parallel lines and the abstract concept of slope align harmoniously.
It’s a little bit of math that feels like a little bit of magic. You can picture the lines, you can think about their steepness, and then you realize they have to be the same for the lines to stay apart forever. It’s a visual and conceptual dance.
This little nugget of information is like a key that unlocks more understanding. Once you get this, other geometric ideas start to make more sense. It's a building block, but a really fun and easy one to build with.
And the best part? You don't need to be a math whiz to appreciate it. You just need a little bit of curiosity and maybe a pencil and paper to sketch it out. Seeing is believing, and in this case, seeing helps you understand.
So, next time you see two lines that look like they're going in the same direction and will never meet, you can confidently say, "Yep, they've got the same slope!" It's like knowing a secret handshake for geometry.
This truth is so elegant because it’s so direct. It doesn't try to be complicated. It just is. The universe of lines has this beautiful, ordered rule, and it’s not hidden in a dusty textbook; it's right there in front of you, waiting to be noticed.
It makes you wonder what other simple, elegant truths are out there, just waiting for us to spot them. This statement about parallel lines and slopes is an invitation to look closer at the world around you, because math is often a part of it.
It's a reminder that even in seemingly abstract concepts, there's often a practical, visual, and satisfying explanation. It's not just about numbers; it's about how things relate and behave. And the relationship between parallel lines and their slopes is a prime example.
So, yes, the statement "Parallel lines have the same slope" is absolutely TRUE. And hopefully, understanding why is as enjoyable for you as it is for us to share! It's a little piece of mathematical sunshine.
It’s the kind of thing that makes you nod your head and think, "Ah, that makes perfect sense!" It’s not a chore; it’s a moment of clarity. A small, but significant, understanding.
And that's the beauty of it, isn't it? Taking something that sounds a bit technical and making it feel intuitive and even a little bit fun. It's math for everyone, just presented in a way that sparks interest.
So, go ahead, embrace this little truth! It's a great starting point for exploring more of the fascinating world of geometry. You never know what other elegant secrets you might uncover.

The world of lines is full of these charming relationships. And the connection between parallel lines and their shared slope is a particularly delightful one. It’s a testament to the order and beauty that can be found in mathematics.
Think of it as a secret handshake you now know. You can spot parallel lines with confidence. And that’s a pretty cool superpower, right? Math can be like that.
So, the next time you're looking at graphs or diagrams, keep an eye out for those parallel friends. Remember their shared slope, and appreciate the simple, yet profound, truth they represent.
It's a concept that's both simple to understand and incredibly powerful in its implications. The statement is TRUE, and the reason behind it is elegantly straightforward.
And that, my friends, is why this little statement is so entertaining and special. It's a small window into a world of elegant mathematical truths that are always there, waiting to be appreciated.
So, yes, parallel lines have the same slope. It's a true statement, and a delightful one at that.
