Multiply Two And Five-eighths Negative Two And Three-fifths

Sometimes, math can feel like a grumpy old wizard, muttering secrets only he understands. But what if math could be a cheerful baker, whipping up delightful treats? Today, we're going to follow a little adventure with two numbers that might seem a bit unusual at first glance. Think of them as quirky characters in a playful story.
Our first character is Two and Five-eighths. Imagine a baker who's just measured out two whole, perfectly round cookies, and then added a little extra flourish of five-eighths of another cookie. It’s not a whole number, not quite a fraction of nothing, but somewhere delightfully in-between. This baker is feeling generous today!
And our second character? He's Negative Two and Three-fifths. This one's a bit more mysterious. Imagine a grumpy gnome who owes three-fifths of a shiny pebble to his neighbor. He's not quite at owing two whole pebbles, but he's definitely in the red. He’s got a bit of a frown, this one.
Now, these two characters are going to meet, not for a chat over tea, but for something much more energetic: a multiplication dance! This isn't just any dance; it’s a special kind of tango where their values swirl and twirl together. It’s a bit like mixing two different flavored candies to see what new taste emerges.
First, let's help our characters get ready for the dance. They need to be dressed in their "improper fraction" outfits. This just means they need to put on their dancing shoes that make them look a little different. Two and Five-eighths becomes Twenty-one eighths. Think of it as taking all those cookie bits and lining them up neatly.
And Negative Two and Three-fifths? He transforms into Negative Thirteen fifths. That grumpy gnome has now counted up all his tiny debts and presents them as one big, slightly less grumpy, "I owe you thirteen little fifths."
So, our dressed-up dancers are Twenty-one eighths and Negative Thirteen fifths. They’re ready to show off their moves! They’re not going to add or subtract; they’re going to multiply. This means they’re going to combine their efforts in a very specific, energetic way.

When two numbers multiply, their tops (numerators) do a little jig together, and their bottoms (denominators) do a similar jig. So, the twenty-one on top of our first dancer will twirl with the negative thirteen on top of our second. And the eight on the bottom will waltz with the five on the bottom.
The dance of the tops is quite lively: twenty-one times negative thirteen. This is where things get interesting. Imagine twenty-one cheerful fireflies suddenly deciding to borrow thirteen twinkles from a grumpy moon. The result will be a bit of a dimming, a definite decrease.
And the dance of the bottoms: eight times five. This is a simpler, more straightforward rhythm. Like eight little ants marching in a line, and then five such lines appear. It's a steady, predictable beat.
So, the tops combine to give us negative two hundred seventy-three. That grumpy gnome's debts have really piled up when you combine them with the baker's extra cookie bits in this way! It's a significant amount of owed shinies. It’s the mathematical equivalent of a mild case of the Mondays.
And the bottoms combine to give us forty. Those marching ants have formed a neat little square. It’s a solid, foundational number.
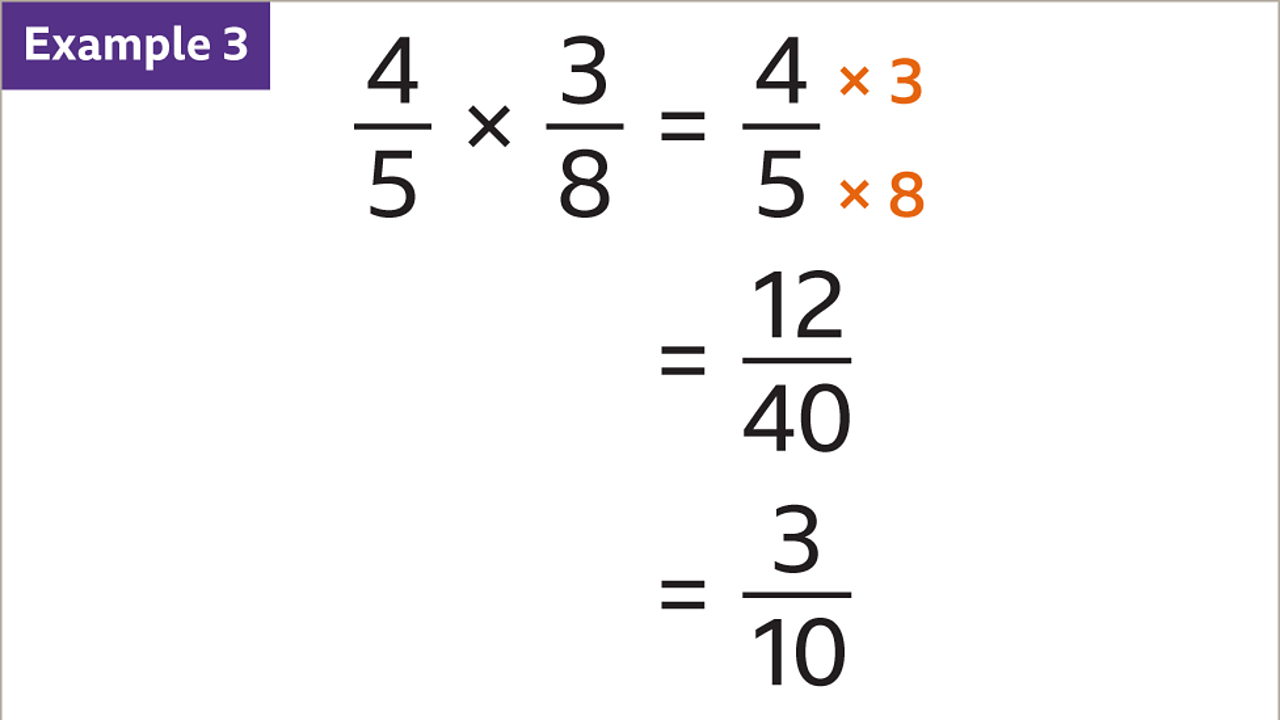
Now, our dancers have finished their grand multiplication tango. They've produced a brand new number: Negative Two Hundred Seventy-Three Fourtieths. It's a fraction, and a negative one at that! It’s like finding out that grumpy gnome’s debts have somehow gotten even bigger, and it's all thanks to his dance with the generous baker.
But the story doesn’t end there! Math loves to tidy up, and this fraction, Negative Two Hundred Seventy-Three Fourtieths, can be tidied up too. We can see how many whole "fortieths" are hiding inside it. It’s like asking, "How many times does a tiny coin fit into a much larger, slightly leaky bucket?"
When we divide two hundred seventy-three by forty, we find that it fits in six whole times. Think of it as six full buckets of debts. And there’s a little bit left over.
The remainder is thirty-three. So, we have six whole buckets of debt, and then an additional thirty-three fortieths of a bucket still owed. This means our grumpy gnome is now owing Six and Thirty-Three Fortieths.
And because the original multiplication involved a negative number, our final answer is also negative. So, the grand finale of our multiplication dance is Negative Six and Thirty-Three Fortieths. It’s a surprisingly neat conclusion to our numerical adventure.
What's heartwarming here? Well, even with a negative outcome, there's a kind of order to it. The grumpy gnome and the generous baker, through their energetic dance, have arrived at a clear, understandable result. Math, in its own way, always brings things to a resolution.
And humorous? Imagine the gnome’s surprise! He thought he was just dealing with a few small debts, and then the baker’s extra cookies somehow made everything… worse, in a mathematically precise way. It's a gentle reminder that sometimes, the most unexpected combinations lead to the most significant, albeit sometimes slightly negative, outcomes.
So, next time you see numbers like Two and Five-eighths or Negative Two and Three-fifths, don't be intimidated. Think of them as characters in a story, ready for their next mathematical dance. They might just surprise you with the delightful (or in this case, slightly daunting) results they can create together.
It’s all about seeing the playful side, the gentle rhythm, and the surprising conclusions that numbers can offer. Math isn't just about hard rules; it's about stories, transformations, and sometimes, a good old-fashioned multiplication tango that ends with a clear, if slightly indebted, answer.

Even when a negative result appears, it's a sign of a well-executed calculation. It’s the universe of numbers saying, "Here’s what happens when these two forces meet." And understanding that meeting, that interaction, is the real magic.
So, the next time you're faced with multiplying mixed numbers, especially negative ones, remember our baker and our gnome. Imagine their dance, their transformation, and the final, neatly packaged result. It’s a little bit of math magic, served with a side of fun.
And that’s how Two and Five-eighths multiplied by Negative Two and Three-fifths leads us to Negative Six and Thirty-Three Fortieths. A journey from individual characters to a combined, conclusive story. A story of numbers, dancing and resolving.
It’s a testament to the fact that even when dealing with seemingly complex situations, a step-by-step approach, with a touch of imagination, can make the process enjoyable and the outcome clear.
So, embrace the numbers, let them dance, and enjoy the fascinating, sometimes surprising, world they create.
