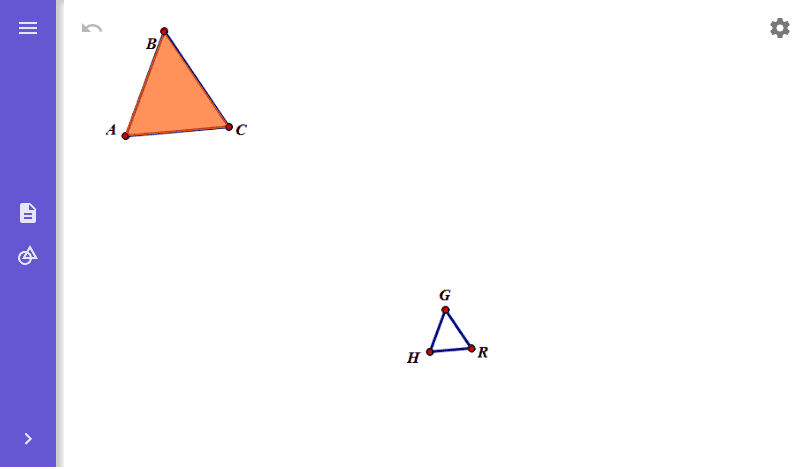Multiple Similarity Transformations Are Performed On A Triangle

Imagine you have a perfectly lovely triangle. It’s like a little LEGO brick of geometry, simple and neat. Now, what if we decided to have a little fun with it? We’re not just going to look at it; we’re going to play dress-up with it, but in a super-duper mathematical way!
Think of it like this: you’ve got your favorite t-shirt. First, you might stretch it out a bit, making it bigger but keeping its shape. Then, maybe you decide to flip it upside down, like a playful somersault. And perhaps, you even decide to slide it across the room, just for a change of scenery. We’re doing all of that, but with our little triangle friend!
The magic here is that we can perform these amazing feats on our triangle, one after another, and still have a perfectly recognizable, albeit transformed, version of our original. It’s like giving your t-shirt a whole makeover, but it's still, fundamentally, your t-shirt.
The Grand Transformations!
Let’s meet our main players in this geometric party. First up, we have the “Stretch and Squish”, officially known as a dilation. This is where our triangle can become a tiny speck or a gigantic, wall-filling behemoth. It’s all about changing its size, making it a mini-me or a super-sized version.
Then, we’ve got the ever-so-dramatic “Flip and Flop”, also called a reflection. Imagine looking at your triangle in a mirror. The image you see is its reflection. It's like a perfectly flipped twin, but backward!
Next, let’s talk about the graceful “Spin Cycle”, also known as a rotation. This is where our triangle twirls and whirls around a central point. It can do a little pirouette or a full 360-degree ballet performance.
And finally, we have the smooth operator, the “Slide and Glide”, or translation. This is the simplest move of all – just picking up the triangle and moving it somewhere else without changing its size or orientation. It’s like pushing it across a table.
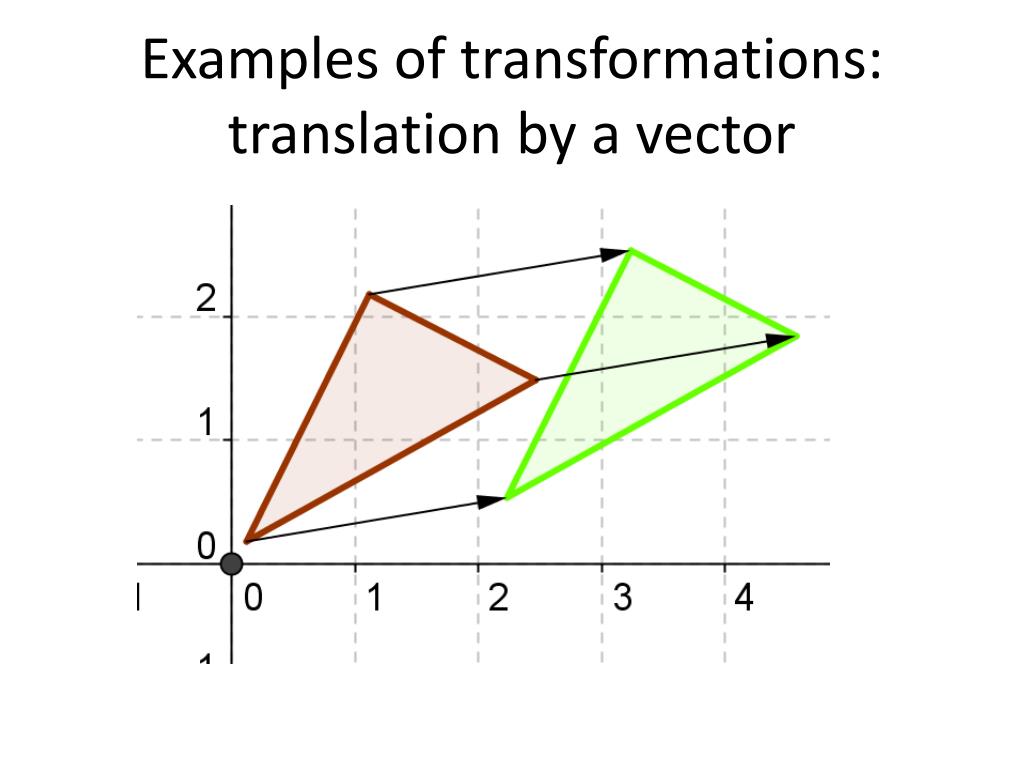
Layering the Fun!
Now, here’s where the real excitement kicks in. We don’t just do one of these transformations. Oh no! We can do them in any order, any combination, and as many times as our hearts desire. It’s like building a magnificent sandwich with all your favorite ingredients layered just so.
Imagine you take your little triangle, let’s call him “Timmy”. First, you might decide to stretch Timmy to be twice as big. That’s a dilation! Then, you might flip him upside down. That’s a reflection!
And then, just for giggles, you might decide to slide the flipped, stretched Timmy over to the other side of the page. That’s a translation!
Each of these steps, these similarity transformations, preserves the shape of Timmy. He might be bigger, smaller, upside down, or in a completely new spot, but he’s still undeniably Timmy, just in a different outfit and pose. The angles stay the same, and the ratios of the sides remain consistent.

It’s Not Just About Triangles!
This isn’t just some weird mathematical party for triangles. This concept applies to any shape! Imagine doing this with a square, a star, or even a smiley face. You can stretch it, flip it, spin it, and slide it, and it will always maintain its fundamental essence.
Think about how cartoon characters are animated. They might be resized, rotated, and moved around the screen. These are all practical, everyday examples of similarity transformations happening right before your eyes!
Even in video games, when you see characters appear, disappear, grow, or shrink, those are all forms of these transformations at play. It’s the secret sauce that makes digital worlds dynamic and exciting.
Why is this So Cool?
Well, for starters, it’s incredibly powerful! Being able to manipulate shapes in predictable ways opens up a universe of possibilities. It's how we design buildings, create art, and even understand the universe around us.
It’s also wonderfully intuitive. We naturally understand the idea of making something bigger or smaller, flipping it, or moving it. These mathematical transformations just give us the precise language and tools to describe and control these actions.
The beauty of performing multiple similarity transformations is that the end result is always another shape that is similar to the original. This means all the angles are preserved, and the lengths of the sides are scaled proportionally. It’s like having a perfect blueprint that you can enlarge or shrink, flip or rotate, and it still perfectly represents the original design.
So, the next time you see a triangle, or any shape for that matter, give it a little wink. It might just be preparing for its next big transformation, a dazzling dance of size, orientation, and position, all while staying true to its geometric roots!
It’s like the ultimate makeover for shapes, where they can try on different looks and still be perfectly themselves. How fabulous is that?
Similarity Transformations – GeoGebra
And the best part? You can be the director of this geometric show! You decide the order, the magnitude, and the style of each transformation. You are the maestro of similarity!
Think of it as a geometric playground. You can take your little triangle and build an entire landscape of transformed versions, each one unique but connected to the original by the magic of similarity.
It's a reminder that even with changes, the core essence of something can remain. Our triangle might change its appearance drastically, but its fundamental geometric identity is unbreakable through these playful manipulations.
So, embrace the transformations! Let your triangles stretch, flip, spin, and slide. It’s a joyous celebration of shape, size, and space, all rolled into one delightful geometric adventure!