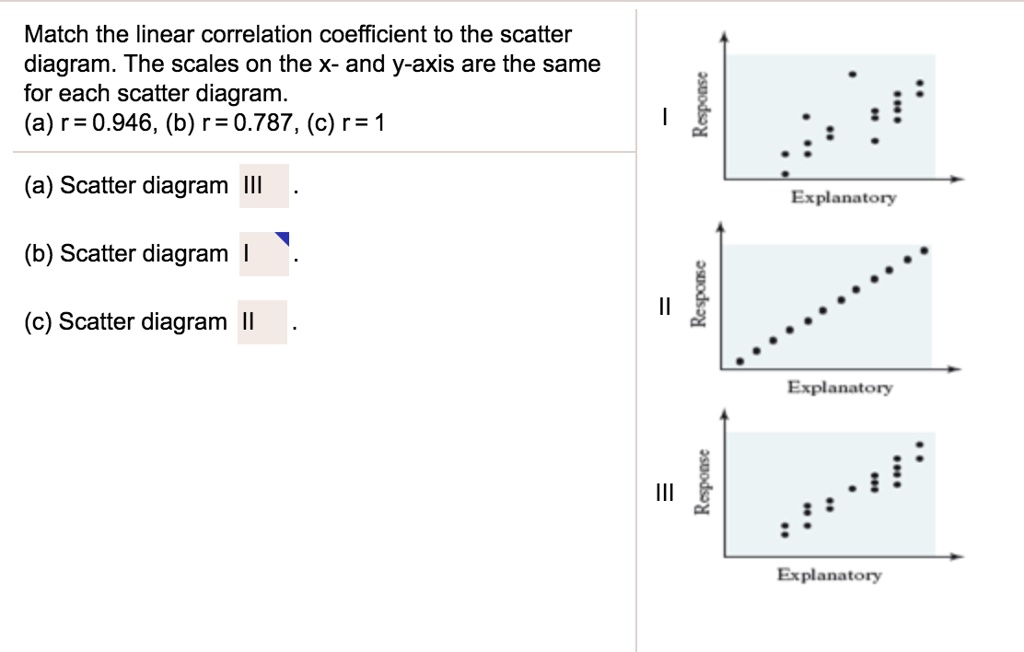
Match The Linear Correlation Coefficient To The Scatter Diagram
Imagine you’re at a bustling party, and you’re trying to figure out who’s who and what’s what. You see a bunch of people chatting, some in tight little groups, others milling about, and a few loners nursing their drinks. Now, imagine you’ve got a special superpower: you can instantly tell how connected all these partygoers are, not just in their conversations, but in a general, observable way. That’s kind of what matching the linear correlation coefficient to a scatter diagram is all about, but for data instead of people!
Think of a scatter diagram as a snapshot of a party for numbers. Each little dot on the graph represents a pair of numbers, like maybe how many hours someone studied for a test versus the grade they got. We’re not going to get bogged down in the nitty-gritty of calculating this correlation coefficient (that’s like the super-secret handshake of statistical connection). What matters is what it tells us, and it tells us a delightful story about how things relate to each other.
Let’s start with the rockstars of correlation, the ones who make you nod your head and say, "Yep, that makes sense!" These are the ones with a correlation coefficient close to +1. When you see a scatter diagram with dots marching steadily upwards from left to right, like a cheerful conga line of numbers, you know you’ve got a strong positive relationship. It’s like when the more ice cream you eat, the happier you get (mostly!). Or the more you practice your ukulele, the better you sound. It’s that warm, fuzzy feeling of things going up together. You might see this in something like temperature and the number of ice cream sales. As the temperature climbs, so do the ice cream sales, in a pretty predictable way. It’s the statistical equivalent of a high-five between two related trends.
Then we have the opposite end of the spectrum, the grumpy twins who go in opposite directions. These are the numbers close to -1. In their scatter diagram, the dots tumble downwards from left to right, like a sad avalanche of data. This is a strong negative relationship. Think about it: the more time you spend playing video games, the less time you have to do chores. Or, the more you procrastinate, the closer your deadline gets. It’s that feeling of "as one goes up, the other goes down." Imagine the relationship between the number of hours spent sleeping and the number of cups of coffee needed to stay awake. Generally, the more sleep you get, the less coffee you need. This is a classic negative correlation, and the scatter diagram will show a clear downward trend, like a sigh of relief that you don’t need that extra caffeine!
Now, things get a bit more… interesting. What about the scatter diagrams where the dots are scattered all over the place, like confetti after a parade? These are the ones with a correlation coefficient close to 0. This suggests there’s very little to no linear relationship between the two sets of numbers. It’s like trying to find a connection between the number of pigeons in the park and the price of tea in China. They’re just doing their own thing, independently. You might see this in the relationship between the color of your socks and your mood for the day. Unless you have a very specific sock-mood ritual, these two things are likely to be completely unrelated. The scatter diagram would look like a random splatter of paint, offering no clear direction or pattern.
But here’s where the fun really starts! Sometimes, you’ll see a pattern that’s not perfectly straight, but it’s still got a bit of a lean. Maybe the dots are clustered somewhat, but there’s a bit of a wiggle in the line. These are the ‘meh’ correlations, hovering somewhere between 0 and +1, or 0 and -1. They suggest a weak positive or negative relationship. It's like saying, "Yeah, they tend to go in the same direction, but not always, and not by much." Think about the relationship between the number of times you check your phone and the number of people you hug in a day. There might be a tiny, almost imperceptible tendency for them to be slightly linked, but it's hardly a guarantee. The scatter diagram would show a loose cloud of dots, with a vague upward or downward drift, but plenty of exceptions.
The beauty of matching these coefficients to diagrams is that it’s like solving little puzzles. You look at the dots, and your brain, with a little help from these numbers, starts telling you a story. Is it a story of things growing together, like friendship and shared laughter? Is it a story of things balancing each other out, like effort and reward? Or is it a story of complete randomness, like finding a four-leaf clover on the sidewalk? Each scatter diagram is a little tableau, and the correlation coefficient is its witty narrator, whispering the secrets of their connection. It’s a way to understand the world around us, not just with our eyes, but with a deeper sense of how things dance together, or stubbornly refuse to.
