Match Each Trigonometric Function With One Of The Graphs
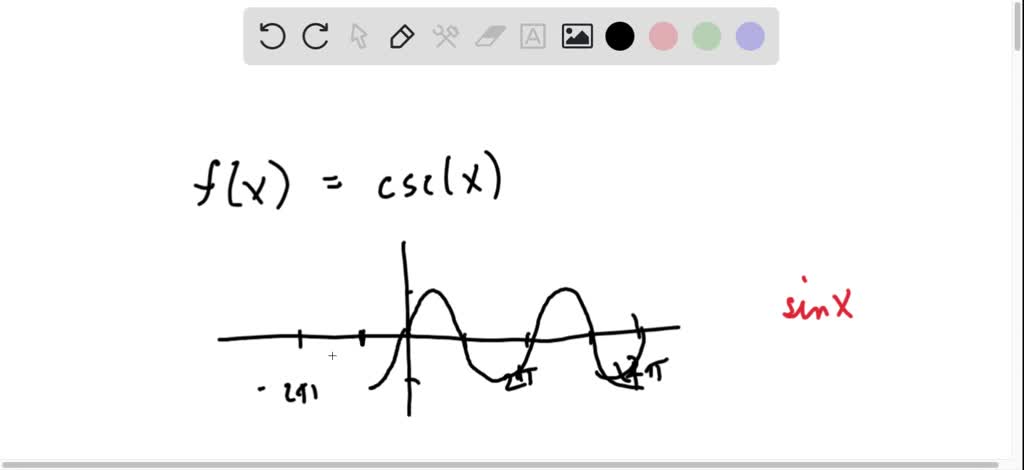
So, we're staring at a bunch of squiggly lines. They look like they were drawn by a caffeinated spider. And someone, somewhere, decided these were important. More important than, say, finding your car keys.
These, my friends, are the faces of our trigonometric functions. They're like the awkward cousins at a family reunion, each with their own distinct personality. Some are smooth and predictable. Others are… well, let's just say they have a flair for the dramatic.
The Usual Suspects
First up, we have our trusty sine wave. It's the one that looks like a perfectly modulated hum. Think of it as the reliable friend who always shows up on time. It starts at zero, goes up, then down, then back to zero. A true classic.
Then there's cosine. It's like sine's twin brother, but with a bit of a late start. Cosine waves are identical to sine waves, but they're shifted over a little. It's like cosine decided to grab an extra cup of coffee before joining the party. Still smooth, still predictable, just fashionably delayed.
And then we meet tangent. Oh, tangent. Tangent is the wild child. It doesn't just go up and down; it goes way up and way down, and then suddenly reappears from the other side. It has these vertical breaks, these little leaps of faith. Tangent is definitely the one who would try to crowd-surf at a concert.
The Less Common, But Still Fascinating
Now, let's talk about the others. These are like the supporting actors who deserve their own spotlight. First is cosecant. Cosecant is basically the inverse of sine. Imagine sine being the calm ocean, and cosecant is those moments when a rogue wave suddenly appears. It's the echo of the sine wave, but with a lot more oomph between the peaks and valleys.
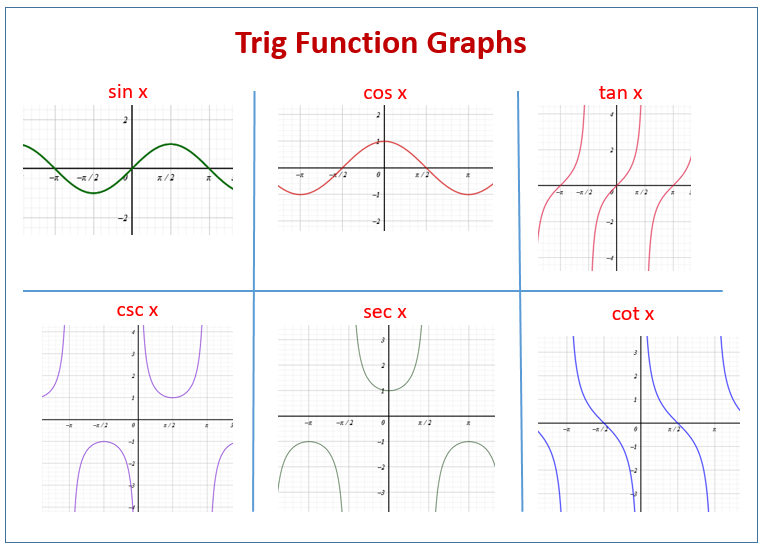
Next, we have secant. You guessed it, it's the inverse of cosine. If cosine is that smooth, rolling hill, secant is the view from the very top of that hill, with a sudden, dramatic drop on the other side. It mirrors cosine's dance but with an even grander, more exaggerated flair. It's like cosine took a roller coaster and secant is the thrill of the steepest drop.
Finally, there's cotangent. This one is the inverse of tangent. Remember tangent's dramatic leaps? Cotangent does something similar, but it's flipped. It's like taking that wild party animal and making them do a graceful ballet, but with occasional, unexpected somersaults. It's got those breaks, those ascents and descents, but in a different rhythm.
Matching the Personalities
So, how do we tell them apart? It's like playing a guessing game with your friends. You look at their faces, their mannerisms. Are they calm and collected? Are they a bit wild? Do they have a habit of showing up late?
Look at the graph that's just a smooth, flowing wave, starting at the middle and going up and down. That's our sine. It's the baseline. It's the original smooth operator.

Now, find the wave that looks exactly like the sine wave, but it's shifted a bit to the right. It starts at its highest point. That's cosine. It's sine's slightly delayed but equally charming sibling. They’re so similar, it's almost a joke.
Here's where it gets exciting. See the graph with those sharp, vertical lines, where the wave disappears and reappears? That's the show-off, the attention-seeker. That's tangent. It's the one who can't stay in one place for too long. It breaks free from the expected.
Now, look for the graphs that have those "U" shapes pointing upwards and downwards, separated by those invisible lines. These are the ones that don't touch the x-axis in the same way as sine and cosine.
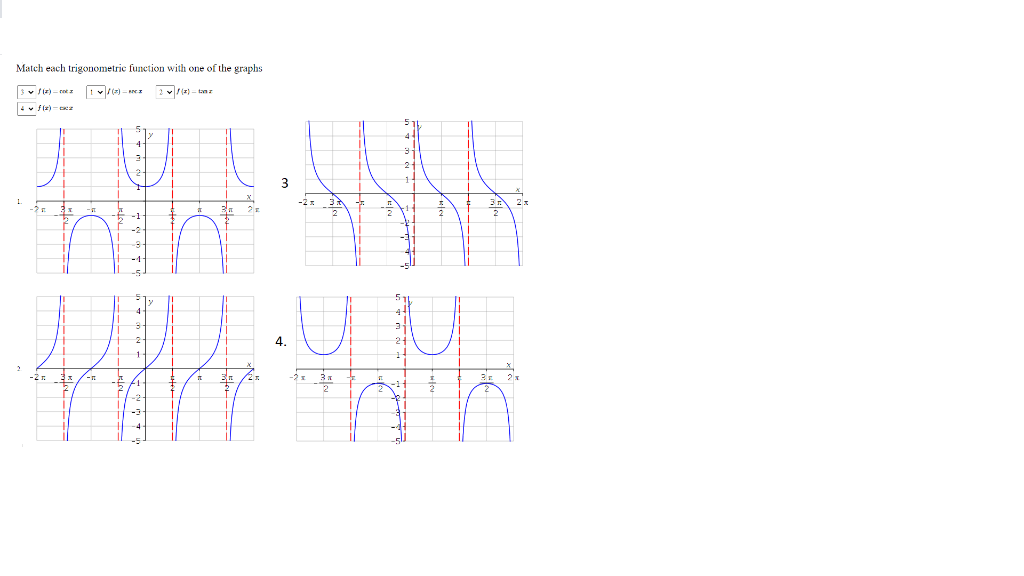
If you see those "U" shapes that are generally pointing upwards, and they seem to hug the lines where the sine wave would have been at its peaks and valleys, those are the cosecant graphs. They are the amplified versions of sine's journey, reaching for the heavens and diving deep into the abyss. They exist in the spaces between the sine waves.
Similarly, when you see those "U" shapes that are hugging the lines where the cosine wave would have been at its peaks and valleys, those are the secant graphs. They mirror cosine's path but with a more dramatic emphasis on the extremes. They're like the amplified echo of cosine's quiet steps.
And for cotangent? It's the inverse of tangent's craziness. Look for the graph that also has those vertical breaks, but it starts high and goes low, kind of like a mirrored and shifted tangent. It's got that zigzag energy but with a different starting point and direction. It's tangent's more thoughtful, yet still unpredictable, cousin.
The "Unpopular" Opinion
Honestly, sometimes I think these graphs are just the universe's way of having fun. They're like little mathematical doodles. And while some people might find them dry, I find them delightfully eccentric. They're not just numbers; they're little personalities dancing on a page.
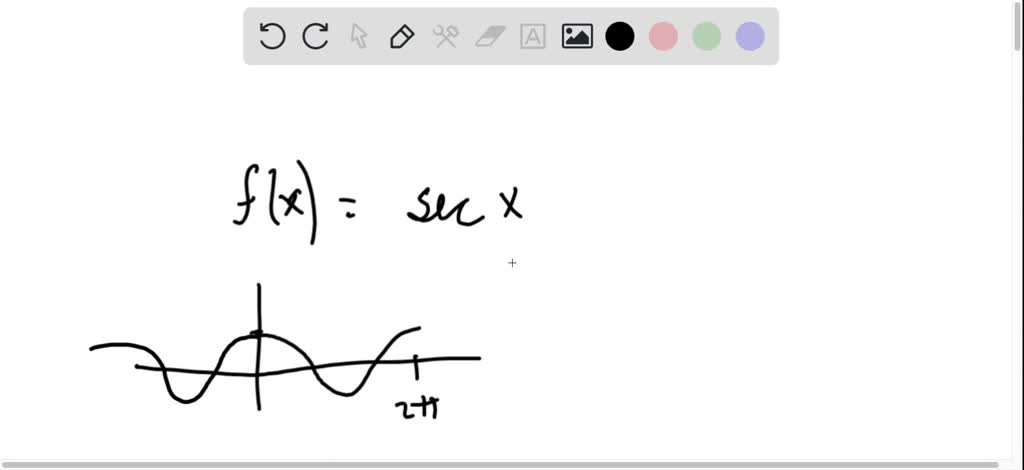
It's like trying to figure out which of your friends is which based on their silhouette. This one's got a certain swagger. That one's a bit more reserved. And then there's the one who's always doing something unexpected.
So, next time you see these graphs, don't just see lines. See the sine's gentle flow, the cosine's stylish arrival, the tangent's daredevil spirit. See the dramatic loops of cosecant and secant. And the quirky turns of cotangent. They're all just out there, doing their thing. And in their own way, they're pretty darn entertaining.
It’s a visual symphony, really. A bit chaotic, perhaps, but a symphony nonetheless. And matching them up is like playing a fun game of "guess who?" with the universe's most interesting characters.
My unpopular opinion? Trigonometric functions are basically the emojis of mathematics. Each one tells a story, just with more squiggles.
So go ahead, embrace the wiggle. Embrace the bounce. Embrace the breaks. These graphs are here to make math a little less intimidating and a lot more interesting. They're the proof that even abstract concepts can have personality. And sometimes, that personality is a little bit bonkers.
