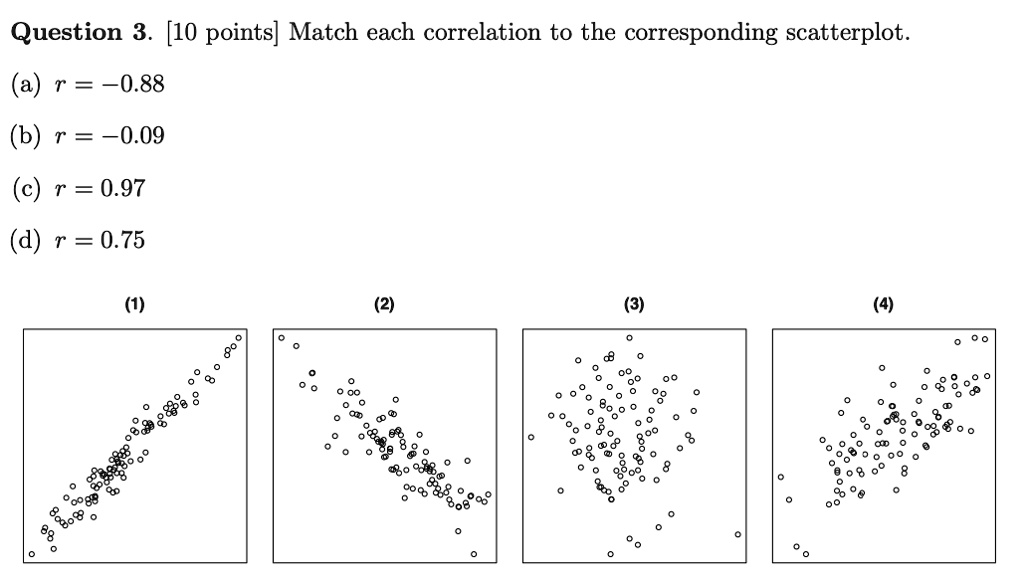
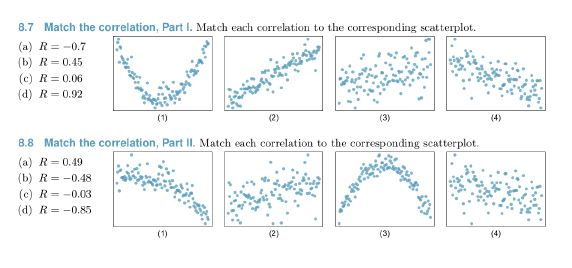
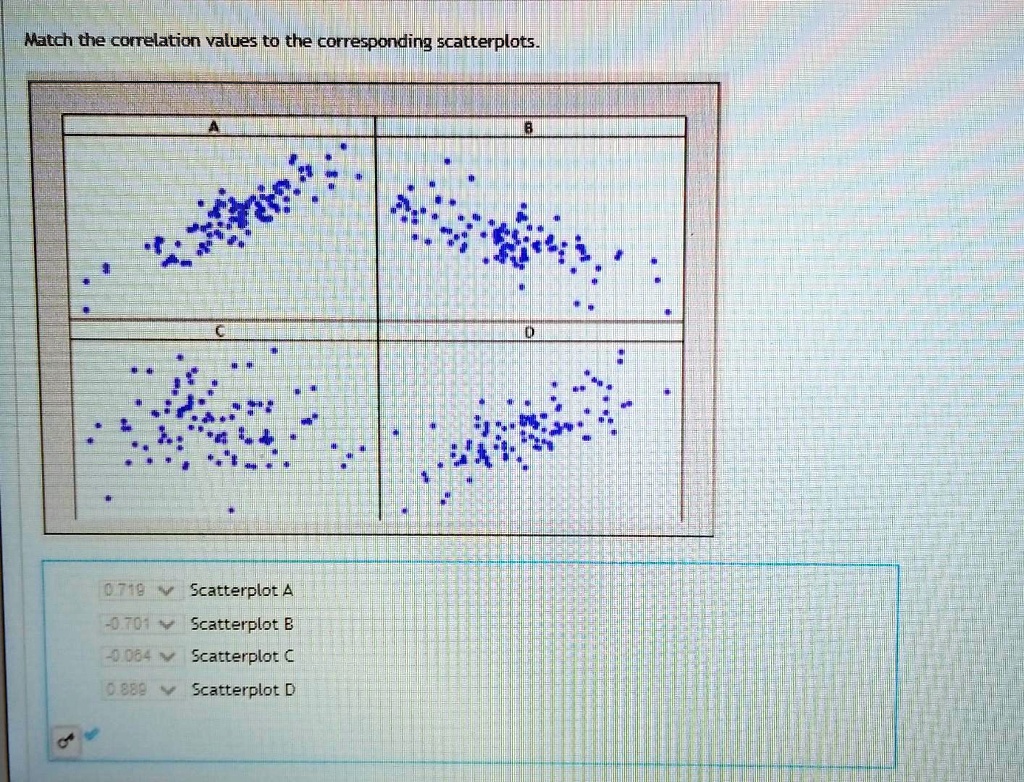
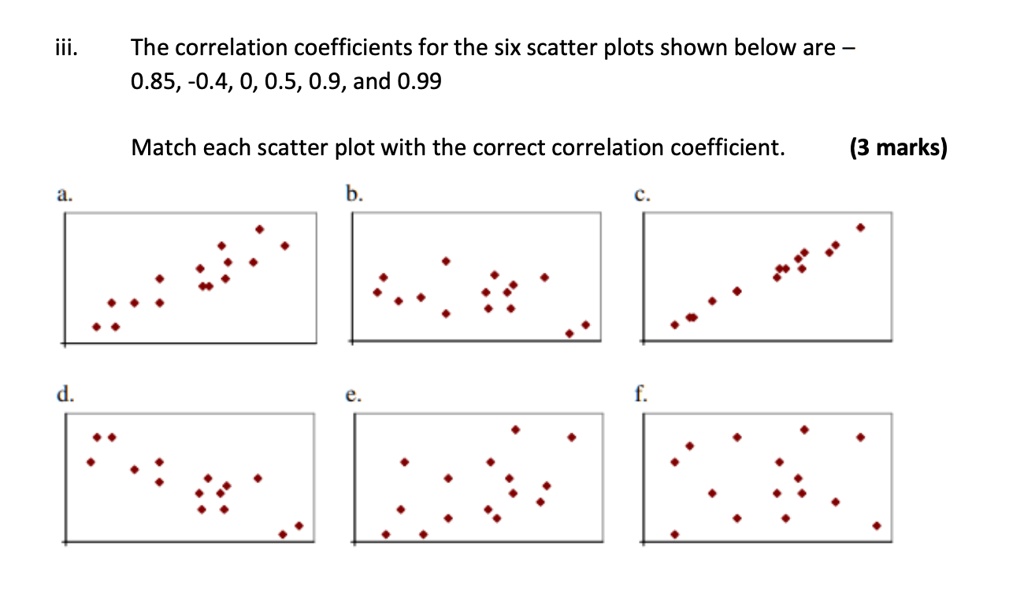
Match Each Correlation To The Corresponding Scatterplot.
So, I was helping my niece with her homework the other day – you know, the kind where you pretend you totally remember calculus when in reality you're Googling "what is a derivative?" under the table. Anyway, she’s got this math worksheet, and it’s all about scatterplots and correlations. I’m looking at these little dots scattered all over the place, and she’s asking me, "Uncle, which one shows that as my ice cream sales go up, the number of people wearing hats also goes up?"
My first thought was, "Uh, that’s a weird coincidence, kiddo, but sure, let’s find it!" And then it hit me. We’ve all seen those graphs, right? The ones that try to tell a story with dots. Sometimes the story is crystal clear, like a screaming headline. Other times, it’s more like a whisper, or even a completely nonsensical babble. That’s where understanding what a correlation is and how it looks on a scatterplot becomes super, super handy.
Think of a scatterplot as a digital canvas where we throw a bunch of data points. Each dot represents a pair of values for two different things we’re measuring. So, one dot might be (my height, my shoe size), another might be (number of hours studied, test score), or, in my niece's case, (ice cream sales, hat wearers). The magic happens when we look at the pattern these dots make. Do they go up together? Down together? Or do they just look like a sneeze exploded on the page?
This is where the concept of correlation jumps in. It’s basically a statistical measure that tells us how strongly two variables are related. Are they dancing in sync, or are they complete strangers at a party? And it’s not just about whether they move in the same direction; it’s also about how predictable that movement is. Like, if I tell you someone bought a ton of ice cream, are you pretty confident they were also rocking a fancy fedora? Or is that a total shot in the dark?
The Usual Suspects: Positive, Negative, and Zero Correlation
Let’s break down the most common types of correlation you’ll see on a scatterplot. It's like meeting the main characters in a detective novel. Each has their own personality and a predictable way of behaving.
1. The "Going Up Together" Buddy: Positive Correlation
This is the friendly one. When one variable increases, the other tends to increase too. Think about it like this: the more you practice playing the guitar, the better you usually get, right? Your guitar skills and your practice time are probably positively correlated. On a scatterplot, these guys form a pattern that slopes upwards from left to right. It's like a gentle, upward-trending hill. You can almost see the dots marching in formation towards the top right corner.
Imagine plotting "hours spent studying" on the x-axis and "exam scores" on the y-axis. As your study hours go up, your exam scores are likely to go up too. It’s not a perfect one-to-one relationship – maybe you had a bad day, or the test was surprisingly tricky – but the general trend is clear. More study time, higher score. This is your classic, textbook positive correlation.
Here’s a little secret: sometimes, people get a bit too excited about positive correlations. They see two things going up together and assume one causes the other. Remember my niece’s ice cream and hat anecdote? While it might be true that on a hot day, people buy more ice cream and wear hats (for shade!), the ice cream itself isn't causing the hat-wearing, or vice versa. It’s a third factor – the weather – that’s influencing both. This is called a spurious correlation, and it's a classic trick question in the world of data. Always be on the lookout for that hidden variable!
A strong positive correlation means the dots are tightly clustered around that upward-sloping line. A weak positive correlation means the dots are more spread out, but the upward trend is still discernible. It’s like the difference between a perfectly straight line of dancers and a slightly more chaotic, but still moving-in-the-same-direction, dance floor. You get the vibe, but it's a little less precise.
2. The "Opposite Directions" Duo: Negative Correlation
Now, this is a slightly different dynamic. When one variable goes up, the other tends to go down. Think about the relationship between "temperature outside" and "number of hot chocolate sales." As the temperature rises, the demand for hot chocolate usually plummets. These variables are negatively correlated. On a scatterplot, this pattern slopes downwards from left to right. It’s like a downhill slide, with the dots heading towards the bottom right.
Another good example: "price of a product" and "demand for that product" (assuming everything else is equal, of course!). As the price goes up, people tend to buy less. So, price on the x-axis, demand on the y-axis, and you'll likely see a downward-sloping trend. This is your classic negative correlation. They're moving in opposite directions, like two ships sailing away from each other.
Just like with positive correlations, the tightness of the dots tells us how strong the negative correlation is. A strong negative correlation means the dots are packed tightly along that downward-sloping line. A weak negative correlation means they're more scattered, but the general downward movement is still there. It's the difference between a perfectly choreographed tango where the partners are always a precise distance apart, and a more freeform dance where they're generally moving away from each other but with a lot more personal space.
It's also worth noting that sometimes, the "cause" and "effect" can be a bit blurry here too. For example, "amount of time spent exercising" and "body fat percentage." More exercise tends to lead to a lower body fat percentage, but there are many other factors involved. It’s rarely a simple, single cause. Don't fall into the trap of assuming that just because two things move in opposite directions, one must be causing the other. Correlation, as they say, is not causation. Keep that mantra handy!
3. The "Indifferent Strangers": Zero Correlation (or No Correlation)
And then there are the rebels. These variables seem to have absolutely no relationship with each other. When one goes up, the other does whatever it wants. Think about "the price of bananas in Ecuador" and "the number of car accidents in Canada." It's highly unlikely that changing the price of bananas in Ecuador is going to have any noticeable impact on car accidents in Canada. On a scatterplot, these dots will look like they've been randomly sprinkled across the graph. There's no discernible pattern, no upward slope, no downward slope. It's just… a mess. A beautiful, random mess.
This is what we call zero correlation or no correlation. It means that knowing the value of one variable gives you absolutely no predictive power for the value of the other. If you plotted "number of freckles on your face" against "your IQ," you’d probably find very little, if any, correlation. They are independent events, unrelated in any meaningful statistical way.
Sometimes, what looks like no correlation might actually be a more complex relationship, like a curve. But for the purposes of basic scatterplots and correlations, we're usually looking for those linear trends. If the dots are just all over the place with no clear direction, you're likely dealing with a zero correlation. It's the statistical equivalent of throwing your hands up and saying, "Yeah, I got nothing."
Visualizing the Relationship: Matching Scatterplots to Correlations
Okay, so how do we actually see these correlations on a scatterplot? This is where the visual detective work comes in. Imagine you have a set of scatterplots in front of you, each a unique constellation of dots. Your job is to match each one to its correct correlation description.
Scenario 1: The Upward March
You see a scatterplot where the dots are generally moving from the bottom left to the top right. They might be tightly packed, forming a clear line, or more spread out, but the direction is undeniable. This is your classic positive correlation. The steeper the upward slope, the stronger the positive correlation.
Think of it as a bunch of people climbing a hill together. Some are a bit faster, some a bit slower, but they’re all heading towards the summit. If the hill is really steep, they're all scrambling up in a hurry. If it's a gentle incline, they're strolling.
Scenario 2: The Downward Slide
On another scatterplot, the dots are predominantly moving from the top left to the bottom right. They're like a herd of sheep heading downhill. Again, they could be in a tight group or more dispersed, but the downward direction is the key. This is your negative correlation. The steeper the downward slope, the stronger the negative correlation.
Picture a ski slope. Some skiers are carving down with precision, others are a bit wobbly, but the overall movement is definitely downhill. A steep slope means they're all going down fast, while a gentle slope means a more leisurely descent.
Scenario 3: The Random Sprinkle
Then you encounter a scatterplot that looks like a painter sneezed ink onto the page. The dots are everywhere, with no discernible pattern or direction. They don't seem to lean upwards, downwards, or even sideways. This, my friends, is zero correlation, or no correlation.

Imagine a bag of confetti that's been tossed into the air. Where each piece lands is pretty much random. There's no tendency for it to all land in one corner or another. It's just… scattered.
Putting It All Together: Practice Makes Perfect
Honestly, the best way to get good at this is to look at a bunch of examples. You can find tons of scatterplot examples online, or in statistics textbooks. Try to identify the trend in each one. Does it go up, down, or nowhere in particular?
And don't forget to consider the strength of the correlation. If the dots are super close to a clear line, that's a strong correlation. If they're more spread out, but still showing a trend, it's weaker. It's all about how much you can rely on that trend to predict one variable from the other.
So, next time you’re faced with a scatterplot, don't just see a bunch of dots. See a story. Is it a story of two things growing together? Two things falling apart? Or a tale of complete indifference? Your eyes, and a little understanding of correlation, will tell you.
And hey, if you ever need to explain to your own niece why ice cream sales might correlate with hat sales, you can now tell her it's all about the weather! You're welcome.
