Lesson 7 Skills Practice Solve Systems Of Equations By Graphing

Okay, so picture this: I was trying to bake cookies the other day, right? A classic chocolate chip situation. I’d just moved into this new apartment, and of course, my oven decided to throw a tantrum. It was either too hot, like “turn your kitchen into a sauna” hot, or barely warm enough to melt butter. My baking adventures were officially on hold. I was so bummed! My roommate, bless her patient soul, finally said, “Look, maybe we need to find a way to get this oven to behave. We need a system.”
A system. That word kept popping into my head. Not just for ovens, but for life in general, you know? Like, how do you balance work, social life, and that ever-growing pile of laundry? It's all about finding that sweet spot where everything works together. And that, my friends, is pretty much what we're diving into today: solving systems of equations by graphing. Yeah, I know, the math class dread might be kicking in, but trust me, it's way less intimidating than a rogue oven and surprisingly useful.
Think of it like this: you have two (or more!) things going on, and they both have rules, or equations, that describe them. Your oven, for instance, has a "temperature setting" equation and an "actual temperature" equation. My goal was to find the point where those two lines, metaphorically speaking, crossed. Where the setting matched the reality. And when it comes to math, this "crossing point" is your solution.
So, what exactly is a system of equations? Basically, it's just a collection of two or more equations that share the same set of variables. In our cookie-baking analogy, the variables might be the dial setting and the actual oven temperature. In math land, they're usually x and y. And when we say we want to "solve" the system, we're looking for the values of those variables that make all the equations in the system true simultaneously. Pretty neat, huh?
Now, there are a few ways to tackle these systems. You can use substitution, elimination (which can feel like a magic trick sometimes!), and then, our main event today, graphing. Graphing is probably the most visual way to get your head around it. It's like drawing out the problem to see where all the pieces fit.
The Magic of the Graph
Let’s break down this "solving by graphing" thing. Imagine each equation in your system is a line on a coordinate plane. You know, with the x-axis going left and right, and the y-axis going up and down? Totally standard stuff we’ve all seen before. Each equation represents all the possible pairs of (x, y) that make that specific equation true. So, if you graph the first equation, you get a line. If you graph the second equation, you get another line.
Now, here’s the really cool part, and this is where the "system" aspect shines. If we’re looking for the values of x and y that satisfy both equations, where do you think those values would show up on our graph? That’s right! They’d be at the point where the two lines intersect. It’s like finding the exact spot where both of your oven’s "desires" meet its "reality." That single point contains the x and y values that are the solution to your entire system.
This is why graphing is so intuitive for systems. It’s a visual representation of the problem. You’re literally seeing the solution unfold before your eyes. No complicated algebraic gymnastics needed, at least not initially. Just plotting points and finding where the lines kiss.
So, How Do We Actually Do This?
Alright, enough with the analogies. Let’s get down to business. Here’s the step-by-step guide to solving a system of equations by graphing. Grab your pencil (or your stylus, if you're a fancy digital artist for math). You got this!
Step 1: Make Sure Your Equations Are Ready to Rumble.

Most of the time, you’ll want your equations in a form that’s easy to graph. The most common and helpful form is slope-intercept form, which is y = mx + b. Remember this? 'm' is the slope (how steep the line is), and 'b' is the y-intercept (where the line crosses the y-axis). If your equations aren't in this form, a little bit of algebraic rearranging (adding, subtracting, dividing) will get them there. Don't sweat it; it's just basic equation manipulation.
For example, if you have an equation like 2x + y = 5, you'd subtract 2x from both sides to get y = -2x + 5. Boom! Slope-intercept form. Easy peasy, right? It’s like prepping your ingredients before you start cooking.
Step 2: Graph the First Equation.
This is where the coordinate plane comes in. Start with the y-intercept ('b'). Plot that point on the y-axis. Then, use the slope ('m') to find at least one other point. Remember, slope is "rise over run." So, if your slope is -2/1, you'd go down 2 units and over 1 unit from your y-intercept. Keep going if you want to be super precise. Once you have a couple of points, draw a straight line through them. This line represents all the solutions to that one equation.
If you're feeling a bit rusty on graphing lines, no worries! You can always make a table of values. Pick a few x-values (like 0, 1, 2), plug them into your equation, and calculate the corresponding y-values. Then plot those (x, y) pairs and connect them. It's a foolproof way to get that line down.
Step 3: Graph the Second Equation.
Now, do the exact same thing for your second equation. Find its y-intercept and use its slope to plot its line on the same coordinate plane. This is crucial! Everything needs to be on the same graph so you can see where they meet. Don't go rogue and grab a fresh sheet of paper for the second line. That would defeat the whole purpose of finding a common solution.
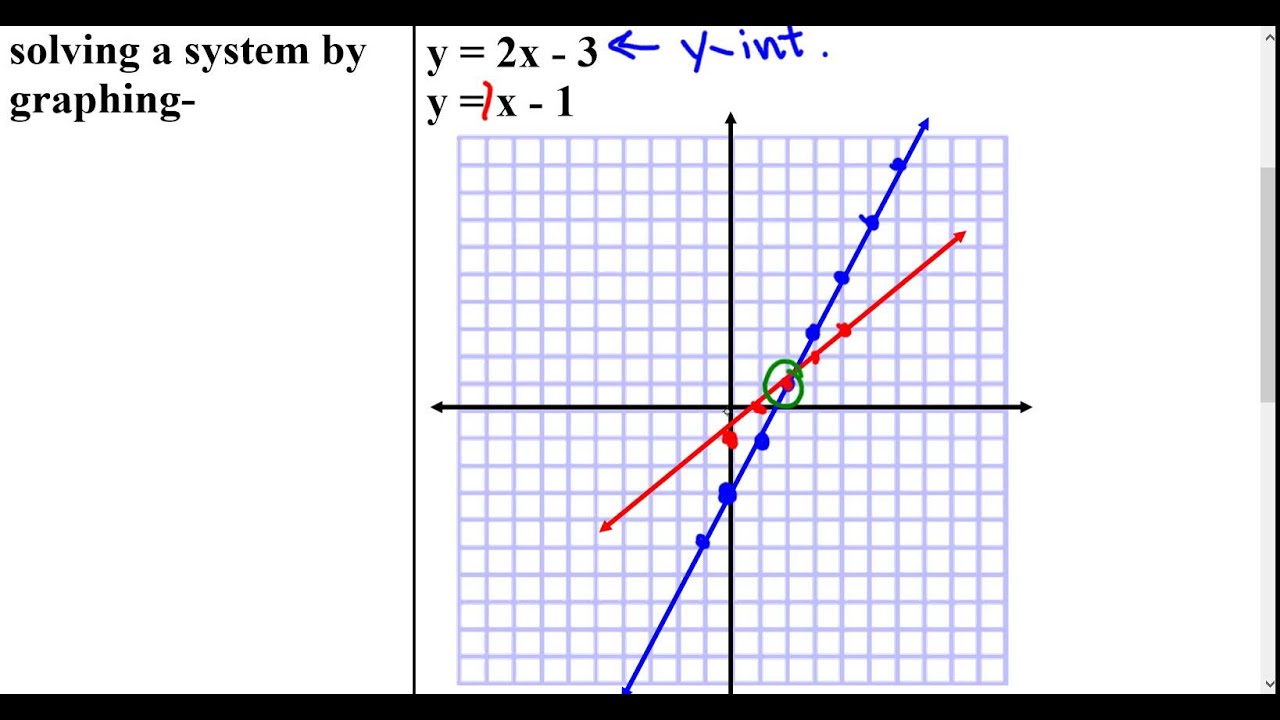
You might have different colors of pens or pencils for this step, which can be super helpful. It makes it easy to distinguish between the two lines and clearly see where they're crossing. It’s like giving each equation its own identity on the page.
Step 4: Find the Intersection Point.
Take a good, hard look at your graph. Where do the two lines cross? That single point is your jackpot! This point has an x-coordinate and a y-coordinate. These are the values that make both of your original equations true.
So, you just read off the coordinates of that intersection point. For example, if the lines cross at (3, 2), then your solution is x = 3 and y = 2. Simple as that!
Step 5: Check Your Answer.
This step is super important, and sometimes people skip it because they think they've done it right. But a quick check can save you a lot of frustration. Plug the x and y values you found from the intersection point back into both of your original equations. If you get true statements in both cases, congratulations! You’ve nailed it. If one or both equations don't work out, it means you might have made a graphing error or a calculation mistake. Go back and review your steps.
It’s like tasting your food before you serve it. You want to make sure it’s delicious and not, you know, accidentally salty instead of sweet. Checking your solution ensures your math is also delicious and correct.
When Lines Play Nice… and When They Don’t
Now, here’s where things can get a little more interesting, and sometimes a bit ironic. Not all systems of equations behave in the same way when you graph them. Most of the time, you’ll get that beautiful, single intersection point, like we’ve been talking about. But sometimes, the lines can be a bit stubborn or a bit too much of a team.
Case 1: The Unique Solution (The Most Common One)
This is the standard scenario we’ve covered. The two lines have different slopes, so they have to cross at exactly one point. This gives you a unique solution, meaning there’s only one pair of (x, y) values that satisfies both equations.
Imagine two friends walking down different paths that eventually meet at a park bench. They both arrive at the same spot, but they took different routes to get there. That park bench is your unique solution.
Case 2: No Solution (Parallel Lines)
What if the two lines you graph are perfectly parallel? This happens when the lines have the exact same slope but different y-intercepts. Think about train tracks – they go in the same direction forever and never meet. If your lines are parallel, they will never intersect. And if they never intersect, there’s no point that exists on both lines. Thus, there is no solution to this system.
It’s like having two identical recipes for cookies, but one calls for an extra tablespoon of sugar. Even though they're almost the same, the slightly different ingredient means you'll end up with slightly different cookies, and they’ll never be exactly the same at the same time. In math, this means no common ground, no common solution.
You’ll know you have no solution if, after graphing, your lines are parallel. Or, algebraically, if you end up with a statement that is clearly false, like 5 = 7. When you see that, you can confidently say, "Nope, no solution here!"
Case 3: Infinitely Many Solutions (Coincident Lines)
This is the weirdest and arguably coolest case. What happens if the two equations you’re given actually represent the exact same line? This occurs when the equations are equivalent, meaning one can be transformed into the other through algebraic manipulation. When you graph them, they will perfectly overlap, or be coincident.

If the lines are the same, then every single point on that line is a solution to both equations. Since there are infinitely many points on a line, you have infinitely many solutions. It’s like having two identical copies of the same treasure map. Every spot marked on one map is also marked on the other.
You'll see this when your graphed lines are indistinguishable. Algebraically, this often shows up as a statement that is always true, like 5 = 5. When you see that, it means any (x, y) pair that satisfies one equation will satisfy the other. Pretty mind-bending!
Why Bother With Graphing?
So, you might be wondering, "Why go through the whole process of graphing when I could just use algebra?" That’s a fair question! And honestly, for some systems, algebra might be quicker and more precise, especially if the intersection point involves fractions or decimals that are hard to read on a graph.
However, graphing gives you a fantastic visual understanding of what a system of equations is and what its solution represents. It helps you see the relationship between the equations and their common ground. It's like looking at a map versus just reading a list of directions. The map shows you the whole landscape.
Plus, for systems with non-linear equations (like parabolas or circles), graphing is often the only practical way to find approximate solutions. So, it’s a foundational skill that opens doors to more complex problems. It builds that geometric intuition that’s so important in math.
And let's be honest, sometimes, just plotting some points and drawing lines can be kind of fun and relaxing. It's a break from the abstract and a chance to get hands-on with the math. It’s a different kind of problem-solving, one that appeals to our visual learners.
So, next time you're faced with a system of equations, remember the oven, remember the cookies, and remember the power of the graph. It’s a tool that can unlock the secrets of these mathematical relationships, one intersecting point at a time. Go forth and graph!
