Lesson 7 Skills Practice Linear And Nonlinear Functions Answer Key

Alright, math explorers and curious minds! Get ready to dive headfirst into a world of numbers that's about to get a whole lot more exciting. We're talking about Lesson 7 Skills Practice: Linear and Nonlinear Functions, and let me tell you, this isn't your grandma's math class (unless your grandma is secretly a mathematical ninja, in which case, high fives!).
Think of functions like recipes. Some recipes are super straightforward, like making toast. You put in bread, you get out toast – simple, predictable, and always the same result. These are our linear functions. They're the reliable friends of the mathematical world, always showing up exactly where you expect them to.
Then you have those "experimental" recipes. You know, the ones where you throw in a pinch of this, a dash of that, and hope for the best. Maybe you're baking a cake that might rise perfectly, or it might end up looking like a delicious, albeit slightly lopsided, pancake. These are our nonlinear functions. They're the adventurous ones, full of surprises and delightful twists!
Unlocking the Secrets of Linear Functions
So, what makes a function "linear"? Imagine drawing a line on a graph. Yep, that's the essence of it! Linear functions, when graphed, create a perfect, straight line. It's like a highway with no curves, no speed bumps, just smooth sailing.
Think about your allowance. If you get $5 every week, your total savings will be a straight line upwards. After one week, you have $5. After two weeks, $10. After three weeks, $15. See? It’s predictable. For every unit you add (a week), you add a consistent amount (your $5 allowance).
This consistent addition is the superpower of linear functions. They're all about a steady rate of change. It's like a perfectly timed clock, always ticking at the same pace. No sudden jumps, no dramatic drops, just a beautiful, unwavering rhythm. This makes them super useful for everyday scenarios!
For example, if a pizza place charges a flat delivery fee plus a per-pizza cost, that's a linear function. The delivery fee is your starting point (the y-intercept, if you're feeling fancy), and the cost per pizza is your constant rate of change (the slope). No matter how many pizzas you order, the cost will increase in a nice, straight line.

Mastering linear functions is like learning to walk a straight line – it's a fundamental skill that opens up a whole world of understanding. You'll start spotting them everywhere, from your phone bill to how much water you drink each day!
Venturing into the Wonderful World of Nonlinear Functions
Now, let's talk about the rebels, the artists, the ones who dare to be different: nonlinear functions! These are the functions that don't play by the strict rules of straight lines. When you graph them, you get curves, waves, zigzags – anything but a straight shot!
Think about the growth of a plant. In the beginning, it might grow slowly, just a tiny sprout. Then, as it gets more sunlight and water, it starts to grow faster and faster. Eventually, its growth might even slow down as it reaches its full size. That's a classic nonlinear journey!
Or consider the trajectory of a basketball being shot. It goes up in a beautiful arc and then comes back down. That arc is a curve, not a straight line. It's a whole lot more interesting than just lobbing it straight up and down, right?
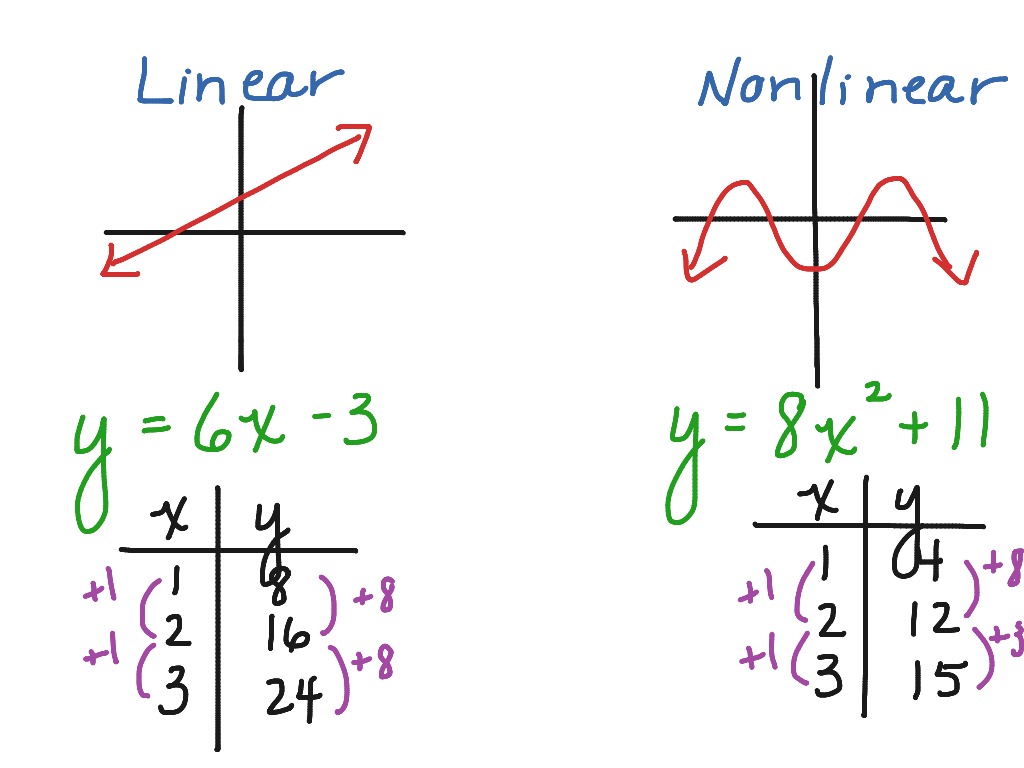
These functions are responsible for so many amazing phenomena in the real world. The speed of a roller coaster as it plunges down a hill? Nonlinear. The way sound waves travel? Nonlinear. Even the spread of a rumor in a classroom (and boy, can those spread fast!) can sometimes be modeled by nonlinear functions.
Sometimes, nonlinear functions have an accelerating or decelerating rate of change. This means they can grow or shrink at an increasing or decreasing pace. It’s like a snowball rolling down a hill – it starts small but picks up speed and size incredibly quickly!
The beauty of nonlinear functions is their ability to capture complexity. They can describe situations where things aren't simply adding up at a steady rate. They allow us to model the messy, beautiful, and often unpredictable aspects of our world with remarkable accuracy.
The Answer Key: Your Magical Compass
Now, you might be wondering, "Okay, this sounds cool, but how do I actually do this stuff?" That's where the Lesson 7 Skills Practice: Linear and Nonlinear Functions Answer Key swoops in like a superhero! Think of it as your trusty map and compass for navigating the world of these functions.
This answer key is your secret weapon. It’s the friendly guide that says, "Psst, you got this!" It's there to help you check your work, understand where you might have taken a slight detour, and celebrate those moments when you nail it.

When you're working through the practice problems, don't be afraid to consult the answer key. It's not about cheating; it's about learning and building confidence. Imagine you're trying to assemble a complicated LEGO set. The instructions (your practice problems) are there, and the completed model (the answer key) shows you what it's supposed to look like.
You'll see examples of how linear functions are solved, revealing those perfectly straight lines. You'll also see how nonlinear functions create those fascinating curves and bends. It’s like watching a master artist at work, and you get to learn their techniques!
The key isn't just about getting the right answer; it's about understanding why it's the right answer. The more you use the answer key as a learning tool, the more you'll start to see the patterns yourself. You'll begin to anticipate the outcomes and develop that intuitive sense for whether a function is linear or nonlinear.
Think of it as having a wise tutor available 24/7. It patiently shows you the steps, confirms your brilliant insights, and gently nudges you in the right direction when needed. It’s designed to make you feel empowered and successful!
Putting It All Together: The Fun Part!
So, why are we even bothering with all this linear and nonlinear magic? Because it helps us understand the world around us! From planning a budget to predicting the weather, these functions are the silent architects of our reality.
When you're doing the Lesson 7 Skills Practice, imagine you're a detective. You're looking at clues (the numbers and equations) and trying to figure out the nature of the "suspect" (the function). Is it a predictable, straight-line-type character, or a wild, unpredictable curveball?
Embrace the challenge! Every problem you solve is like leveling up in a video game. You're gaining new skills, unlocking new abilities, and becoming a mathematical superhero in your own right.
Don't be intimidated by the terms. Linear just means straight, and nonlinear means not straight. That’s it! The "functions" part just means there's a relationship between input and output, like a machine that takes something in and gives something else out.
So, go forth and conquer! Use your Lesson 7 Skills Practice: Linear and Nonlinear Functions Answer Key as your trusty sidekick. Dive into the straightforward elegance of linear functions and marvel at the captivating complexity of nonlinear ones. You've got this, and it's going to be a wonderfully mathematical adventure!
