Lesson 5 Homework Practice Graph A Line Using Intercepts

Ah, Lesson 5 Homework Practice: Graph a Line Using Intercepts. Just saying those words out loud feels like a gentle, perhaps slightly mischievous, nudge from your math teacher. You know the kind. The one who smiles ever-so-sweetly when they assign something that sounds… dare I say it… fun? Well, maybe not everyone’s cup of tea, but let’s lean into it, shall we?
Think of it as a treasure hunt, but instead of buried gold, we’re digging for points on a graph. And the map? It's all about these magical things called intercepts. They’re like secret passwords that unlock the secrets of drawing a straight line.
Now, I know what you’re thinking. "Intercepts? Is that some fancy new coffee shop near campus?" Nope, my friends. While a good latte can definitely help with homework, these intercepts are purely mathematical. And surprisingly, they’re not as intimidating as they sound.
Let’s break down the main players in this graphing adventure. We have the y-intercept. This is where your line decides to say "hello" to the vertical axis, the one that goes up and down like a very determined elevator. It’s the point where your line crosses the y-axis.
And then, there’s its equally important cousin, the x-intercept. This is where the line has a little rendezvous with the horizontal axis, the one that stretches out left and right like a very long, very straight road. It’s the point where your line crosses the x-axis.
So, how do we find these elusive intercept points? It’s surprisingly straightforward. For the y-intercept, we set our beloved x variable to zero. Think of it as giving x a vacation. When x is on break, what does y do? It gives us the height at which our line meets the y-axis.
And for the x-intercept? You guessed it! We give the y variable a little break by setting it to zero. When y is chilling, what does x become? It tells us how far along the x-axis our line decides to show up.

Once you’ve successfully located these two special points – your trusty (0, y-intercept) and your adventurous (x-intercept, 0) – the rest is a piece of cake. Or, you know, a piece of graph paper. You simply plot these two points. Imagine them as two bright little stars on your coordinate plane.
Then, the grand finale! You grab a ruler. Yes, an actual ruler! This is where your childhood ruler obsession might finally come in handy. You connect those two points with a straight line. And poof! You’ve just graphed a line using intercepts. How cool is that?
It’s like having a secret shortcut. Instead of painstakingly finding a bunch of random points and hoping they line up, you’re given two golden tickets that automatically build your line for you. It’s efficiency at its finest, and honestly, I’m here for it.
Now, I have an unpopular opinion, but bear with me. Sometimes, this method is even easier than plugging in a bunch of x-values and calculating the corresponding y-values. I know, I know. Blasphemy! But hear me out. Two calculations, two points, one line. It's a pretty sweet deal.

Think about it. You have an equation like, say, 2x + 3y = 6. To find the y-intercept, set x = 0: 2(0) + 3y = 6. This simplifies to 3y = 6, so y = 2. Boom! Your y-intercept is at (0, 2).
Now, for the x-intercept. Set y = 0: 2x + 3(0) = 6. This becomes 2x = 6, so x = 3. Ta-da! Your x-intercept is at (3, 0).
So, you’ve got your two points: (0, 2) and (3, 0). You mark them on your graph. Then, you draw a line connecting them. It’s almost… therapeutic. A quiet moment of mathematical creation.
It’s a shame that sometimes these simpler methods get overshadowed. We get so caught up in the complexity, we forget the beauty of a direct approach. This lesson is a gentle reminder that math can be elegant. It can be a straightforward path, not always a winding, confusing maze.
![🔴 Grade 8 – Chapter 3 – Lesson 5 [[ Graph a Line Using Intercepts ]] 🔴](https://i.ytimg.com/vi/rxlbrRNyZhI/maxresdefault.jpg)
And let’s be honest, the satisfaction of drawing a perfect line with just two points is immense. It’s like solving a mini-puzzle and feeling like a graphing ninja. You’ve conquered the coordinate plane, one intercept at a time.
So, the next time you see "Graph a Line Using Intercepts" staring back at you from your homework, don't groan. Smile. Or at least, a small, knowing smirk. Because you know the secret. You know how to find those magical points and unleash the power of the straight line.
It’s a skill that will serve you well. Beyond the classroom, understanding how lines work and how to represent them is pretty fundamental. And doing it this way? It’s efficient, it's clear, and it’s, dare I say it again, kind of delightful.
So go forth, my friends. Embrace the intercepts. Plot them with confidence. Draw those lines with flair. And remember, sometimes, the easiest way is the most rewarding way. Especially when it involves rulers and a satisfyingly straight mark on paper.
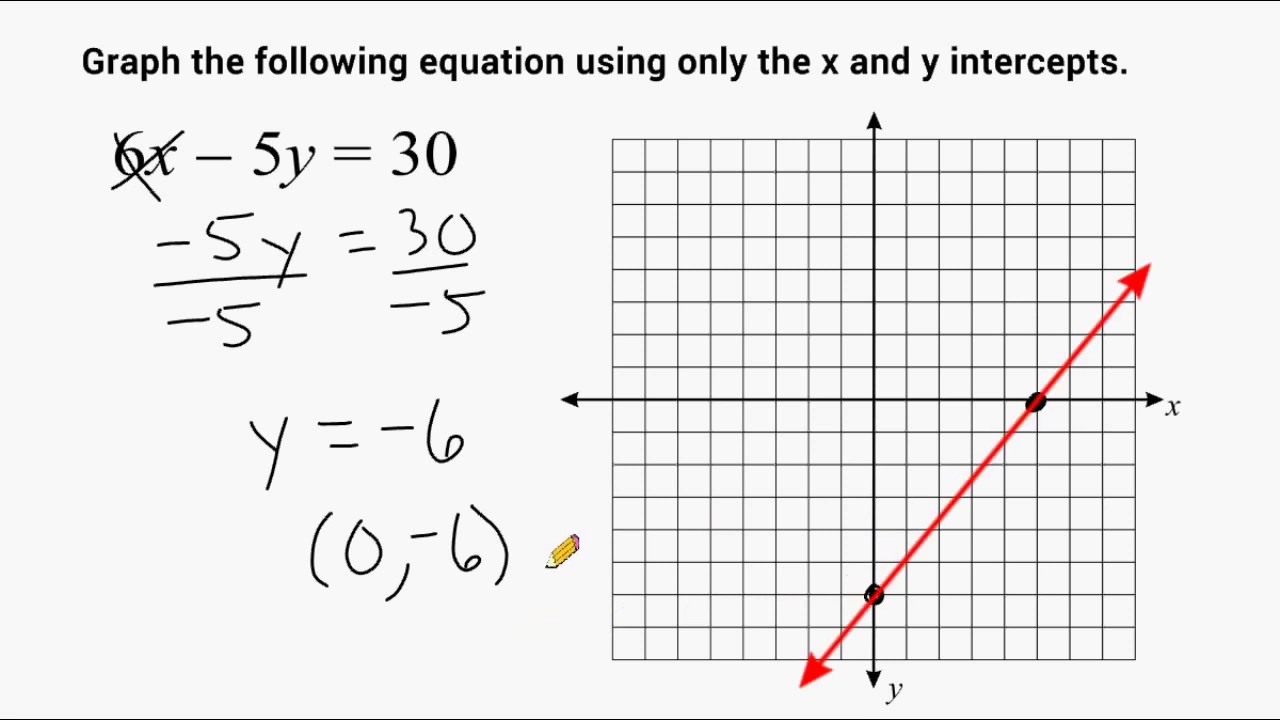
This lesson is less about drudgery and more about discovery. It’s about finding the quick path to understanding. It’s about seeing the forest and the trees, but in this case, the trees are just two very important points.
Think of it as your mathematical superpower. You can look at an equation and immediately see where it will hit the main axes. It’s like having X-ray vision for graphs. Pretty neat, right?
And when you’re done, and your line is perfectly drawn, take a moment. Appreciate the simplicity. Appreciate the power of the intercept. You’ve earned it.
It’s a small victory, perhaps, but in the grand scheme of things, mastering these building blocks of algebra is what it’s all about. So, thank you, Lesson 5 Homework Practice: Graph a Line Using Intercepts. You’re not so bad after all.
