Lesson 4 Problem Solving Practice Proportional And Nonproportional Relationships

Ever feel like math can be a bit of a puzzle? Well, get ready to have some fun! We're diving into something super cool called Lesson 4 Problem Solving Practice. And guess what? It's all about figuring out how things are connected. Think of it like being a detective, but for numbers and relationships!
Now, there are two main types of connections we're going to explore. The first one is called a proportional relationship. This is like when you're baking cookies. If you double the recipe, you need to double all the ingredients. It's a nice, steady, predictable relationship. Everything stays in line. If one thing goes up, the other goes up by the exact same factor. It's like a perfect dance – two steps forward, two steps forward. There are no weird surprises here!
Imagine you're buying apples. If one apple costs $1, then two apples cost $2, and ten apples cost $10. See how that works? It's super straightforward. The cost is always proportional to the number of apples. This is the kind of relationship that makes you feel really in control, like you've got the whole system figured out. It’s like a smooth, downhill bike ride – you just keep rolling along!
Then, we have the other kind, the nonproportional relationship. This is where things can get a little more interesting, and dare I say, exciting! With a nonproportional relationship, things don't always scale up perfectly. There might be a starting fee, or some other twist that throws off the neat proportionality. It's not a bad thing, though! It just means you have to pay a little more attention. It's like a rollercoaster – sometimes you go up steadily, and then, WHOOSH, things change!
Think about ordering pizza. You might have a base delivery fee, say $5. Then, each pizza is an extra $10. So, one pizza is $15 total ($5 delivery + $10 pizza). Two pizzas are $25 total ($5 delivery + $20 in pizzas). Notice how the cost didn't just double when you doubled the pizzas? That initial $5 delivery fee throws it off. That's the nonproportional magic at play! It adds a layer of complexity that makes problem-solving more of a brain-tickler.

The really awesome part about Lesson 4 Problem Solving Practice is that it helps you get really good at spotting these different types of relationships. You'll learn to look at a situation and say, "Aha! This looks like a proportional scenario!" or "Hmm, this one's got a bit of a nonproportional flavor." It’s like developing a superpower for understanding how the world works, one math problem at a time.
Why is this so entertaining, you ask? Because it’s all about making sense of things! Math isn't just about memorizing formulas. It's about thinking critically and creatively. This lesson turns you into a mathematical explorer. You get to investigate, observe, and draw conclusions. It’s like a treasure hunt where the treasure is understanding!
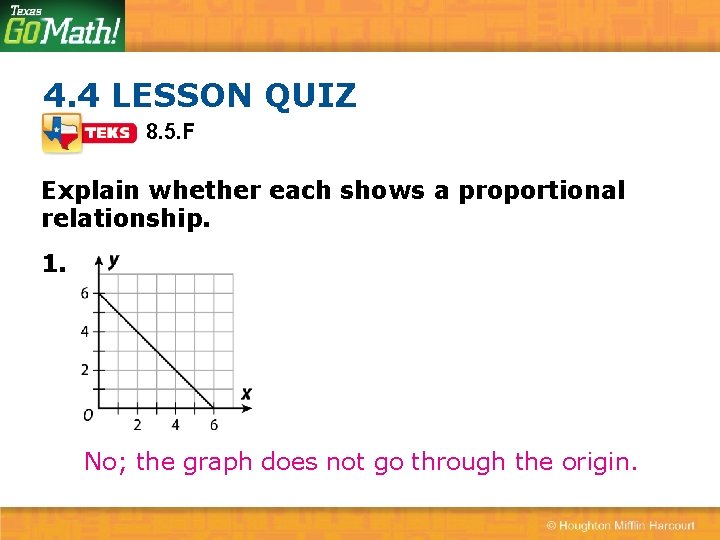
Let's say you're trying to figure out the best way to save money. If you save $10 a week, that's a proportional relationship. Your savings go up by $10 every week. Easy peasy. But what if you get a $50 bonus one week? That throws your neat $10-a-week pattern off, creating a temporary nonproportional bump in your savings. Understanding these differences helps you make smarter decisions, whether it's about money, planning a trip, or even figuring out how much paint you need for a project.
The Problem Solving Practice part is where you really get to shine. You're not just learning the concepts; you're using them. You'll be presented with real-world scenarios, and your job is to break them down. It’s like having a set of tools and then being given a bunch of interesting things to build. You get to decide which tool is best for the job. Do you need the steady, reliable hammer of proportionality, or the more adaptable wrench of nonproportionality?

What makes it special? It’s the feeling of accomplishment when you crack a tough problem. It’s that "aha!" moment when the numbers suddenly click. It's about building confidence. You start seeing math not as a scary subject, but as a powerful tool for understanding and navigating the world around you. It’s like learning to ride a bike – at first, it might seem wobbly, but with practice, you’re cruising!
Think about sports. If a player scores 2 points per game, that's proportional. If they score 2 goals in the first game and 3 in the second, that's nonproportional. Analyzing these patterns helps coaches understand performance and make better strategies. Lesson 4 gives you the skills to do that kind of analysis yourself!
So, if you're looking for a way to sharpen your mind, become a better problem-solver, and maybe even have a little bit of fun along the way, then definitely check out this Lesson 4 Problem Solving Practice. It's a fantastic journey into the fascinating world of proportional and nonproportional relationships, and you might just surprise yourself with how much you enjoy it!
